有关微信小程序
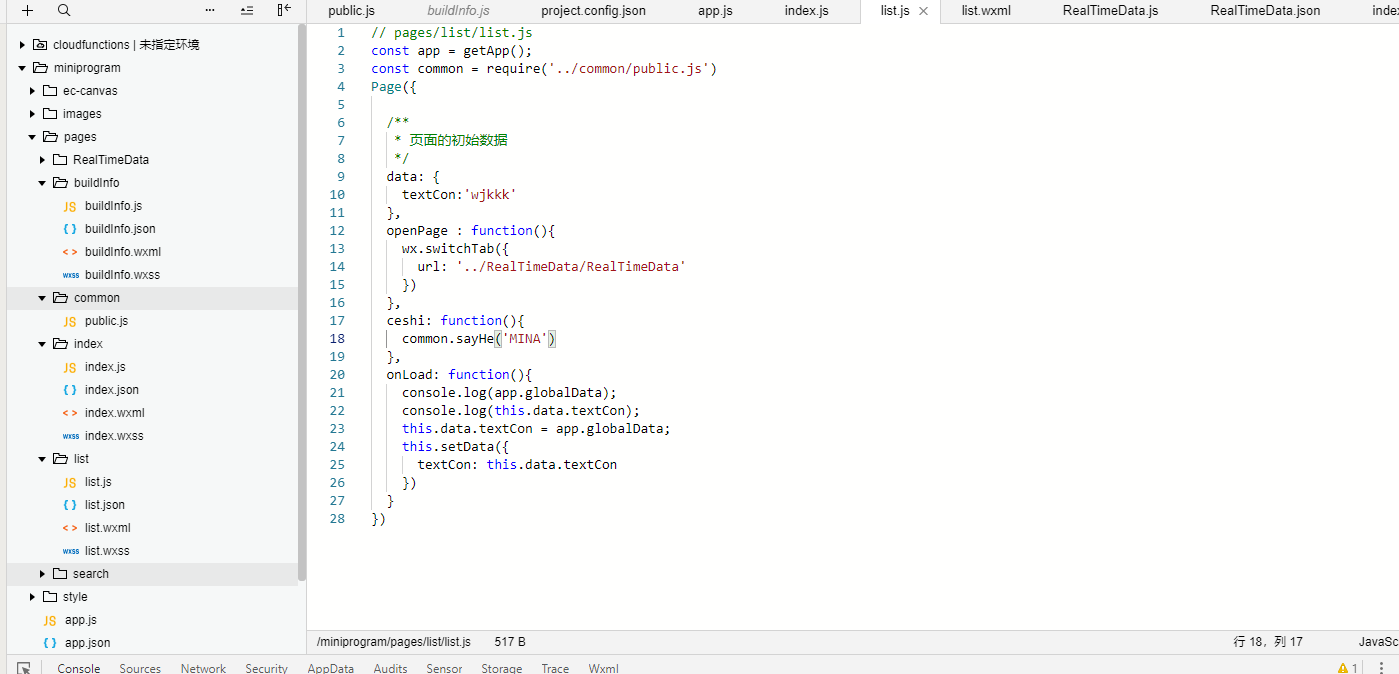
每个页面都要在app.json中配置
)
有关微信小程序的更多相关文章
- 微信小程序开发心得
微信小程序也已出来有一段时间了,最近写了几款微信小程序项目,今天来说说感受. 首先开发一款微信小程序,最主要的就是针对于公司来运营的,因为,在申请appid(微信小程序ID号)时候,需要填写相关的公司 ...
- 微信小程序体验(2):驴妈妈景区门票即买即游
驴妈妈因为出色的运营能力,被腾讯选为首批小程序内测单位.驴妈妈的技术开发团队在很短的时间内完成了开发任务,并积极参与到张小龙团队的内测问题反馈.驴妈妈认为,移动互联网时代,微信是巨大的流量入口,也是旅 ...
- 微信小程序(微信应用号)组件讲解
这篇文章主要讲解微信小程序的组件. 首先,讲解新建项目.现在有句话:招聘三天以上微信小程序开发,这个估计只能去挖微信的工程师了.技术新,既然讲解,那我们就从开始建项目讲解. 打开微信web开发者工具, ...
- 神技!微信小程序(应用号)抢先入门教程(附最新案例DEMO-豆瓣电影)持续更新
微信小程序 Demo(豆瓣电影) 由于时间的关系,没有办法写一个完整的说明,后续配合一些视频资料,请持续关注 官方文档:https://mp.weixin.qq.com/debug/wxadoc/de ...
- 通过微信小程序看前端
前言 2016年9月22日凌晨,微信官方通过“微信公开课”公众号发布了关于微信小程序(微信应用号)的内测通知.整个朋友圈瞬间便像炸开了锅似的,各种揣测.介绍性文章在一夜里诞生.而真正收到内测邀请的公众 ...
- 快速了解微信小程序的使用,一个根据小程序的框架开发的todos app
微信官方已经开放微信小程序的官方文档和开发者工具.前两天都是在看相关的新闻来了解小程序该如何开发,这两天官方的文档出来之后,赶紧翻看了几眼,重点了解了一下文档中框架与组件这两个部分,然后根据简易教程, ...
- 来自于微信小程序的一封简讯
9月21晚间,微信向部分公众号发出公众平台-微信应用号(小程序)的内测邀请,向来较为低调的微信在这一晚没人再忽视它了. 来自个人博客:Damonare的个人博客 一夜之间火了的微信应用号你真的知道吗? ...
- 微信小程序前端源码逻辑和工作流
看完微信小程序的前端代码真的让我热血沸腾啊,代码逻辑和设计一目了然,没有多余的东西,真的是大道至简. 废话不多说,直接分析前端代码.个人观点,难免有疏漏,仅供参考. 文件基本结构: 先看入口app.j ...
- 微信小程序初探
做为码农相信大家最近肯定都会听到微信小程序,虽然现阶段还没有正式开放注册,但大家可以还是可以开发测试. 到微信的WIKI(http://mp.weixin.qq.com/wiki?t=resource ...
- 【微信小程序开发】之如何获取免费ssl证书【图文步骤】
微信小程序要求所有网络请求都走ssl加密,因此我们开发服务端接口需要配置为https 这篇文章介绍一下如何 在 startssl 申请一个免费的ca证书. 1. 打开网站 https://www.s ...
随机推荐
- [vagrant]第一次安装添加box出现问题汇总
1.本地文件要加全文件名和协议file:/// 2.The box failed to unpackage properly. Please verify that the box file you' ...
- centos7 安装vsftpd的步骤
感觉非常坑,依照网上说的没一个都測试了,可一直都报错. 不断的又一次安装不下10次,最后一次最终測试出了正确的方法. #官网配置说明## https://security.appspot.com/vs ...
- HDU 5392 BC #51
就是求最大公倍数,但要用分解质因子求. 自己写的WA到爆.... #include<iostream> #include<stdio.h> #include<math.h ...
- POJ 1128 Frame Stacking(拓扑排序·打印字典序)
题意 给你一些矩形框堆叠后的鸟瞰图 推断这些矩形框的堆叠顺序 每一个矩形框满足每边都至少有一个点可见 输入保证至少有一个解 按字典序输出全部可行解 和上一题有点像 仅仅是这个要打印全部的可行 ...
- 安装 KB2844286 导致SharePoint 2010 XSLT web part 显示出现错误
上周末给Windows 打完补丁后,周一在通过From SharePoint的方式插入图片时,出现了如下错误: Unable to display this Web Part. To troubles ...
- 用CSS3实现带有阴影效果和颜色渐变的按钮
这里讲下如何利用css3里的两个新属性 box-shadow和transition来实现如下所示的带有阴影和颜色渐变效果的按钮(下面这个只是图片:本想直接在这个页面下嵌html的,,试了后发现有些cs ...
- oc37--类工厂方法
// // Person.h #import <Foundation/Foundation.h> @interface Person : NSObject @property int ag ...
- c# winform 多条件查找 外加网络人才回答
浮生 Э 2012-11-22 c# winform 多条件查找 20 我现在有2个textbox 一个是用户名,另一个是电话 现在想对这两个进行条件查找datagridview里的数据 s ...
- nyoj--1100--WAJUEJI which home strong!(bfs)
WAJUEJI which home strong! 时间限制:1000 ms | 内存限制:65535 KB 难度:2 描述 在一个山沟里,姐弟俩同时考上了大学.但由于家里拮据,所以这并不是什么 ...
- 【转】UINavigationController 直接返回到第一级目录
原文网址:http://blog.csdn.net/justinjing0612/article/details/7360852 [self.navigationController popViewC ...
