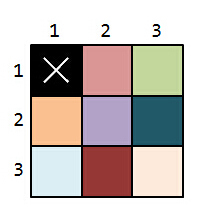图解hdu5301Buildings
这个题就是给出一个大矩形n*m。当中有个1*1的小格子不能被占用,然后要你用非常多小矩形去填满。问小矩形的最小最大面积是多少。
显然小矩形必定是1*x的最好,毕竟i*x,若i>1则还是能够拆成非常多1*x。
显然若没有那个被占用的格子。那么答案就是min(n,m)+1>>1。
当考虑这个格子的时候,我们把矩形调整下,保证n<m,然后就非常显然,除了被格子占用的那一列j,其它的列k,不管k<j还是k>j必定至少有一个还是用(min(n,m)+1>>1)*1的矩形去竖着填最好,那么考虑仅仅有一个被这样的方案填了,那么还有一个肯定要用这样的方案或者考虑横着填。
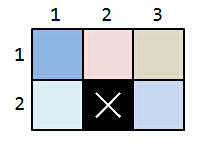
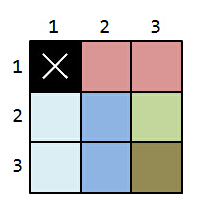
这两种情况画出来就是这样:
上面的图,同一种颜色代表由相同的1*x的小矩形组成的部分,第一张图的左边是横着插。第二张图右边都是竖着插。
于是就能够非常显然的推出式子。另外再单独考虑n=m,且都是奇数,切被占格子在正中间的情况就可以。
#include<map>
#include<string>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<vector>
#include<iostream>
#include<algorithm>
#include<bitset>
#include<climits>
#include<list>
#include<iomanip>
#include<stack>
#include<set>
using namespace std;
int a[10];
int main()
{
int n,m,x,y;
while(cin>>n>>m>>x>>y)
{
if(n==m&&(n&1)&&x==n+1>>1&&y==x)
{
cout<<(n+1>>1)-1<<endl;
continue;
}
if(n>m)
{
swap(n,m);
swap(x,y);
}
a[0]=x-1;
a[1]=n-x;
a[2]=y;
a[3]=m-y+1;
a[4]=n+1>>1;
int ans=max(a[4],min(max(a[0],a[1]),min(a[2],a[3])));
cout<<ans<<endl;
}
}
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 1237 Accepted Submission(s): 335
The floor is represented in the ground plan as a large rectangle with dimensions n×m,
where each apartment is a smaller rectangle with dimensions a×b located
inside. For each apartment, its dimensions can be different from each other. The number a and b must
be integers.
Additionally, the apartments must completely cover the floor without one 1×1 square
located on (x,y).
The apartments must not intersect, but they can touch.
For this example, this is a sample of n=2,m=3,x=2,y=2.
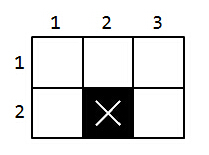
To prevent darkness indoors, the apartments must have windows. Therefore, each apartment must share its at least one side with the edge of the rectangle representing the floor so it is possible to place a window.
Your boss XXY wants to minimize the maximum areas of all apartments, now it's your turn to tell him the answer.
For each testcase, only four space-separated integers, n,m,x,y(1≤n,m≤108,n×m>1,1≤x≤n,1≤y≤m).
2 3 2 2
3 3 1 1
1
2HintCase 1 :
You can split the floor into five 1×1 apartments. The answer is 1. Case 2:
You can split the floor into three 2×1 apartments and two 1×1 apartments. The answer is 2.
If you want to split the floor into eight 1×1 apartments, it will be unacceptable because the apartment located on (2,2) can't have windows.
图解hdu5301Buildings的更多相关文章
- 图解CSS3制作圆环形进度条的实例教程
圆环形进度条制作的基本思想还是画出基本的弧线图形,然后CSS3中我们可以控制其旋转来串联基本图形,制造出部分消失的效果,下面就来带大家学习图解CSS3制作圆环形进度条的实例教程 首先,当有人说你能不能 ...
- 《图解HTTP》读书笔记
目前国内讲解HTTP协议的书是在太少了,记忆中有两本被誉为经典的书<HTTP权威指南>与<TCP/IP详解,卷1>,但内容晦涩难懂,学习难度较大.其实,HTTP协议并不复杂,理 ...
- [PostgreSQL] 图解安装 PostgreSQL
图解安装 PostgreSQL [博主]反骨仔 [原文地址]http://www.cnblogs.com/liqingwen/p/5894462.html 序 园友的一篇<Asp.Net Cor ...
- 图解ios程序生命周期
图解ios程序生命周期 应用程序启动后状态有Active.Inactive.Background.Suspended.Not running这5种状态,几种状态的转换见下图: 在AppDelegate ...
- 【用xocde5打包 在IOS7以下也能显示无默认gloss 效果 图解】
图解,只需要这几个地方修改以下就好了,看不懂的话,请留言 完毕:记着clean 以下项目文件
- Python开发工具PyCharm个性化设置(图解)
Python开发工具PyCharm个性化设置,包括设置默认PyCharm解析器.设置缩进符为制表符.设置IDE皮肤主题等,大家参考使用吧. JetBrains PyCharm Pro 4.5.3 中文 ...
- (转)Eclipse和MyEclipse安装和使用git(egit)图解笔记
Eclipse.MyEclipse使用git插件(egit)图解 (转)原文来自:http://www.xuebuyuan.com/446322.html 在开发Java.JavaEE等相关程序时,我 ...
- C#温故知新:《C#图解教程》读书笔记系列
一.此书到底何方神圣? 本书是广受赞誉C#图解教程的最新版本.作者在本书中创造了一种全新的可视化叙述方式,以图文并茂的形式.朴实简洁的文字,并辅之以大量表格和代码示例,全面.直观地阐述了C#语言的各种 ...
- 字符串模式匹配之KMP算法图解与 next 数组原理和实现方案
之前说到,朴素的匹配,每趟比较,都要回溯主串的指针,费事.则 KMP 就是对朴素匹配的一种改进.正好复习一下. KMP 算法其改进思想在于: 每当一趟匹配过程中出现字符比较不相等时,不需要回溯主串的 ...
随机推荐
- [学习笔记]HTTP协议
转自:www.cnblogs.com/li0803/archive/2008/11/03/1324746.html Author :Jeffrey 引言 HTTP是一个属于应用层的面向对象的协议,由于 ...
- PostgreSQL备份与还原
物理备份:整个数据库的数据目录及文件做备份:备份整个数据库的文件系统. 物理恢复:恢复整个数据库的文静系统. 物理备份方法: 开启归档 select pg_start_backup('backup—— ...
- dedecms后台登录,与后台界面去除多于的样式
http://jingyan.baidu.com/article/597035520f4edc8fc00740f7.html
- objc_clear_deallocating 与弱引用
void *objc_destructInstance(id obj){ if (obj) { Class isa_gen = _object_getClass(obj); class_t *isa ...
- HDU-2045 不容易系列之(3)—— LELE的RPG难题 找规律&递推
题目链接:https://cn.vjudge.net/problem/HDU-2045 找规律 代码 #include <cstdio> long long num[51][2]; int ...
- whatis---查询一个命令执行什么功能
whatis命令是用于查询一个命令执行什么功能,并将查询结果打印到终端上. whatis命令在用catman -w命令创建的数据库中查找command参数指定的命令.系统调用.库函数或特殊文件名.wh ...
- 20180929 北京大学 人工智能实践:Tensorflow笔记06
入戏 需要修改成如下: (完)
- vue2.0学习教程
十分钟上手-搭建vue开发环境(新手教程)https://www.jianshu.com/p/0c6678671635 如何在本地运行查看github上的开源项目https://www.jianshu ...
- Cocos2d-x 3.0 Schedule in Node
***************************************转载请注明出处:http://blog.csdn.net/lttree************************** ...
- POJ 3150 Cellular Automaton(矩阵高速幂)
题目大意:给定n(1<=n<=500)个数字和一个数字m,这n个数字组成一个环(a0,a1.....an-1).假设对ai进行一次d-step操作,那么ai的值变为与ai的距离小于d的全部 ...