深入解析Dropout——基本思想：以概率P舍弃部分神经元，其它神经元以概率q=1-p被保留，舍去的神经元的输出都被设置为零

深度学习网络大杀器之Dropout——深入解析Dropout

 转自：https://yq.aliyun.com/articles/68901

摘要： 本文详细介绍了深度学习中dropout技巧的思想，分析了Dropout以及Inverted Dropout两个版本，另外将单个神经元与伯努利随机变量相联系让人耳目一新。

过拟合是深度神经网（DNN）中的一个常见问题：模型只学会在训练集上分类，这些年提出的许多过拟合问题的解决方案；其中dropout具有简单性并取得良好的结果：

Dropout

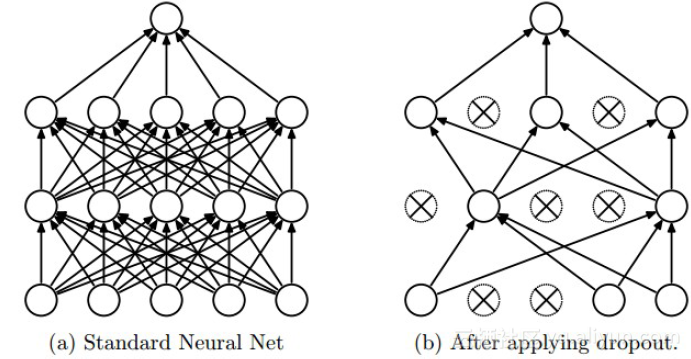
上图为Dropout的可视化表示，左边是应用Dropout之前的网络，右边是应用了Dropout的同一个网络。

Dropout的思想是训练整体DNN，并平均整个集合的结果，而不是训练单个DNN。DNNs是以概率P舍弃部分神经元，其它神经元以概率q=1-p被保留，舍去的神经元的输出都被设置为零。

引述作者：

在标准神经网络中，每个参数的导数告诉其应该如何改变，以致损失函数最后被减少。因此神经元元可以通过这种方式修正其他单元的错误。但这可能导致复杂的协调，反过来导致过拟合，因为这些协调没有推广到未知数据。Dropout通过使其他隐藏单元存在不可靠性来防止共拟合。

简而言之：Dropout在实践中能很好工作是因为其在训练阶段阻止神经元的共适应。

Dropout如何工作

Dropout以概率p舍弃神经元并让其它神经元以概率q=1-p保留。每个神经元被关闭的概率是相同的。这意味着：

假设：

h(x)=xW+b，d_i维的输入x在d_h维输出空间上的线性投影；

a(h)是激活函数

在训练阶段中，将假设的投影作为修改的激活函数：

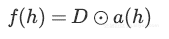
其中D=(X₁,...,X_dh)是d_h维的伯努利变量Xi，伯努利随机变量具有以下概率质量分布：

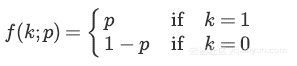
其中k是可能的输出。

将Dropout应用在第i个神经元上：

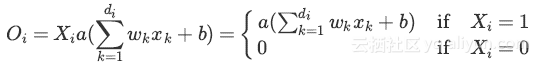
其中P(X_i=0)=p

由于在训练阶段神经元保持q概率，在测试阶段必须仿真出在训练阶段使用的网络集的行为。

为此，作者建议通过系数q来缩放激活函数：

训练阶段：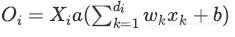

测试阶段：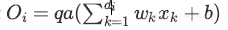

Inverted Dropout

与dropout稍微不同。该方法在训练阶段期间对激活值进行缩放，而测试阶段保持不变。

倒数Dropout的比例因子为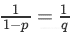，因此：

训练阶段：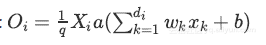

测试阶段：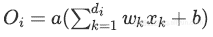

Inverted Dropout是Dropout在各种深度学习框架实践中实现的，因为它有助于一次性定义模型，并只需更改参数（保持/舍弃概率）就可以在同一模型上运行训练和测试过程。

一组神经元的Dropout

n个神经元的第h层在每个训练步骤中可以被看作是n个伯努利实验的集合，每个成功的概率等于p。

因此舍弃部分神经元后h层的输出等于：

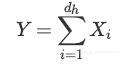
因为每一个神经元建模为伯努利随机变量，且所有这些随机变量是独立同分布的，舍去神经元的总数也是随机变量，称为二项式：

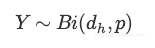
n次尝试中有k次成功的概率由概率质量分布给出：

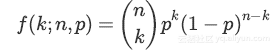
当使用dropout时，定义了一个固定的舍去概率p，对于选定的层，成比例数量的神经元被舍弃。

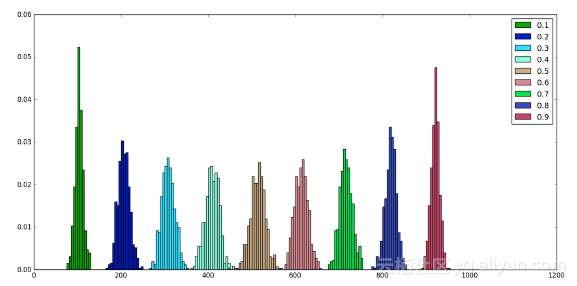
从上图可以看出，无论p值是多少，舍去的平均神经元数量均衡为np：

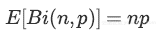
此外可以注意到，围绕在p = 0.5值附近的分布是对称。

Dropout与其它正则化

Dropout通常使用L2归一化以及其他参数约束技术。正则化有助于保持较小的模型参数值。

L2归一化是损失的附加项，其中λ是一种超参数、F(W;x)是模型以及ε是真值y与和预测值y^之间的误差函数。

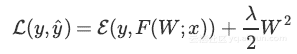
通过梯度下降进行反向传播，减少了更新数量。

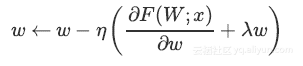
Inverted Dropout和其他正则化

由于Dropout不会阻止参数增长和彼此压制，应用L2正则化可以起到作用。

明确缩放因子后，上述等式变为：

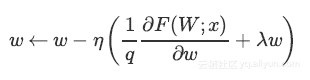
可以看出使用Inverted Dropout，学习率是由因子q进行缩放 。由于q在[0,1]之间，η和q之间的比例变化：

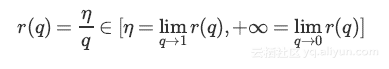
将q称为推动因素，因为其能增强学习速率，将r(q)称为有效的学习速率。

有效学习速率相对于所选的学习速率而言更高：基于此约束参数值的规一化可以帮助简化学习速率选择过程。

总结

1 Dropout存在两个版本：直接（不常用）和反转

2 单个神经元上的dropout可以使用伯努利随机变量建模

3 可以使用二项式随机变量来对一组神经元上的舍弃进行建模

4 即使舍弃神经元恰巧为np的概率是低的，但平均上np个神经元被舍弃。

5 Inverted Dropout提高学习率

6 Inverted Dropout应该与限制参数值的其他归一化技术一起使用，以便简化学习速率选择过程

7 Dropout有助于防止深层神经网络中的过度拟合

作者介绍：Paolo Galeone，计算机工程师以及深度学习研究者，专注于计算机视觉问题的研究

Blog：https://pgaleone.eu/

Linkedin：https://it.linkedin.com/in/paolo-galeone-6782b311b

Twitter：https://twitter.com/paolo_galeone