luogu1312 Mayan游戏 剪枝

题目大意

Mayan puzzle是最近流行起来的一个游戏。游戏界面是一个77 行\times 5×5列的棋盘，上面堆放着一些方块，方块不能悬空堆放，即方块必须放在最下面一行，或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块，消除方块的规则如下：

1 、每步移动可以且仅可以沿横向（即向左或向右）拖动某一方块一格：当拖动这一方块时，如果拖动后到达的位置（以下称目标位置）也有方块，那么这两个方块将交换位置（参见输入输出样例说明中的图66到图77 ）；如果目标位置上没有方块，那么被拖动的方块将从原来的竖列中抽出，并从目标位置上掉落（直到不悬空，参见下面图1 和图2）；

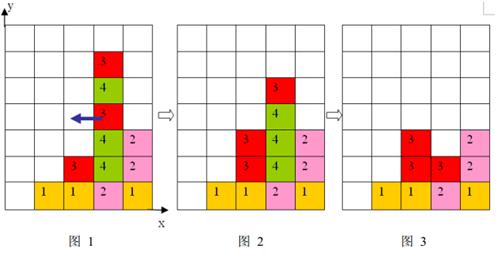
2 、任一时刻，如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除（参见图1 到图3）。

注意：

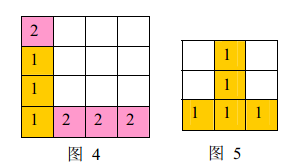
a) 如果同时有多组方块满足消除条件，几组方块会同时被消除（例如下面图44 ，三个颜色为11 的方块和三个颜色为 22 的方块会同时被消除，最后剩下一个颜色为22的方块）。

b) 当出现行和列都满足消除条件且行列共享某个方块时，行和列上满足消除条件的所有方块会被同时消除（例如下面图5 所示的情形，5 个方块会同时被消除）。

3 、方块消除之后，消除位置之上的方块将掉落，掉落后可能会引起新的方块消除。注意：掉落的过程中将不会有方块的消除。

上面图1 到图 3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为（0, 0 ），将位于（3, 3 ）的方块向左移动之后，游戏界面从图 1 变成图 2 所示的状态，此时在一竖列上有连续三块颜色为4 的方块，满足消除条件，消除连续3 块颜色为4 的方块后，上方的颜色为3 的方块掉落，形成图 3 所示的局面。

若有解，输出具体移动方案，否则输出-1.

题解

如何模拟消除过程

1. 每当我们消除掉一组块后，剩余的块新的排列方式我们是不可预估的。所以，我们应当不断对全局进行可消除的块的搜索并消除，而不是删除哪个块就在哪个块附近尝试考虑各种情况来删除。
2. 对于一组块如何删除？一定不要忘记图5的情况！另外，在时间复杂度够的情况下，我们要尽可能使用简单粗暴的形式解决问题。与其边删块边让上面的块下落，不如删的时候只删不下落，最后设置个DropAll函数把所有块整体下落，这样一定不会错。

如何剪枝

1. 优化搜索顺序：根据题目中的优先级，我们可以按从左到右、从下至上进行搜索。
2. 排除等效冗余：我们不允许两个颜色相同的块交换；所有块不可以与左侧相邻的块交换。
3. 可行性剪枝：本题看不出什么规律来，无法在此处剪枝。
4. 最优性剪枝：本题没要你求最优解，无法在此处剪枝。
5. 记忆化：本题状态存储不了，无法在此处剪枝。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cassert>
using namespace std;
 
const int MAX_ROW = 10, MAX_COL = 10;
const int TotX = 5, TotY = 7;
int N;
 
struct Matrix
{
	int A[MAX_ROW][MAX_COL];
 
private:
	int GetHorSum(int x, int y)
	{
		int color = A[x][y];
		int ans = 1;
		for (int i = x - 1; i >= 0 && A[i][y] == color; i--)
			ans++;
		for (int i = x + 1; i < TotX && A[i][y] == color; i++)
			ans++;
		return ans;
	}
 
	int GetVerSum(int x, int y)
	{
		int color = A[x][y];
		int ans = 1;
		for (int i = y + 1; i < TotY && A[x][i] == color; i++)
			ans++;
		for (int i = y - 1; i >= 0 && A[x][i] == color; i--)
			ans++;
		return ans;
	}
 
	void DropOne(int x, int y)
	{
		if (A[x][y])
			for (int i = y - 1; i >= 0 && !A[x][i]; i--)
				swap(A[x][i], A[x][i + 1]);
	}
 
	void DropAll()
	{
		for (int x = 0; x < TotX; x++)
			for (int y = 0; y < TotY; y++)
				DropOne(x, y);
	}
 
	void RemoveHor(int, int);
	void RemoveVer(int, int);
 
	bool Remove(int x, int y)
	{
		if (GetHorSum(x, y) >= 3)
		{
			RemoveHor(x, y);
			DropAll();
			return true;
		}
		if (GetVerSum(x, y) >= 3)
		{
			RemoveVer(x, y);
			DropAll();
			return true;
		}
		return false;
	}
 
	bool Search_Remove()
	{
		for (int x = 0; x < TotX; x++)
			for (int y = 0; y < TotY && A[x][y]; y++)
				if (Remove(x, y))
					return true;
		return false;
	}
 
	void RemoveAll()
	{
		while (Search_Remove());
	}
 
public:
	Matrix operator = (const Matrix& a)
	{
		memcpy(A, a.A, sizeof(a.A));
		return *this;
	}
 
	bool operator == (const Matrix& a) const
	{
		return !memcmp(A, a.A, sizeof(A));
	}
 
	bool Empty()
	{
		for (int x = 0; x < TotX; x++)
			if (A[x][0])
				return false;
		return true;
	}
 
	Matrix Move(int x, int y, int dir)
	{
		Matrix ans;
		ans = *this;
		assert(ans.A[x][y]);
		assert(x + dir < TotX && x + dir >= 0);
		if (ans.A[x + dir][y])
			swap(ans.A[x][y], ans.A[x + dir][y]);
		else
		{
			swap(ans.A[x][y], ans.A[x + dir][y]);
			ans.DropAll();
		}
		ans.RemoveAll();
		return ans;
	}
};
 
void Matrix::RemoveHor(int x, int y)
{
	int color = A[x][y];
	A[x][y] = 0;
	for (int i = x - 1; i >= 0 && A[i][y] == color; i--)
	{
		if (GetVerSum(i, y) >= 3)
			RemoveVer(i, y);
		A[i][y] = 0;
	}
	for (int i = x + 1; i < TotX && A[i][y] == color; i++)
	{
		if (GetVerSum(i, y) >= 3)
			RemoveVer(i, y);
		A[i][y] = 0;
	}
}
 
void Matrix::RemoveVer(int x, int y)
{
	int color = A[x][y];
	A[x][y] = 0;
	for (int i = y - 1; y >= 0 && A[x][i] == color; i--)
	{
		if (GetHorSum(x, i) >= 3)
			RemoveHor(x, i);
		A[x][i] = 0;
	}
	for (int i = y + 1; y < TotY && A[x][i] == color; i++)
	{
		if (GetHorSum(x, i) >= 3)
			RemoveHor(x, i);
		A[x][i] = 0;
	}
}
 
struct State
{
	Matrix mat;
	int X, Y, Dir;
}States[10];
 
bool Ok(int cnt)
{
	for (int i = 0; i < cnt; i++)
		if (States[i].mat == States[cnt].mat)
			return false;
	return true;
}
 
int Dfs(int cnt)
{
	if (cnt > N)
		return -1;
	for (int x = 0; x < TotX; x++)
		for (int y = 0; y < TotY && States[cnt - 1].mat.A[x][y]; y++)
		{
			States[cnt].X = x;
			States[cnt].Y = y;
			const Matrix& matFrom = States[cnt - 1].mat;
			if (x <= TotX - 2 && matFrom.A[x + 1][y] != matFrom.A[x][y])
			{
				States[cnt].Dir = 1;
				States[cnt].mat = States[cnt - 1].mat.Move(x, y, 1);
				if (States[cnt].mat.Empty())
					return cnt;
				if (Ok(cnt))
				{
					int nextAns = Dfs(cnt + 1);
					if (nextAns > -1)
						return nextAns;
				}
			}
			if (x >= 1 && !matFrom.A[x - 1][y])
			{
				States[cnt].Dir = -1;
				States[cnt].mat = States[cnt - 1].mat.Move(x, y, -1);
				if (States[cnt].mat.Empty())
					return cnt;
				if (Ok(cnt))
				{
					int nextAns = Dfs(cnt + 1);
					if (nextAns > -1)
						return nextAns;
				}
			}
		}
	return -1;
}
 
int main()
{
	scanf("%d", &N);
	for (int x = 0; x < TotX; x++)
		for (int y = 0; scanf("%d", &States[0].mat.A[x][y]) && States[0].mat.A[x][y]; y++);
 
	int cnt = Dfs(1);
	if (cnt == -1)
		printf("-1\n");
	else
	{
		for (int i = 1; i <= cnt; i++)
			printf("%d %d %d\n", States[i].X, States[i].Y, States[i].Dir);
	}
	return 0;
}