BZOJ 1016 最小生成树计数 【模板】最小生成树计数

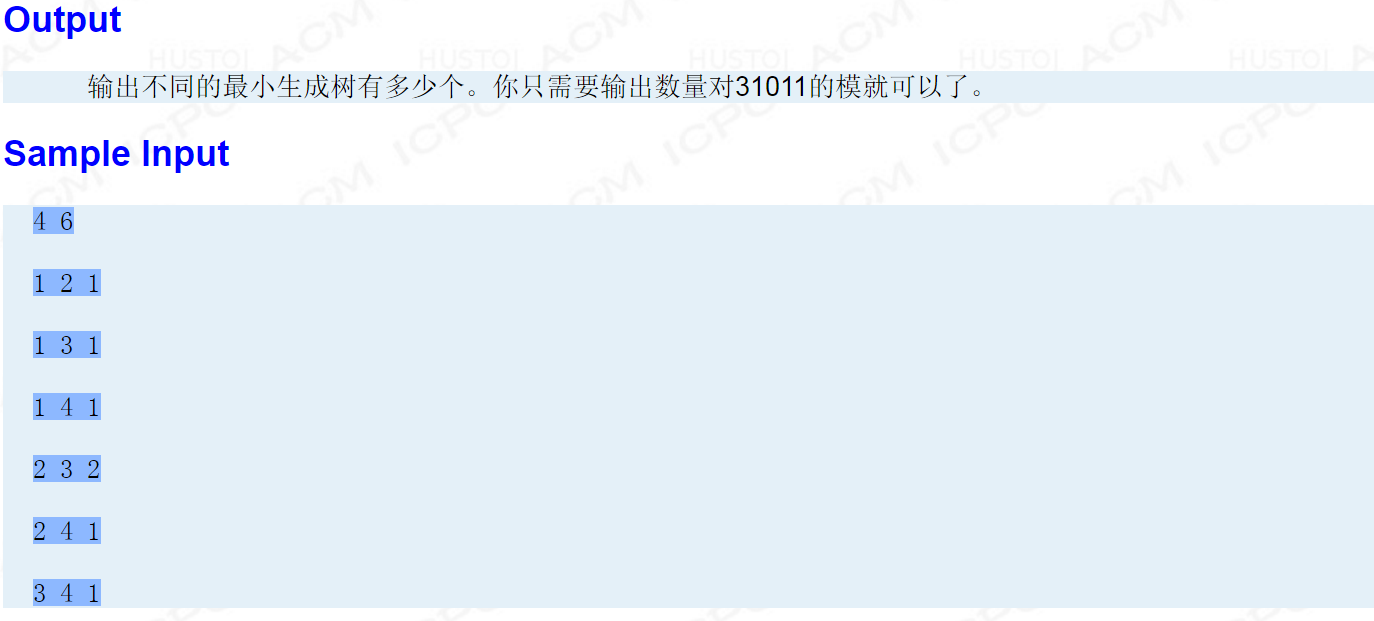
【题解】

对于不同的最小生成树，每种权值的边使用的数量是一定的，每种权值的边的作用是确定的

我们可以先做一遍Kruskal，求出每种权值的边的使用数量num

再对于每种权值的边，2^num搜索出合法使用方案，把每种权值的边的方案用乘法原理乘起来就是答案了

 #include<cstdio>
 #include<algorithm>
 using namespace std;
 const int maxn=,Mod=;
 int n,m,tot,sum,ans=,cnt,st[maxn],fa[maxn],num[maxn];
 struct edge{int x,y,dis,pos;}e[maxn];
 void read(int &k){
     k=; int f=; char c=getchar();
     while(c<''||c>'')c=='-'&&(f=-),c=getchar();
     while(''<=c&&c<='')k=k*+c-'',c=getchar();
     k*=f;
 }
 int find(int x){return fa[x]==x?x:find(fa[x]);}
 void dfs(int kind,int now,int chosen){
     if (now==st[kind+]){
         if (chosen==num[kind]) sum++;
         return;
     }
     int p=find(e[now].x),q=find(e[now].y);
     if (p!=q) fa[p]=q,dfs(kind,now+,chosen+),fa[p]=p,fa[q]=q;
     dfs(kind,now+,chosen);
 }
 bool cmp(edge a,edge b){return a.dis<b.dis;}
 int main(){
     read(n); read(m);
     for (int i=;i<=m;i++)read(e[i].x),read(e[i].y),read(e[i].dis);
     sort(e+,e+m+,cmp);
     for (int i=;i<=m;i++) {
         if (e[i].dis!=e[i-].dis) st[++cnt]=i;
         e[i].pos=cnt;
     }
     st[cnt+]=m+;
     for (int i=;i<=n;i++) fa[i]=i;
     for (int i=,x,y;i<=m;i++)
         if ((x=find(e[i].x))!=(y=find(e[i].y))) fa[x]=y,num[e[i].pos]++,tot++;
     if (tot!=n-) return puts(""),;
     for (int i=;i<=n;i++) fa[i]=i;
     for (int i=;i<=cnt;i++) if(num[i]){
         sum=; dfs(i,st[i],);
         for (int j=st[i];j<st[i+];j++) fa[find(e[j].x)]=find(e[j].y);
         ans=1LL*ans*sum%Mod;
     }
     printf("%d",ans);
     return ;
 }