Codeforces 985 最短水桶分配 沙堆构造 贪心单调对列

A

B

/* Huyyt */
#include <bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define mkp(a,b) make_pair(a,b)
#define pb push_back
const int dir[][] = {{, }, {, }, {, -}, { -, }, {, }, {, -}, { -, -}, { -, }};
using namespace std;
typedef long long ll;
inline void read(int &v)
{
        v = ;
        char c = ;
        int p = ;
        while (c < '' || c > '')
        {
                if (c == '-')
                {
                        p = -;
                }
                c = getchar();
        }
        while (c >= '' && c <= '')
        {
                v = (v << ) + (v << ) + c - '';
                c = getchar();
        }
        v *= p;
}
const long long mod = 1e9 + ;
const int N = 1e5 + ;
int n;
char f[][];
int num[];
int main()
{
        int n, m;
        cin >> n >> m;
        for (int i = ; i <= n; i++)
        {
                scanf("%s", f[i] + );
        }
        for (int i = ; i <= n; i++)
        {
                for (int j = ; j <= m; j++)
                {
                        if (f[i][j] == '')
                        {
                                num[j]++;
                        }
                }
        }
        int flag;
        for (int i = ; i <= n; i++)
        {
                flag = ;
                for (int j = ; j <= m; j++)
                {
                        if (f[i][j] == '' && num[j] == )
                        {
                                flag = ;
                                break;
                        }
                }
                if (flag)
                {
                        cout << "YES" << endl;
                        return ;
                }
        }
        cout << "NO" << endl;
        return ;
}

C

/* Huyyt */
#include <bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define mkp(a,b) make_pair(a,b)
#define pb push_back
const int dir[][] = {{, }, {, }, {, -}, { -, }, {, }, {, -}, { -, -}, { -, }};
using namespace std;
typedef long long ll;
inline void read(int &v)
{
        v = ;
        char c = ;
        int p = ;
        while (c < '' || c > '')
        {
                if (c == '-')
                {
                        p = -;
                }
                c = getchar();
        }
        while (c >= '' && c <= '')
        {
                v = (v << ) + (v << ) + c - '';
                c = getchar();
        }
        v *= p;
}
const long long mod = 1e9 + ;
const int N = 1e5 + ;
int n;
ll num[N];
priority_queue<ll, vector<ll>, less<ll> >que;
queue<ll> q;
int main()
{
        int n, k;
        ll l;
        ll minn = INT_MAX;
        ll anser = ;
        cin >> n >> k >> l;
        for (int i = ; i <= n * k; i++)
        {
                scanf("%d", &num[i]);
                minn = min(minn, num[i]);
        }
        int cnt = ;
        if (k == )
        {
                for (int i = ; i <= n * k; i++)
                {
                        if (num[i] > minn + l)
                        {
                                cout <<  << endl;
                                return ;
                        }
                        anser += num[i];
                }
                cout << anser << endl;
                return ;
        }
        //cout<<minn<<endl;
        for (int i = ; i <= n * k; i++)
        {
                if (num[i] <= minn + l)
                {
                        que.push(num[i]);
                }
                else
                {
                        q.push(num[i]);
                }
        }
        while (n--)
        {
                for (int i = ; i <= k - ; i++)
                {
                        if (que.empty())
                        {
                                cout <<  << endl;
                                return ;
                        }
                        if (q.empty())
                        {
                                if (que.size() > )
                                {
                                        //cout<<que.top()<<endl;
                                        que.pop();
                                }
                                else
                                {
                                        cout <<  << endl;
                                        return ;
                                }
                        }
                        else
                        {
                                //cout<<q.front()<<endl;
                                q.pop();
                        }
                }
                //cout<<que.top()<<endl;
                ll now = que.top();
                que.pop();
                //cout<<endl;
                if (now > minn + l)
                {
                        cout <<  << endl;
                        return ;
                }
                else
                {
                        anser += now;
                }
        }
        cout << anser << endl;
        return ;
}

D. Sand Fortress

给你N高度的沙子 要求你堆出刚好N高度的沙子 相邻的两个沙子差距不超过1 第一堆沙子不超过H

解:

①

官方题解:

先考虑金字塔型1到K到1 这样得到的总数为k*(k+1)/2-k=k²

然后我们贪心把剩下的n-k²都用k来放 再需要用的总数就是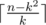

可以证明对于任意k从2到 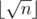 这个函数从1开始是递增的

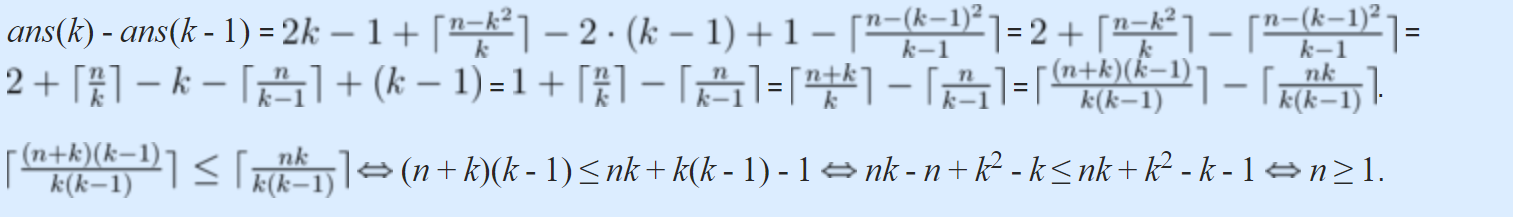
然后贪心地把金字塔尽量往左移 即让初始的h₁=min(k,H)

则左移后的沙子总数为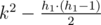 

所以我们需要做的是找到最大的k使得当h1=min(k,H)时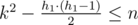 

当恰好为n时 不用补充 小于n时 用k去补充

#include <bits/stdc++.h>

#define forn(i, n) for (int i = 0; i < int(n); i++)

typedef long long li;

using namespace std;

const int INF = 2e9;
li n, h;

bool check(li maxh){
    li k = min(h, maxh);
    li cnt = maxh * maxh - k * (k - ) / ;
    return (cnt <= n);
}

li get(li maxh){
    li k = min(h, maxh);
    li cnt = maxh * maxh - k * (k - ) / ;
    li len = ( * maxh - ) - (k - );
    n -= cnt;
    return len + (n + maxh - ) / maxh;
}

int main() {
    scanf("%lld%lld", &n, &h);
    li l = , r = INF;

    while (l < r - ){
        li m = (l + r) / ;

        if (check(m))
            l = m;
        else
            r = m;
    }

    printf("%lld\n", check(r) ? get(r) : get(l));
    return ;
}

②(和官方差不多)

构造两种

第一种为三角形 第二种为梯形

两种分别二分构造 然后取最小值即可

E. Pencils and Boxes

给你一个N个数字的数组,要求你把每个数字都放入一个盒子

每个数字只属于一个盒子 每个盒子至少要有K个数字 每个盒子的极差不超过d

能实现的话YES 否则NO

解:

贪心 单调队列

先排序 然后贪心 很容易想到一个盒子里能放多少连续的就尽量放多少

通过单调队列实现能放多少尽量放多少的操作

/* Huyyt */
#include <bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define mkp(a,b) make_pair(a,b)
#define pb push_back
const int dir[][] = {{, }, {, }, {, -}, { -, }, {, }, {, -}, { -, -}, { -, }};
using namespace std;
typedef long long ll;
inline void read(int &v)
{
        v = ;
        char c = ;
        int p = ;
        while (c < '' || c > '')
        {
                if (c == '-')
                {
                        p = -;
                }
                c = getchar();
        }
        while (c >= '' && c <= '')
        {
                v = (v << ) + (v << ) + c - '';
                c = getchar();
        }
        v *= p;
}
const long long mod = 1e9 + ;
const int N = 5e5 + ;
int n;
int num[N];
int q[N];
int main()
{
        int k, d;
        read(n), read(k), read(d);
        for (int i = ; i <= n; i++)
        {
                read(num[i]);
        }
        int now;
        sort(num + , num +  + n);
        int head = ;
        int tail = ;
        for (int i = k; i <= n; i++)
        {
                while (head <= tail && num[i] - num[q[head] + ] > d)
                {
                        head++;
                }
                if (head <= tail && i - q[head] >= k)
                {
                        q[++tail] = i;
                }
        }
        if (q[tail] == n)
        {
                cout << "YES" << endl;
        }
        else
        {
                cout << "NO" << endl;
        }
        return ;
}

F