UOJ#339. 【清华集训2017】小 Y 和二叉树 贪心

原文链接 www.cnblogs.com/zhouzhendong/p/UOJ339.html

前言

好久没更博客了，前来更一发。

题解

首先，我们考虑一个子问题：给定根，求出最小中序遍历。

如果根节点有一个儿子，那么，我们需要比较根节点和 儿子的最小中序遍历的第一个元素，选择较优的一方放在前面。

如果根节点有两个儿子，那么，我们必然选择最小中序遍历较小的儿子放在左儿子。

由于所有节点编号互不相同，所以我们在比较两个部分的字典序时，只关注第一个元素的大小。

可以发现，一个有两个儿子的节点是不可能作为以它为根的子树的最小字典序的第一个元素的，接着，我们发现，除了这些节点之外的节点都可以作为最小字典序的第一个元素，构造方法如图所示：

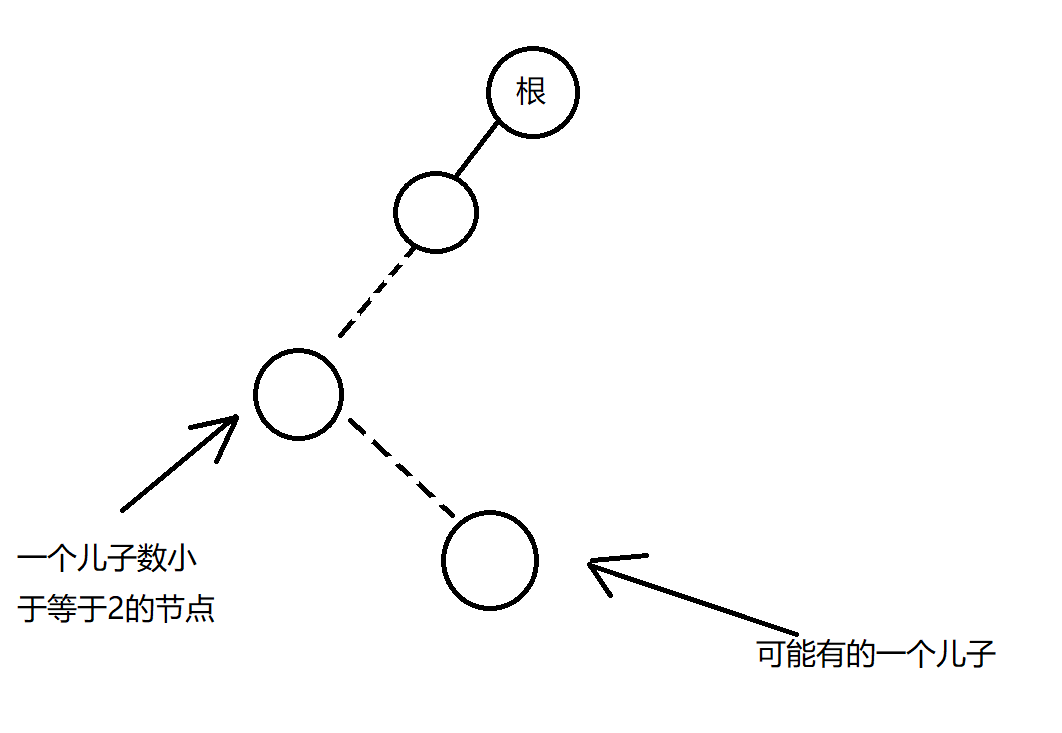
所以我们将子树中这类节点编号的最小值较小的节点作为左子树即可。

然后我们考虑不定根的情况。

首先，我们关注最小字典序的第一元素，它一定是度数小于3的最小编号节点。我们以这个节点为根处理出每一个子树的最小字典序的第一个元素，并将左右儿子中字典序较小的一方放在左儿子。

我们将这个节点设为 x 。

如果 x 的度数为 2，那么，选择字典序较小的子树作为它的右子树，将其另一个子树的根的左儿子（对于这棵子树，我们就用之前提到的有根树的方式来解决），然后切除这条边，让这个子树的根取代 x ，并继续重复执行类似操作。

如果 x 的度数为 1，设 x 的儿子为 y。

如果 y 有儿子，那么，y、y 的左子树的最小字典序的第一个元素 都可能作为下一个元素，所以我们要取较优的一方：假设让 y 作为下一个元素，那么令最终构造方案中 y 的左儿子为 x，然后切除 x 与 y 之间的边，让 y 取代 x，并重复执行类似操作；如果选择 y 的左子树，那么就令 y 作为 x 的右儿子，并直接套用之前提到的有根树的解决方法来处理子树 y。

如果 y 只有一个儿子，那么，将 y 作为 x 的右儿子或者将 x 作为 y 的左儿子的效果完全相同，但是将 x 作为 y 的左儿子可以保留让 y 的儿子 z 作为 z 子树的中序遍历的最小元素的机会，所以我们选择将 x 作为 y 的左儿子。

P.S. 我觉得看题解说分讨不如直接看代码。。。。

代码

#include <bits/stdc++.h>
#define clr(x) memset(x,0,sizeof (x))
#define For(i,a,b) for (int i=a;i<=b;i++)
#define Fod(i,b,a) for (int i=b;i>=a;i--)
#define pb(x) push_back(x)
#define mp(x,y) make_pair(x,y)
#define fi first
#define se second
#define _SEED_ ('C'+'L'+'Y'+'A'+'K'+'I'+'O'+'I')
#define outval(x) printf(#x" = %d\n",x)
#define outvec(x) printf("vec "#x" = ");for (auto _v : x)printf("%d ",_v);puts("")
#define outtag(x) puts("----------"#x"----------")
#define outarr(a,L,R) printf(#a"[%d...%d] = ",L,R);\
						For(_v2,L,R)printf("%d ",a[_v2]);puts("");
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef vector <int> vi;
LL read(){
	LL x=0,f=0;
	char ch=getchar();
	while (!isdigit(ch))
		f|=ch=='-',ch=getchar();
	while (isdigit(ch))
		x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return f?-x:x;
}
const int N=1e6+5;
int n;
vector <int> e[N];
int mi[N];
int son[N][2];
void dfs(int x,int pre){
	mi[x]=e[x].size()!=3?x:n+1;
	for (auto y : e[x])
		if (y!=pre){
			dfs(y,x);
			mi[x]=min(mi[x],mi[y]);
			son[x][son[x][0]!=0]=y;
		}
	if (mi[son[x][0]]>mi[son[x][1]])
		swap(son[x][0],son[x][1]);
}
vector <int> ans;
void calc(int x){
	if (!x)
		return;
	if (son[x][0]&&son[x][1])
		calc(son[x][0]),ans.pb(x),calc(son[x][1]);
	else if (x<mi[son[x][0]])
		ans.pb(x),calc(son[x][0]);
	else
		calc(son[x][0]),ans.pb(x);
}
void solve(int x){
	ans.pb(x);
	if (!son[x][0])
		return;
	if (son[x][1])
		calc(son[x][0]),solve(son[x][1]);
	else {
		x=son[x][0];
		if (x<=mi[x])
			solve(x);
		else
			calc(x);
	}
}
int main(){
	n=read();
	For(i,1,n){
		int k=read();
		while (k--)
			e[i].pb(read());
	}
	int x=mi[0]=n+1;
	For(i,1,n)
		if (e[i].size()!=3)
			x=min(x,i);
	dfs(x,0);
	solve(x);
	for (auto i : ans)
		printf("%d ",i);
	return 0;
}