Kotlin扩展作用域分析与扩展的根本作用解析

在上一次https://www.cnblogs.com/webor2006/p/11219358.html学习了Kotlin的扩展，继续这个话题继续拓展，首先提出这么一个问题：假如我们扩展的方法跟类中已有的方法一模一样，那最终调用的哪个方法呢？虽说这个问题有点白痴，但是为了学习得更加透彻有必要对这些细节也了解透，下面来试验一下：

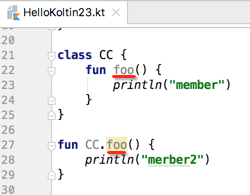
调用看一下：

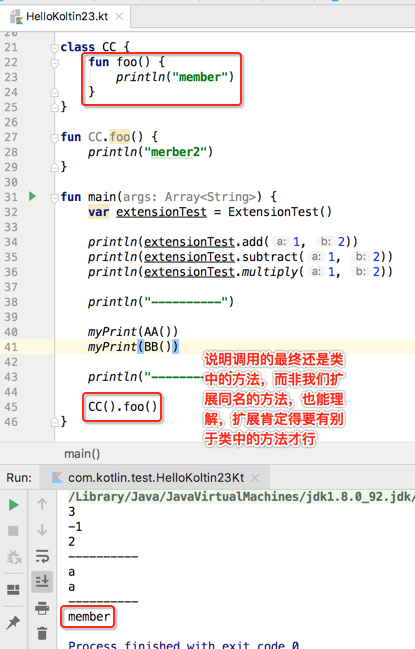
另外扩展方法也可以对已有方法进行重载，如下：

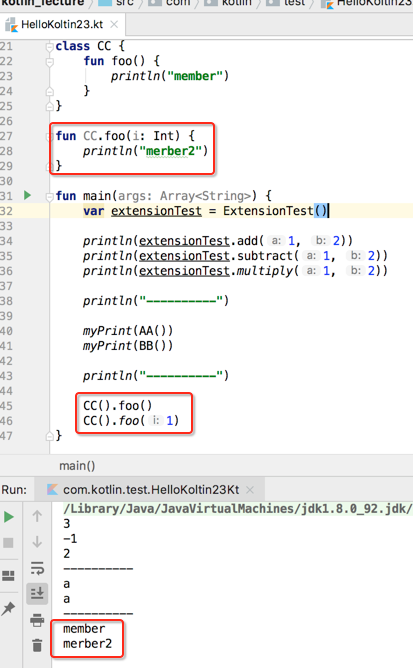
可空类型的扩展：

啥意思？我们知道Any是Kotlin所有类的顶层父类，所以我们可以对这个顶层类进行扩展，如下：

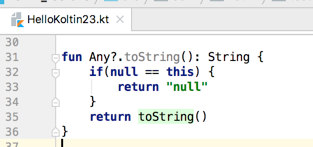
有啥意义？由于已经做了null的判断了，也就是如果扩展了Any为空的toString()的话，那就避免了我们在实际中的空指针异常了，利用扩展特性可以很好的进行规避。

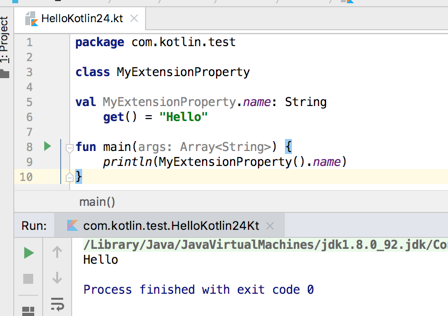
扩展属性：

除了扩展函数之外，还可以扩展属性，比较简单，直接看个代码既可：

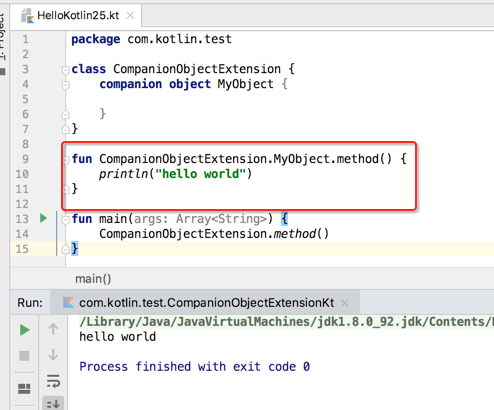
伴生对象的扩展：

也比较简单，直接上程序：

扩展的作用域分析：

对于扩展来说，其实也会有作用域的概念，下面先抛出理论：

1、扩展函数所定义在的类实例叫做分发接收者（dispatch receiver）。

2、扩展函数所扩展的那个类的实例叫做扩展接收者（extension receiver）。

3、当以上两个名字出现冲突时，扩展接收者的优先级最高。

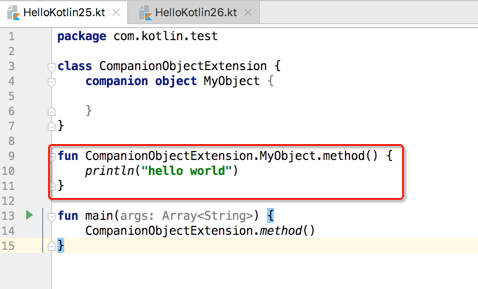
是不是一头雾水，不要紧，接下来咱们举例来说明，之前我们的扩展定义都是在顶层的，如下：

其实它可以在类中进行定义，如下：

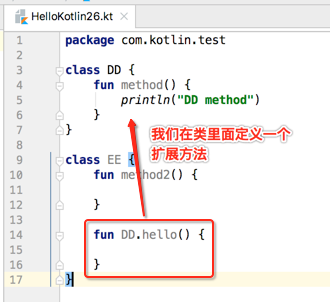
其中该方法是对DD类的扩展，所以它就可以DD已经拥有的成员，比如：

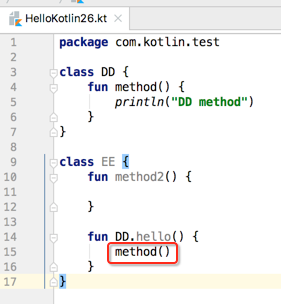
除此之外，还能够使用定义这个扩展方法所在类的成员，也就是发接收者（dispatch receiver）的成员，指的是：

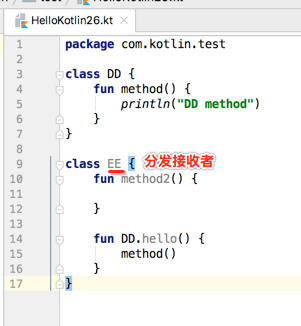
如下：

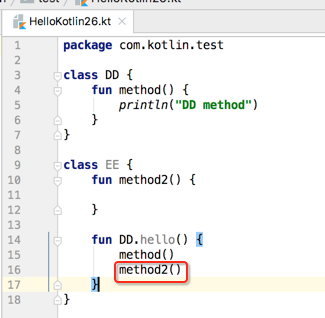
接下来再来定义一个方法：

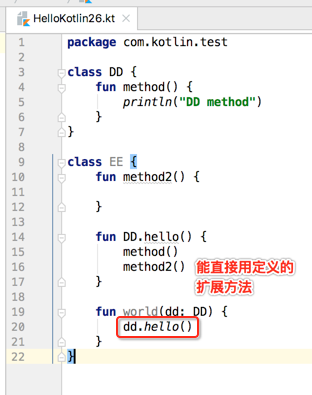
接下来再来扩展一个方法：

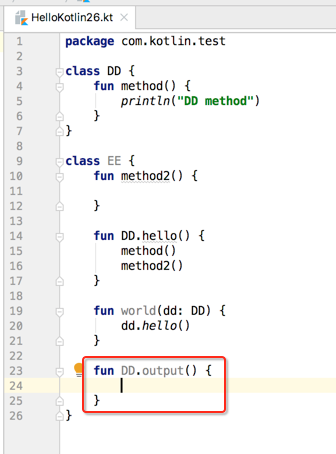
接下来看一下神操作：

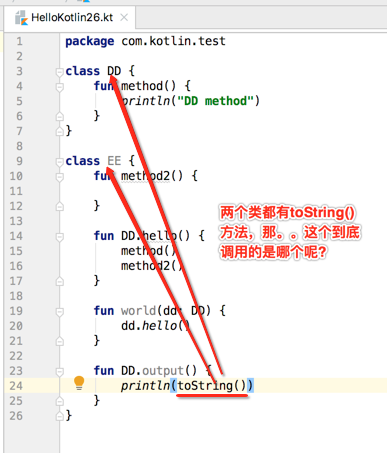
接一来看之前的这个理论：“3、当以上两个名字出现冲突时，扩展接收者的优先级最高。”，这条规则就已经说明了答案，啥是扩展接收者呀，看定义：“2、扩展函数所扩展的那个类的实例叫做扩展接收者（extension receiver）。”，所以指的是：

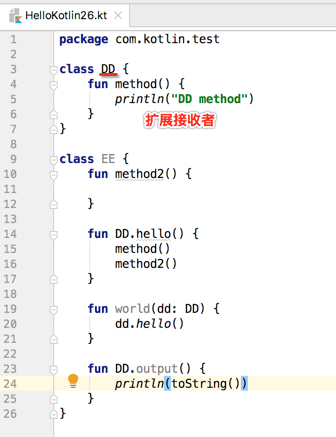
所以，这个输出肯定是输出的DD.toString()，那。。假如我想还要打印EE.toString()呢，Kotlin也提供有机制，如下：

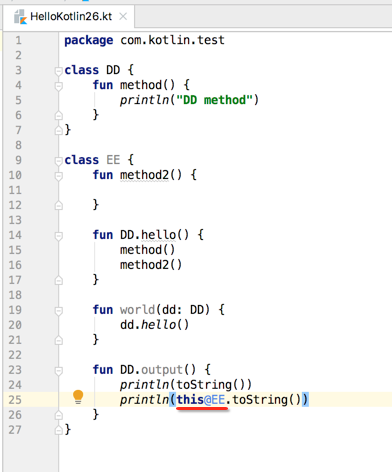
接下来再来定义一个方法：

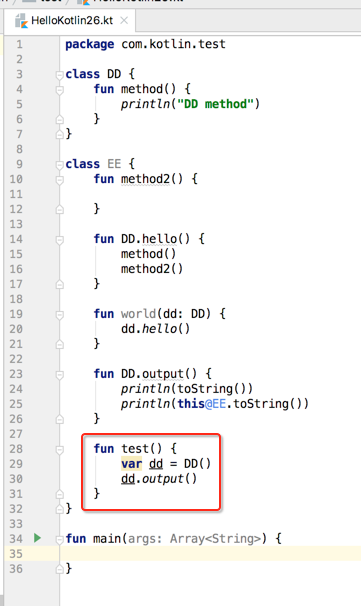
写这个方法是为了衬托扩展的作用域的，下面咱们在main方法中也来调用DD.output()，你会发现奇迹：

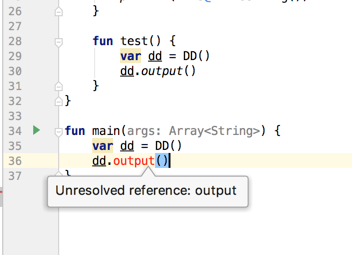
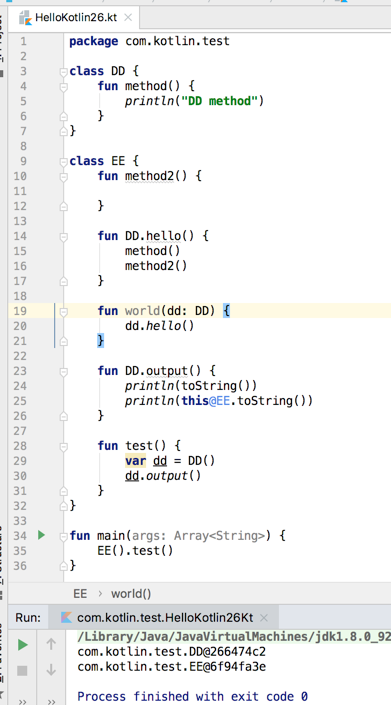
居然找不到这个扩展的方法，为啥？因为output的扩展是在EE里面声明的，所以它的扩展只能在EE里面使用，这也道出了扩展的作用域了，好，接下来调用test()方法：

扩展的根本作用：

好，接下来对扩展进行一个总结，扩展到底有啥用呢？其实它可以很好地解决Java中充斥的各种辅助类问题，怎么理解，我们可以回顾一下在Collections.java中充斥了大量的辅助类，比如：

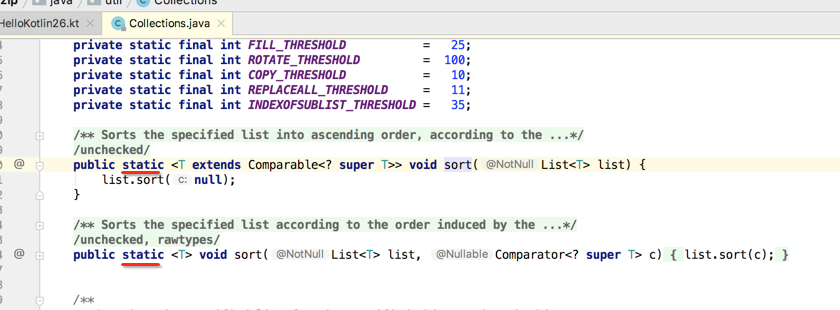
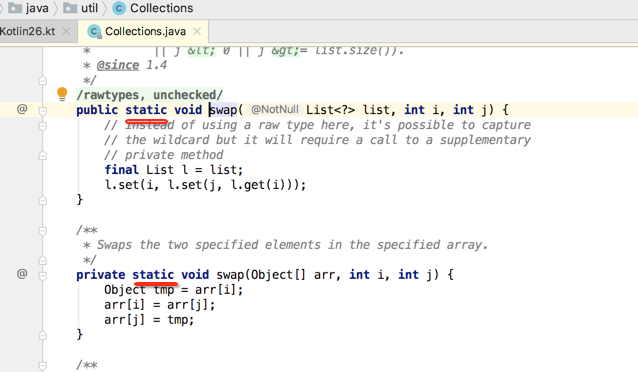
像这些排序照理应该就是本身属于集合中的，不应该还得用一个辅助类来搞，那通过Kotlin的扩展功能就可以很轻松的简化原来Java辅助类的功能呢？比如swap()方法，原来用java的方式写法是这样的：

而用了Kotlin的扩展功能可以简化为：

也就是系统集合木有提供swap方法，但是可以用Kotlin的扩展功能给集合加上该功能，再比如binarySearch()，原来得这样写：

而用了Kotlin的扩展会简化为：