Trie字典树（超详细！！！）

介绍

字典树，也称Trie、字母树，指的是某个字符串集合对应的形如下图的有根树。树的每条边上对应有恰好一个字符，每个顶点代表从根到该节点的路径所对应的字符串（将所有经过的边上的字符按顺序连接起来）。有时我们也称Trie上的边为转移，顶点为状态。

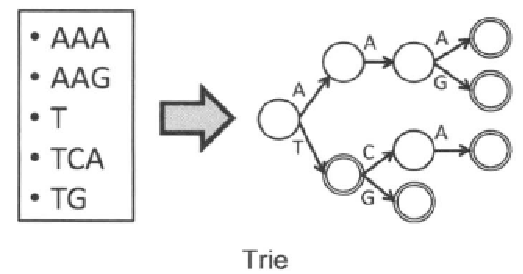
流程

初始化

一棵空Trie仅包含一个根节点，该点的字符指针均指向空。

插入

当需要插入一个字符串S时，我们令一个指针P起初指向根节点。然后，依次扫描S中的每个字符 c :

1．若P的c字符指针指向一个己经存在的节点Q，则令P＝Q。

2．若P的c字符指针指向空，则新建一个节点Q ，令P的 c 字符指针指向Q，然后令P＝Q。 当S中的字符扫描完毕时，在当前节点P上标记它是一个字符串的末尾。

查询

当需要查询一个字符串S在Trie中是否存在时，我们令一个指针P起初指向根节点，然后依次扫描S中的每个字符c :

1．若P的c字符指针指向空，则说明S没有被插入过Trie ，结束查询。

2．若P的c字符指针指向一个已经存在的节点Q，则令P=Q 。

当S中的字符扫描完毕时，若当前节点P被标记为一个字符串的末尾，则说明S 在 Trie 中存在，否则说明S没有被插入过Trie。

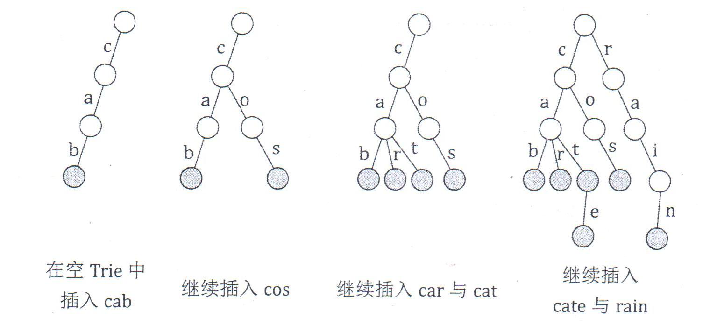
在上图所示的例子中，需要插入和查询的字符串都由小写字母构成，所以Trie 的每个节点具有 26个字符指针，分别为a到z。上图展示了在一棵空 Trie中依次插入 " cab " " cos " " car " " cat " " cate"和"rain"后的Trie 的形态，灰色标记了单词的末尾节点。

可以看出在Trie 中，字符数据都体现在树的边(指针)上，树的节点仅保存一些额外信息，例如单词结尾标记等。其空间复杂度是O ( NC ) ，其中 N 是节点个数， C是字符集的大小。

初始化
.int ch[N][Z];   //Z为字符集大小  
.bool bo[N];   
 //若bo=true则表示从根到该点经过的边上字母组成的字符串是实际字符串集合中的元素

现在要对一个字符集为小写英文字母的Trie插入一个字符串S：
.void insert(char *s) {               //char *s表示一个字符数组  
.    int len = strlen(s);  
.    int u = ;                       //1为根节点 
.    for(int i = ; i < len; ++i){  
.        int c = s[i] - 'a';  
.        if(!ch[u][c])  
.        ch[u][c] = ++tot;  //若不存在这条边则要新建一个节点与转移边
.        u = ch[u][c];      //tot为总点数 
.      }  
.   bo[u] = true; 
.  //在串的结尾处将bo赋值，表示它代表一个实际字符串集合中的元素
.}

查询一个字符串S是否是给定字符串集合中某个串的前缀：
.bool find(char s[]) {  
.    int len = strlen(s);  
.    int u = ;  
.    for(int i = ; i < len; ++i){  
.        int c = s[i] - 'a';  
.        if(!ch[u][c]) return false;  
.        u = ch[u][c];  
.    }  
.    return true;  
.}  

---

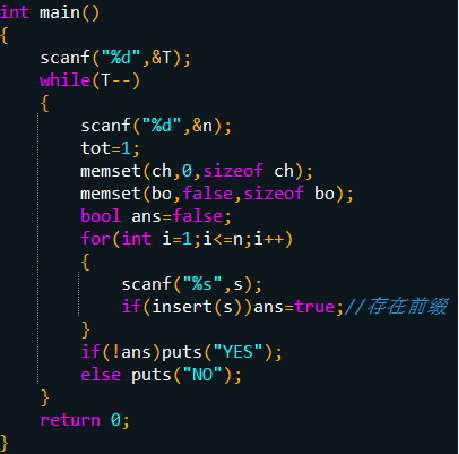
【例题1】Phone List（信息学奥赛一本通 1471）

【题目描述】

给定 n 个长度不超过 10 的数字串，问其中是否存在两个数字串 S,T，使得 S 是 T 的前缀，多组数据。

【输入】

第一行一个整数 T，表示数据组数。 对于每组数据，第一行一个数 n，接下来 n 行输入 n 个数字串。

【输出】

对于每组数据，若存在两个数字串 S，T，使得 S 是 T 的前缀，则输出 NO ，否则输出 YES 。 请注意此处结果与输出的对应关系！

【输入样例】

2

3

911

97625999

91125426

5

113

12340

123440

12345

98346

【输出样例】

NO

YES

---

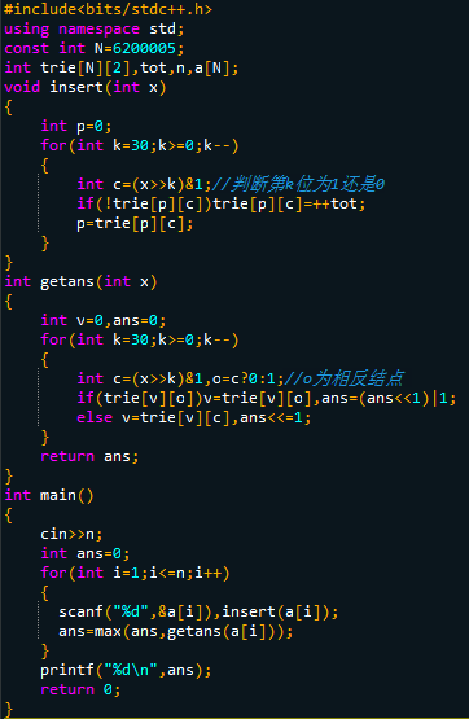
【例题2】The XOR Largest Pair（信息学奥赛一本通 1472）

【题目描述】

在给定的 N 个整数 A1,A2,…, AN 中选出两个进行异或运算，得到的结果最大是多少？

【输入】

第一行一个整数 N。 第二行 N 个整数 Ai。

【输出】

一个整数表示答案。

【输入样例】

5

2 9 5 7 0

【输出样例】

14

思路：

对于每个 i ( 1<=i <= N ) ，我们希望找到一个 j ( 1 <=j < i ) ，使Ai xor Aj最大。

我们可以把每个整数看作长度为 32 的二进制 01 串(数值较小时在前边补 0 )，并且把A1~Ai-1对应的 32 位二进制串插入一棵 Trie 树(最低二进制位为叶子节点)。接下来，对于 Ai 对应的 32 位二进制串，我们在 Trie 中进行一次与查询类似的过程，每一步都尝试沿着“与 Ai 的当前位相反的字符指针”向下访问。若“与 Ai 的当前位相反的字符指针”指向空节点，则只好访问与 Ai 当前位相同的字符指针。根据 xor 运算“相同得 0 ，不同得 1 ”的性质，该方法即可找出与 A i做 xor 运算结果最大的Aj。