机器学习---用python实现感知机算法和口袋算法（Machine Learning PLA Pocket Algorithm Application）

之前在《机器学习---感知机（Machine Learning Perceptron）》一文中介绍了感知机算法的理论知识，现在让我们来实践一下。

有两个数据文件：data1和data2，分别用于PLA和Pocket Algorithm。可在以下地址下载：https://github.com/RedstoneWill/MachineLearningInAction/tree/master/Perceptron%20Linear%20Algorithm/data。

先回顾一下感知机算法：

1，初始化w

2，找出一个分类错误点

3，修正错误，假设迭代次数为t次（t=1,2,...），那么修正公式为：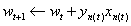

4，直至没有分类错误点，返回最终的w

接下来让我们按照算法步骤，一步一步进行。

首先导入需要用到的库，其中pandas用于读取数据文件，matplotlib用于画图，numpy用于数组运算：

import pandas as pd
import matplotlib.pyplot as plt
fig,ax=plt.subplots()
import numpy as np

读取数据文件：

data=pd.read_csv(r"...\data1.csv",header=None)

提取特征和目标：

X=data.iloc[:,[0,1]]  #提取特征
y=data[2]   #提取目标

提取不同类别的数据，用于画图：

x_positive=X[y==1]
x_negative=X[y==-1]

画图：

ax.scatter(x_positive[0],x_positive[1],marker="o",label="y=+1")
ax.scatter(x_negative[0],x_negative[1],marker="x",label="y=-1")
ax.legend()
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_title("Original Data")

从上图可以看到数据是线性可分的，接下来我们先把数据归一化：

mean=X.mean(axis=0)
sigma=X.std(axis=0)
X=(X-mean)/sigma

再画图看看：

设置好特征和权重，用于数组运算：

X[2]=np.ones((X.shape[0],1))   #给特征增加一列常数项
X=X.values    #把特征转换成ndarray格式

###初始化w###
w=X[0].copy()  #选取原点到第一个点的向量作为w的初始值
w[2]=0  #增加一项---阈值，阈值初始化为0
w=w.reshape(3,1)

画出初始法向量和初始分类直线（因为是在二维空间，所以是直线）：

###画出初始法向量###
ax.scatter(w[0],w[1],color="red")
ax.plot([0,w[0]],[0,w[1]])  

###画出初始分类直线###
line_x=np.linspace(-3,3,10)
line_y=(-w[2]-w[0]*line_x)/w[1]
ax.plot(line_x,line_y)

注：因为w₁x₁+w₂x₂+b=0，现在我们已经有了w和b的值，因此只需要设置x₁的值，就可以计算出x₂的值。

注：注意要适当调整一下图像比例，否则显示出来不对，具体请见完整代码。

现在我们已经完成初始化w的工作，接下去就是要找出分类错误点。现在的思路是：先计算出在当前参数w下的预测目标，然后把其和目标y进行比较，这样就可以知道分类错误的地方了。

scores=np.dot(X,w)  #把特征和权重点乘，得到目前参数下预测出的目标分数

y_pred=np.ones((scores.shape[0],1))  #设置预测目标，初始化值全为1，形状和目标分数相同
y=y.values.reshape((y_pred.shape[0],1))  #把目标转换成ndarray格式，形状和预测目标相同

loc_negative=np.where(scores<0)[0]  #标记分数为负数的地方
y_pred[loc_negative]=-1  #使标记为负数的地方预测目标变为-1

loc_wrong=np.where(y_pred!=y)[0]  #标记分类错误的地方

找出分类错误点后，我们对w进行修正（这里选取第一个分类错误点进行更新）：

w=w+y[loc_wrong][0]*X[loc_wrong,:][0].reshape(3,1)

最后进行迭代就可以找出最终的w：

for i in range(100):
    scores=np.dot(X,w)  #把特征和权重点乘，得到此参数下预测出的目标分数

    y_pred=np.ones((scores.shape[0],1))  #设置预测目标，初始化值全为1，形状和目标分数相同

    loc_negative=np.where(scores<0)[0]  #标记分数为负数的地方
    y_pred[loc_negative]=-1  #使标记为负数的地方预测目标变为-1

    loc_wrong=np.where(y_pred!=y)[0]  #标记分类错误的地方
    print("错误分类点有{}个。".format(len(loc_wrong)))
    if len(loc_wrong)>0:
        w=w+y[loc_wrong][0]*X[loc_wrong,:][0].reshape(3,1)
    else:
        break

print("参数w:{}".format(w))
print("分类直线:{}x1+{}x2+{}=0".format(w[0][0],w[1][0],w[2][0]))
line_x=np.linspace(-3,3,10)
line_y=(-w[2]-w[0]*line_x)/w[1]
ax.plot(line_x,line_y)

运行结果：

错误分类点有5个。
错误分类点有2个。
错误分类点有3个。
错误分类点有0个。
参数w:[[0.24622161]
 [2.81328976]
 [1.        ]]
分类直线:0.2462216100520832x1+2.8132897563595076x2+1.0=0

画出的分类直线：

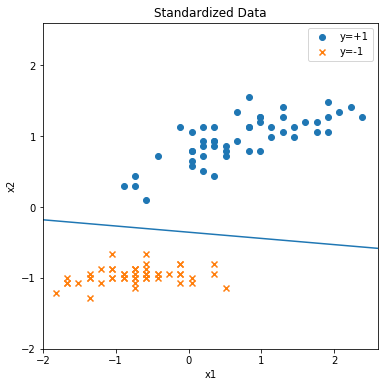
最后的最后，将上述代码整理一下。感知机算法完整代码如下（除去用于画图的代码，核心代码不到20行）：

import pandas as pd
import matplotlib.pyplot as plt
fig,ax=plt.subplots(figsize=(6,6))
import numpy as np

data=pd.read_csv(r"...\data1.csv",header=None)

X=data.iloc[:,[0,1]]  #提取特征
y=data[2]   #提取目标

###把数据归一化###
mean=X.mean(axis=0)
sigma=X.std(axis=0)
X=(X-mean)/sigma

###提取不同类别的数据，用于画图###
x_positive=X[y==1]
x_negative=X[y==-1]

ax.scatter(x_positive[0],x_positive[1],marker="o",label="y=+1")
ax.scatter(x_negative[0],x_negative[1],marker="x",label="y=-1")
ax.legend()
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_title("Standardized Data")
ax.set_xlim(-2,2.6)
ax.set_ylim(-2,2.6)

X[2]=np.ones((X.shape[0],1))   #给特征增加一列常数项
X=X.values    #把特征转换成ndarray格式

###初始化w###
w=X[0].copy()  #选取原点到第一个点的向量作为w的初始值
w[2]=0  #增加一项---阈值，阈值初始化为0
w=w.reshape(3,1)

y=y.values.reshape(100,1)  #把目标转换成ndarray格式，形状和预测目标相同

def compare(X,w,y):
    ###用于比较预测目标y_pred和实际目标y是否相符，返回分类错误的地方loc_wrong###
    ###输入特征，权重，目标###
    scores=np.dot(X,w)  #把特征和权重点乘，得到此参数下预测出的目标分数

    y_pred=np.ones((scores.shape[0],1))  #设置预测目标，初始化值全为1，形状和目标分数相同

    loc_negative=np.where(scores<0)[0]  #标记分数为负数的地方
    y_pred[loc_negative]=-1  #使标记为负数的地方预测目标变为-1

    loc_wrong=np.where(y_pred!=y)[0]  #标记分类错误的地方

    return loc_wrong

def update(X,w,y):
    ###用于更新权重w，返回更新后的权重w###
    ###输入特征，权重，目标###
    w=w+y[compare(X,w,y)][0]*X[compare(X,w,y),:][0].reshape(3,1)
    return w

def perceptron(X,w,y):
    ###感知机算法，显示最终的权重和分类直线，并画出分类直线###
    ###输入特征，初始权重，目标###
    while len(compare(X,w,y))>0:
        print("错误分类点有{}个。".format(len(compare(X,w,y))))
        w=update(X,w,y)

    print("参数w:{}".format(w))
    print("分类直线:{}x1+{}x2+{}=0".format(w[0][0],w[1][0],w[2][0]))
    line_x=np.linspace(-3,3,10)
    line_y=(-w[2]-w[0]*line_x)/w[1]
    ax.plot(line_x,line_y)

plt.show()

---

接下来看一下data2文件和口袋算法的应用。首先回顾一下Pocket Algorithm：

1，初始化w，把w作为最好的解放入口袋

2，随机找出一个分类错误点

3，修正错误，假设迭代次数为t次（t=1,2,...），那么修正公式为：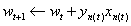

4，如果w_t+1比w犯的错误少，那么用w_t+1替代w，放入口袋

5，经过t次迭代后停止，返回口袋里最终的结果

口袋算法和PLA差不多，因此代码还是用上述感知机算法的框架，只需要局部修改一下即可。

首先画出原始数据图像和归一化后的数据图像：（代码和之前类似，故在此不再赘述）

     

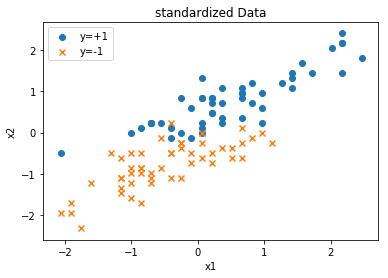
可以看到数据是线性不可分的。接下来修改一下perceptron函数和update函数。

def perceptron_pocket(X,w,y):
    ###感知机口袋算法，显示n次迭代后最好的权重和分类直线，并画出分类直线###
    ###输入特征，初始权重，目标###
    best_len=len(compare(X,w,y))  #初始化最少的分类错误点个数
    best_w=w  #初始化口袋里最好的参数w
    for i in range(100):
        print("错误分类点有{}个。".format(len(compare(X,w,y))))
        w=update(X,w,y)
        #如果当前参数下分类错误点个数小于最少的分类错误点个数，那么更新最少的分类错误点个数和口袋里最好的参数w
        if len(compare(X,w,y))<best_len:
            best_len=len(compare(X,w,y))
            best_w=w

    print("参数best_w:{}".format(best_w))
    print("分类直线:{}x1+{}x2+{}=0".format(best_w[0][0],best_w[1][0],best_w[2][0]))
    print("最少分类错误点的个数:{}个".format(best_len))
    line_x=np.linspace(-3,3,10)
    line_y=(-best_w[2]-best_w[0]*line_x)/best_w[1]
    ax.plot(line_x,line_y)

perceptron函数主要增加了一个口袋，用于存放最好的解，函数名称改为perceptron_pocket。

def update(X,w,y):
    ###用于更新权重w，返回更新后的权重w###
    ###输入特征，权重，目标###
    num=len(compare(X,w,y)) #分类错误点的个数
    w=w+y[compare(X,w,y)][np.random.choice(num)]*X[compare(X,w,y),:][np.random.choice(num)].reshape(3,1)
    return w

update函数将“选取第一个分类错误点进行更新”修改为“随机选取分类错误点进行更新”。

运行结果如下（由于带有随机性，每次运行结果都不同）：

错误分类点有9个。
错误分类点有30个。
错误分类点有11个。
错误分类点有24个。
错误分类点有5个。
错误分类点有22个。
错误分类点有16个。
错误分类点有17个。
错误分类点有5个。
错误分类点有15个。
错误分类点有5个。
错误分类点有15个。
错误分类点有6个。
错误分类点有13个。
错误分类点有7个。
错误分类点有12个。
错误分类点有9个。
错误分类点有14个。
错误分类点有12个。
错误分类点有16个。
错误分类点有9个。
错误分类点有10个。
错误分类点有12个。
错误分类点有12个。
错误分类点有7个。
错误分类点有16个。
错误分类点有5个。
错误分类点有7个。
错误分类点有6个。
错误分类点有10个。
错误分类点有6个。
错误分类点有9个。
错误分类点有11个。
错误分类点有7个。
错误分类点有5个。
错误分类点有11个。
错误分类点有6个。
错误分类点有8个。
错误分类点有6个。
错误分类点有12个。
错误分类点有6个。
错误分类点有11个。
错误分类点有14个。
错误分类点有10个。
错误分类点有5个。
错误分类点有5个。
错误分类点有5个。
错误分类点有4个。
错误分类点有6个。
错误分类点有6个。
错误分类点有6个。
错误分类点有9个。
错误分类点有6个。
错误分类点有10个。
错误分类点有6个。
错误分类点有7个。
错误分类点有6个。
错误分类点有10个。
错误分类点有6个。
错误分类点有10个。
错误分类点有5个。
错误分类点有10个。
错误分类点有6个。
错误分类点有8个。
错误分类点有6个。
错误分类点有5个。
错误分类点有6个。
错误分类点有7个。
错误分类点有9个。
错误分类点有7个。
错误分类点有6个。
错误分类点有7个。
错误分类点有6个。
错误分类点有4个。
错误分类点有6个。
错误分类点有10个。
错误分类点有6个。
错误分类点有11个。
错误分类点有15个。
错误分类点有10个。
错误分类点有5个。
错误分类点有5个。
错误分类点有6个。
错误分类点有9个。
错误分类点有6个。
错误分类点有8个。
错误分类点有5个。
错误分类点有10个。
错误分类点有5个。
错误分类点有10个。
错误分类点有6个。
错误分类点有10个。
错误分类点有18个。
错误分类点有9个。
错误分类点有10个。
错误分类点有10个。
错误分类点有5个。
错误分类点有5个。
错误分类点有6个。
错误分类点有8个。
参数best_w:[[-1.09227879]
 [ 5.19393394]
 [ 1.        ]]
分类直线:-1.0922787897353627x1+5.193933943326238x2+1.0=0
最少分类错误点的个数:4个

分类直线画图如下：

口袋算法完整代码如下：

import pandas as pd
import matplotlib.pyplot as plt
fig,ax=plt.subplots()
import numpy as np

data=pd.read_csv(r"...\data2.csv",header=None)

X=data.iloc[:,[0,1]]  #提取特征
y=data[2]   #提取目标

###把数据归一化###
mean=X.mean(axis=0)
sigma=X.std(axis=0)
X=(X-mean)/sigma

###提取不同类别的数据，用于画图###
x_positive=X[y==1]
x_negative=X[y==-1]

ax.scatter(x_positive[0],x_positive[1],marker="o",label="y=+1")
ax.scatter(x_negative[0],x_negative[1],marker="x",label="y=-1")
ax.legend()
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_title("standardized Data")

X[2]=np.ones((X.shape[0],1))   #增加一列常数项
X=X.values    #把特征转换成ndarray格式

###初始化w###
w=X[0].copy()  #选取原点到第一个点的向量作为w的初始值
w[2]=0  #增加一项---阈值，阈值初始化为0
w=w.reshape(3,1)

y=y.values.reshape(100,1)  #把目标转换成ndarray格式，形状和预测目标相同

def compare(X,w,y):
    ###用于比较预测目标y_pred和实际目标y是否相符，返回分类错误的地方loc_wrong###
    ###输入特征，权重，目标###
    scores=np.dot(X,w)  #把特征和权重点乘，得到此参数下预测出的目标分数

    y_pred=np.ones((scores.shape[0],1))  #设置预测目标，初始化值全为1，形状和目标分数相同

    loc_negative=np.where(scores<0)[0]  #标记分数为负数的地方
    y_pred[loc_negative]=-1  #使标记为负数的地方预测目标变为-1

    loc_wrong=np.where(y_pred!=y)[0]  #标记分类错误的地方

    return loc_wrong

def update(X,w,y):
    ###用于更新权重w，返回更新后的权重w###
    ###输入特征，权重，目标###
    num=len(compare(X,w,y)) #分类错误点的个数
    w=w+y[compare(X,w,y)][np.random.choice(num)]*X[compare(X,w,y),:][np.random.choice(num)].reshape(3,1)
    return w

def perceptron_pocket(X,w,y):
    ###感知机口袋算法，显示n次迭代后最好的权重和分类直线，并画出分类直线###
    ###输入特征，初始权重，目标###
    best_len=len(compare(X,w,y))  #初始化最少的分类错误点个数
    best_w=w  #初始化口袋里最好的参数w
    for i in range(100):
        print("错误分类点有{}个。".format(len(compare(X,w,y))))
        w=update(X,w,y)
        #如果当前参数下分类错误点个数小于最少的分类错误点个数，那么更新最少的分类错误点个数和口袋里最好的参数w
        if len(compare(X,w,y))<best_len:
            best_len=len(compare(X,w,y))
            best_w=w

    print("参数best_w:{}".format(best_w))
    print("分类直线:{}x1+{}x2+{}=0".format(best_w[0][0],best_w[1][0],best_w[2][0]))
    print("最少分类错误点的个数:{}个".format(best_len))
    line_x=np.linspace(-3,3,10)
    line_y=(-best_w[2]-best_w[0]*line_x)/best_w[1]
    ax.plot(line_x,line_y)

plt.show()

另外附上感知机算法用损失函数和梯度下降法实现的代码（和上述感知机算法的不同之处在于w每次是用离当前分类直线最远的那个分类错误点进行更新的）：

import pandas as pd
import matplotlib.pyplot as plt
fig,ax=plt.subplots()
import numpy as np

data=pd.read_csv(r"...\data1.csv",header=None)

X=data.iloc[:,[0,1]]  #提取特征
y=data[2]   #提取目标

class Perceptron:
    def __init__(self):
        self._w = self._b = None

    def standardization(self,X):
        #将输入的X归一化
        mean=X.mean(axis=0)
        sigma=X.std(axis=0)
        X=(X-mean)/sigma

        return X

    def fit(self, X, y, lr=1, epoch=100):
        #训练数据
        #将输入的X,y转换为numpy数组
        X, y = np.asarray(X, np.float32), np.asarray(y, np.float32)
        #初始化w,b
        self._w = np.zeros(X.shape[1])
        self._b = 0

        for _ in range(epoch):
            # 计算 w·x+b
            y_pred = np.dot(X,self._w) + self._b
            # 标记使损失函数最大的样本
            idx = np.argmax(np.maximum(0, -y_pred * y))
            # 若该样本被正确分类，则结束训练
            if y[idx] * y_pred[idx] > 0:
                break
            # 否则，让参数沿着负梯度方向走一步
            else:
                delta = lr * y[idx]
                self._w += delta * X[idx]
                self._b += delta

        return self._w,self._b

    def print_results(self,w,b):
        print("参数w:{}".format(w))
        print("参数b:{}".format(b))
        print("分类直线:{}x1+{}x2+{}=0".format(w[0],w[1],b))

    def draw_pics(self,X,w,b):
        #提取不同分类的数据
        x_positive=X[y==1]
        x_negative=X[y==-1]

        #画出归一化后的数据
        ax.scatter(x_positive[0],x_positive[1],marker="o",label="y=+1")
        ax.scatter(x_negative[0],x_negative[1],marker="x",label="y=-1")
        ax.legend()
        ax.set_xlabel("x1")
        ax.set_ylabel("x2")
        ax.set_title("Standardized Data")

        #画出分类直线
        line_x=np.linspace(-3,3,10)
        line_y=(-b-w[0]*line_x)/w[1]
        ax.plot(line_x,line_y)

    def predict(self,X):
        return np.where(np.dot(X,self._w)-self._b>0,1,-1)

if __name__=="__main__":
    PLA=Perceptron()
    X=PLA.standardization(X)
    w,b=PLA.fit(X,y,lr=1,epoch=100)
    PLA.print_results(w,b)
    PLA.draw_pics(X,w,b)