hdu 1052 Tian Ji -- The Horse Racing (田忌赛马)

Tian Ji -- The Horse Racing

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 37056    Accepted Submission(s): 11153

Problem Description

Here is a famous story in Chinese history.

"That was about 2300 years ago. General Tian Ji was a high official in the country Qi. He likes to play horse racing with the king and others."

"Both of Tian and the king have three horses in different classes, namely, regular, plus, and super. The rule is to have three rounds in a match; each of the horses must be used in one round. The winner of a single round takes two hundred silver dollars from the loser."

"Being the most powerful man in the country, the king has so nice horses that in each class his horse is better than Tian's. As a result, each time the king takes six hundred silver dollars from Tian."

"Tian Ji was not happy about that, until he met Sun Bin, one of the most famous generals in Chinese history. Using a little trick due to Sun, Tian Ji brought home two hundred silver dollars and such a grace in the next match."

"It was a rather simple trick. Using his regular class horse race against the super class from the king, they will certainly lose that round. But then his plus beat the king's regular, and his super beat the king's plus. What a simple trick. And how do you think of Tian Ji, the high ranked official in China?"

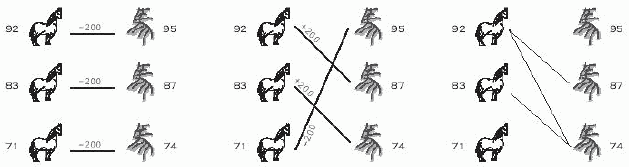
Were Tian Ji lives in nowadays, he will certainly laugh at himself. Even more, were he sitting in the ACM contest right now, he may discover that the horse racing problem can be simply viewed as finding the maximum matching in a bipartite graph. Draw Tian's horses on one side, and the king's horses on the other. Whenever one of Tian's horses can beat one from the king, we draw an edge between them, meaning we wish to establish this pair. Then, the problem of winning as many rounds as possible is just to find the maximum matching in this graph. If there are ties, the problem becomes more complicated, he needs to assign weights 0, 1, or -1 to all the possible edges, and find a maximum weighted perfect matching...

However, the horse racing problem is a very special case of bipartite matching. The graph is decided by the speed of the horses --- a vertex of higher speed always beat a vertex of lower speed. In this case, the weighted bipartite matching algorithm is a too advanced tool to deal with the problem.

In this problem, you are asked to write a program to solve this special case of matching problem.

 

Input

The input consists of up to 50 test cases. Each case starts with a positive integer n (n <= 1000) on the first line, which is the number of horses on each side. The next n integers on the second line are the speeds of Tian’s horses. Then the next n integers on the third line are the speeds of the king’s horses. The input ends with a line that has a single 0 after the last test case.

 

Output

For each input case, output a line containing a single number, which is the maximum money Tian Ji will get, in silver dollars.

 

Sample Input

3
92 83 71
95 87 74
2
20 20
20 20
2
20 19
22 18
0

 

Sample Output

200
0
0

 

 

题目大意：

田忌和齐威王赛马。两人各有n匹马。每匹马都有一个速度属性。赛马时如果平局则不计分，如果赢了记200分，如果输了扣200分。问怎样匹配田忌分最高，输出最高分。

 

贪心好题。

首先比较田忌和齐威王最慢的马，分别为T和Q。

如果T快，则让T赢Q。因为田忌的马都能赢Q，所以用最少的耗费赢Q；

如果T慢，则让T输给齐威王最快的马。因为齐威王的马都能赢T，所以拉齐威王最快的马下水；

如果T和Q一样快，则比较田忌和齐威王最快的马，分别为TT和QQ：

如果TT快，则让TT赢QQ，因为赢谁都是赢，所以赢齐威王最快的马；

如果TT慢，则让QQ赢田忌最慢的马，因为谁输QQ都是输，用最小的耗费输给他；

如果TT和QQ一样快，则让T输给QQ，因为让T、TT平Q、QQ，则田忌并不赚，用T输给QQ，再用一个较小的数赢Q，则田忌省下了TT，稳赚。

 

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<stack>

typedef long long lol;

using namespace std;

const int maxn=;

int a[maxn+];
int b[maxn+];

int main()
{
    int n;
    while(scanf("%d",&n),n)
    {
        for(int i=;i<=n;i++)
            scanf("%d",a+i);
        for(int i=;i<=n;i++)
            scanf("%d",b+i);
        sort(a+,a++n);
        sort(b+,b++n);

        int win=,tie=,los=;
        int a1=,b1=,a2=n,b2=n;
        while(a1<=a2)
        {
            if(a[a1]>b[b1])
            {
                win++;
                a1++;b1++;
            }
            else if(a[a1]<b[b1])
            {
                los++;
                a1++;b2--;
            }
            else
            {
                if(a[a2]>b[b2])
                {
                    win++;
                    a2--;b2--;
                }
                else if(a[a2]<b[b2])
                {
                    los++;
                    a1++;b2--;
                }
                else
                {
                    if(a[a1]<b[b2])
                    {
                        los++;
                        a1++;b2--;
                    }
                    else
                    {
                        tie++;
                        a1++;b2--;
                    }
                }
            }
        }

        printf("%d\n",win*-los*);
    }
    return ;
}