多源最短路径算法—Floyd算法

前言

在图论中，在寻路最短路径中除了Dijkstra算法以外，还有Floyd算法也是非常经典，然而两种算法还是有区别的，Floyd主要计算多源最短路径。

在单源正权值最短路径，我们会用Dijkstra算法来求最短路径，并且算法的思想很简单——贪心算法:每次确定最短路径的一个点然后维护(更新)这个点周围点的距离加入预选队列，等待下一次的抛出确定。但是虽然思想很简单，实现起来是非常复杂的，我们需要邻接矩阵(表)储存长度，需要优先队列(或者每次都比较)维护一个预选点的集合。还要用一个boolean数组标记是否已经确定、还要---------

总之，Dijkstra算法的思想上是很容易接受的，但是实现上其实是非常麻烦的。但是单源最短路径没有更好的办法。复杂度也为O(n2)

而在n节点多源最短路径中,如果从Dijkstra算法的角度上，只需要将Dijkstra封装，然后执行n次Dijkstra算法即可,复杂度为O(n3)。但是这样感觉很臃肿，代码量巨大，占用很多空间内存。有没有啥方法能够稍微变变口味呢？

答案是有的，这就是易写但稍需要理解的Floyd算法。一个求多元最短路径算法。

算法介绍

先看看百度百科的定义吧：

Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

简单的来说，算法的主要思想是动态规划(dp)，而求最短路径需要不断松弛(熟悉spfa算法的可能熟悉松弛)。

而算法的具体思想为：

1. 邻接矩阵dist储存路径，同时最终状态代表点点的最短路径。如果没有直接相连的两点那么默认为一个很大的值(不要溢出)！而自己的长度为0.
2. 从第1个到第n个点依次加入图中。每个点加入进行试探是否有路径长度被更改。
3. 而上述试探具体方法为遍历图中每一个点(i,j双重循环)，判断每一个点对距离是否因为加入的点而发生最小距离变化。如果发生改变，那么两点(i,j)距离就更改。
4. 重复上述直到最后插点试探完成。

其中第三步的状态转移方程为:

• dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])
  
  其中dp[x][y]的意思可以理解为x到y的最短路径。所以dp[i][k]的意思可以理解为i到k的最短路径dp[k][j]的意思可以理解为k到j的最短路径.

咱们图解一个案例：



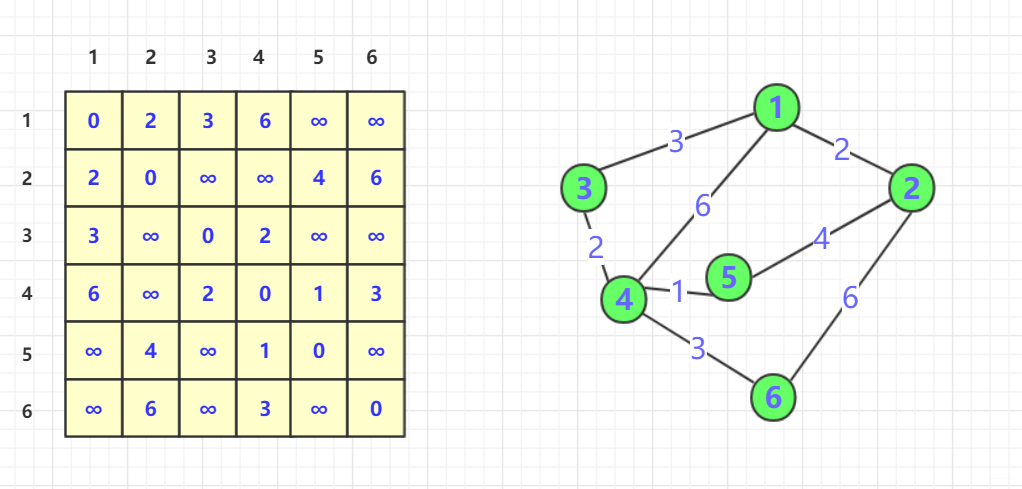
默认的最短长度初始为邻接矩阵初始状态

• 加入第一个节点1,大家可以发现，由于1的加入，使得本来不连通的2，3点对和2，4点对变得联通，并且加入1后距离为当前最小。(可以很直观加入5之后2，4，更短但是还没加入)。为了更好的描述其实此时的直接联通点多了两条。(2,3)和(2,4).我们在dp中不管这个结果是通过前面那些步骤来的，但是在这个状态，这两点的最短距离就算它！
  
  
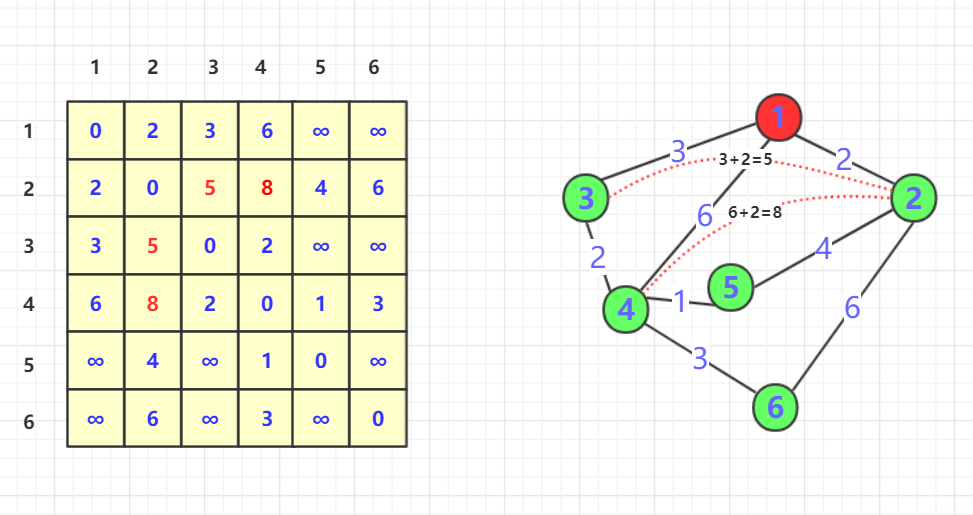
• 同时你可以发现加入1其中也使得3,1,4这样联通，但是 3,1,4联通的话距离为9远远大于本来的(3,4)为2，所以不进行更新。
• 咱们继续加入第二个节点。在加入的初始态为：
  
  
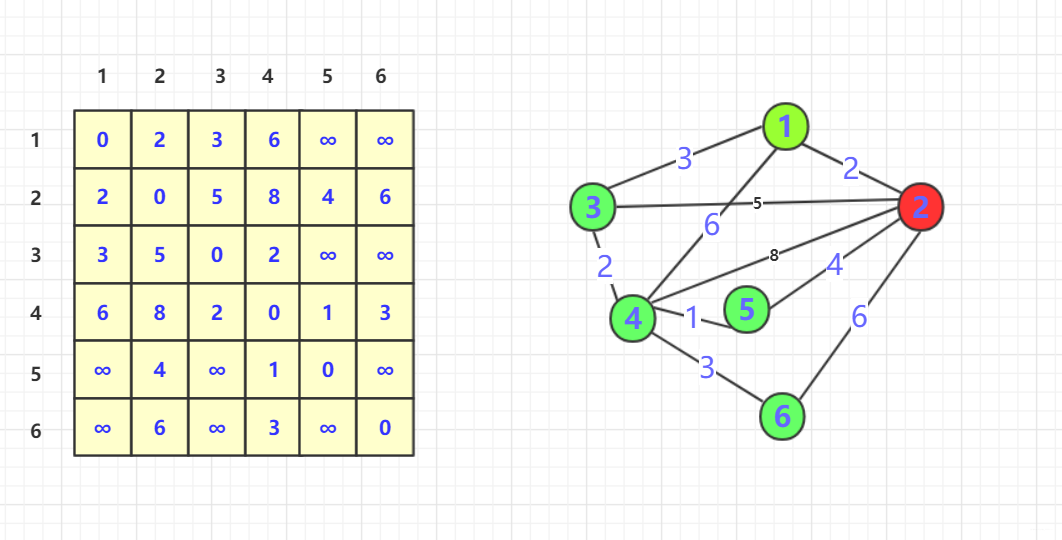
• 进行遍历插入看看是否更新节点
  
  
  
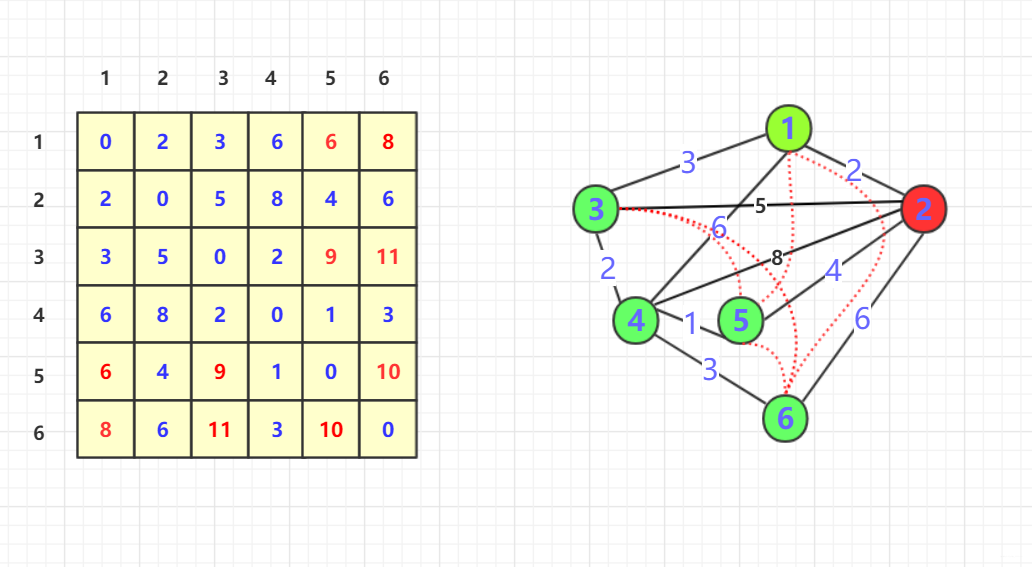
  实际上这个时候图中的连线就比较多了。当然这些连线都是代表当前的最短路径。 这也和我们的需求贴合，我们最终要的是所有节点的最短路径。每个节点最终都应该有6条指向不同节点的边！ 表示邻接矩阵的最终结果。

至于算法的模拟两部核心已经告诉大家了，大家可以自行模拟剩下的。

程序实现

而对于程序而言，这个插入的过程相当简单。核心代码只有四行！

代码如下

public class floyd {
	static int max = 66666;// 别Intege.max 两个相加越界为负
	public static void main(String[] args) {
		int dist[][] = {
				{ 0, 2, 3, 6, max, max },
				{ 2, 0, max, max,4, 6 },
				{ 3, max, 0, 2, max, max },
				{ 6, max, 2, 0, 1, 3 },
				{ max, 4, max, 1, 0, max },
				{ max, 6, max, 3, max, 0 } };// 地图
		// 6个
		for (int k = 0; k < 6; k++)// 加入滴k个节点
		{
			for (int i = 0; i < 6; i++)// 松弛I行
			{
				for (int j = 0; j < 6; j++)// 松弛i列
				{
					dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
				}
			}
		}
		// 输出
		for (int i = 0; i < 6; i++) {
			System.out.print("节点"+(i+1)+" 的最短路径");
			for (int j = 0; j < 6; j++) {
				System.out.print(dist[i][j]+" ");
			}
			System.out.println();
		}
	}
}

结果为：



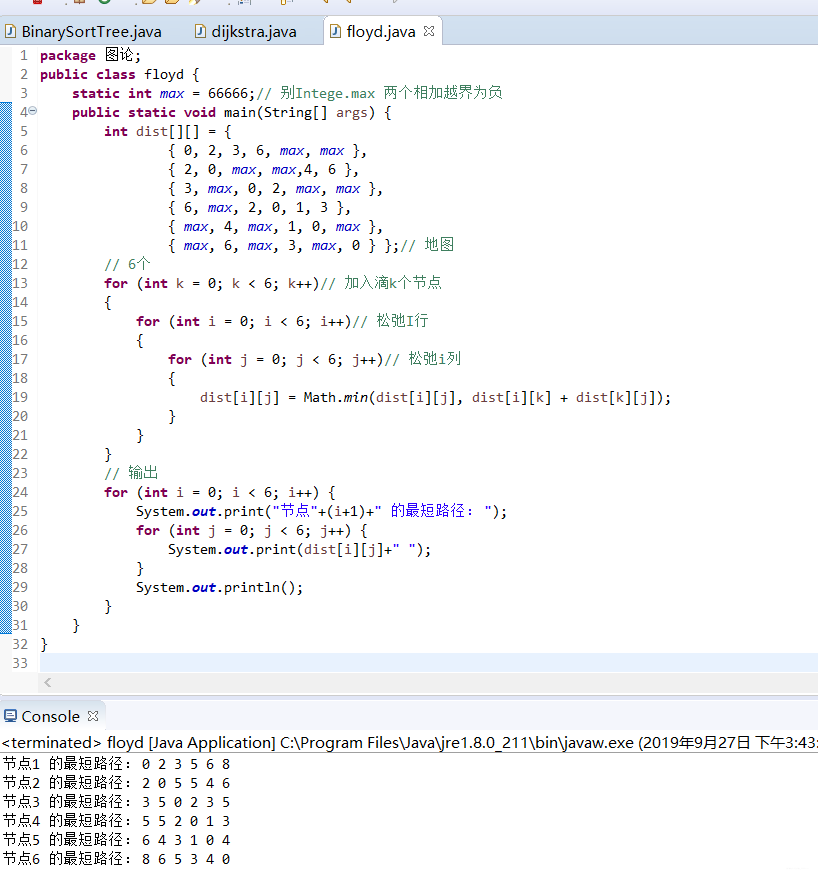
可以自行计算，图和上篇的Dijkstra是一致的，大家可以自行比对，结果一致，说明咱么的结果成功的。

当然，在你学习的过程中，可以在每加入一个节点插入完成后，打印邻接矩阵的结果，看看前两部和笔者的是否相同(有助于理解)，如果相同，则说明正确！

你可能还会有疑惑，那咱么就用一个局部性来演示一下，看其中AB最短距离变化情况祝你理解：

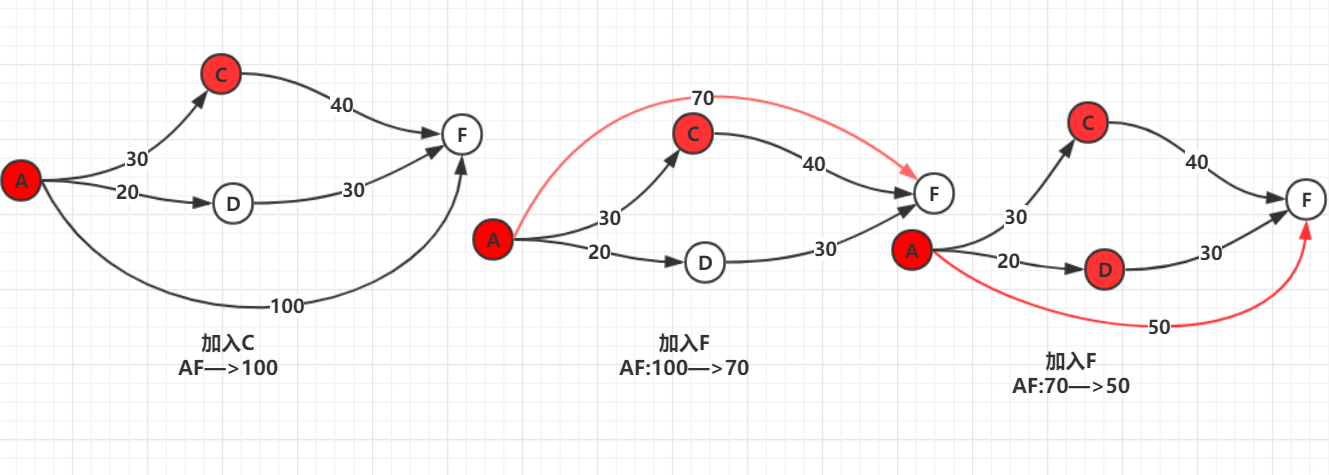
好啦，Floyd算法就介绍到这里，如果对你有帮助，请动动小手点个赞吧！蟹蟹。

希望和各位共同进步！欢迎关注笔者公众号：bigsai!