剑指offer-36：数组中的逆序对

参考：1、 https://www.geeksforgeeks.org/merge-sort/

2、《剑指Offer：名企面试官精讲典型编程题》

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

输入描述:

题目保证输入的数组中没有的相同的数字

数据范围：

• 对于%50的数据,size<=10^4
• 对于%75的数据,size<=10^5
• 对于%100的数据,size<=2*10^5

示例1
输入：1，2，3，4，5，6，7，0
输出：7

解题思路1 （暴力法，时间复杂度: O(n^2)）

这个方法最简单直接，顺序扫描整个数组，每扫到一个数，逐个比较其后面的所有数，如果构成逆序对，则计数+1。代码没啥难度，略了。

解题思路2 （分治法，时间复杂度: O(nlogn)，空间复杂度：O(n)）

     public int InversePairs(int[] array) {
         if (array.length < 2) {
             return 0;
         }
         return divideAndConquer(array, 0, array.length);
     }

     public int divideAndConquer(int[] array, int l, int r) {
         if (l >= r - 1) return 0;

         int mid = (l + r) / 2;
         int count = 0;
         int countL = divideAndConquer(array, l, mid);
         int countR = divideAndConquer(array, mid, r);
         int[] left = Arrays.copyOfRange(array, l, mid);
         int[] right = Arrays.copyOfRange(array, mid, r);
         int i = left.length - 1;
         int j = right.length - 1;
         for (int k = r - 1; k >= l; k--) {
             // two cases: left is empty or right is empty
             if (i < 0) {
                 array[k] = right[j];
                 j--;
                 continue;
             } else if (j < 0) {
                 array[k] = left[i];
                 i--;
                 continue;
             }
             if (left[i] > right[j]) {
                 count += j + 1;
                 if (count > 1000000007) {
                     count %= 1000000007;
                 }
                 array[k] = left[i];
                 i--;
             } else {
                 array[k] = right[j];
                 j--;
             }
         }
         return (count + countL + countR) % 1000000007;
     }

这一题的解法是在归并排序(Merge Sort) 的基础上修改得到的。Merge Sort使用的是分治法的思想。分治法 (divide and conquer) 是将一个复杂的问题，分成两个或多个相同或者相似的子问题，再把子问题分成更小的子问题，一直分到子问题足够简单来求解，最后再把子问题的解合并成原问题的解。归并排序法的时间复杂度为 O(nlogn)，空间复杂度为 临时的数组 + 递归时压入栈的数据占用的空间 = n + logn，即 O(n)。

以数组 {7, 5, 6, 4} 为例进行分析，解题过程如图5.2所示。首先将数组拆成至长度为1的子数组，然后一边合并一边统计逆序对的数目。在第一对长度为1 的子数组 {7}、{5}中，有一对逆序对 (7, 5)。在第二对长度为1的子数组 {6}、{4}中，也有一对逆序对(6, 4)。在统计完这两对逆序对后，需要分别对他们进行排序，如图 5.2(c)，以免在以后的统计过程中再重复统计。

然后需要统计两个长度为2的子数组之间的逆序对，并合并两个子数组，如图5.3所示。两个子数组分别从末尾开始判断数的大小，如图5.2(a)中指针P1、P2。如果 P1 大于 P2，则构成逆序对，并且逆序对的数目等于第二个子数组中剩余数字的个数，即 P2 以及之前的所有数字的个数。如果 P1 小于或等于 P2, 则不构成逆序对。每次比较的时候，我们都把较大的数字从后往前复制到一个辅助数组，确保辅助数组中的数字是递增排序的。在把较大的数字复制到辅助数组之后，把对应的指针向前移动一位，接下来进行下一轮比较。

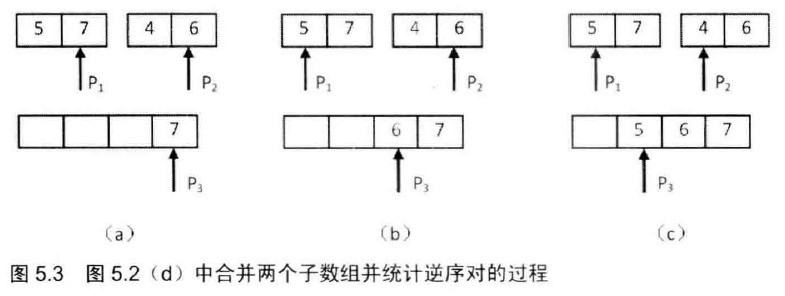
以此类推，使用这个方法去求出其他数组的逆序对个数。在解这一题的时候，还有一点需要注意，除了需要将总输出结果 (count + countL + countR) 对1000000007取模，还要在计算过程中将 count += j + 1 对1000000007取模，以免count超出 Integer.MAX_VALUE。