codeforces 572 D. Minimization（dp+ 思维）

题目链接：http://codeforces.com/contest/572/problem/D

题意：给出一个序列，可以任意调整序列的顺序，使得给出的式子的值最小

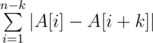
题解：显然要先排一下序，然后取相邻的显然是和最小的。要知道取完整条链之后的，值为

a[n]-a[1]-（没连在一起的a[k+1]-a[k]的值），一遍遍历下来肯定能得到2种长度的链。

len1=n/k+1,len2=n/k,count1=n%k,count2=k-count1,(count1表示长度为len1的链有几条

count2表示长度为len2的链有几条)。这样就有方向了，只要求那些没连在一起的a[k+1]-a[k]的最大值

即可。

设dp[i][j]表示有i条长度为len1的，j条长度为len2的链，没连在一起的a[k+1]-a[k]的最大值

显然转移方程为

pos = (i - 1) * len1 + j * len2;

dp[i][j] = max(dp[i][j] , dp[i - 1][j] + a[pos + 1] - a[pos])

pos = i * len1 + (j - 1) * len2;

dp[i][j] = max(dp[i][j] , dp[i][j - 1] + a[pos + 1] - a[pos]);

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
using namespace std;
const int M = 3e5 + 10;
int a[M] , dp[5010][5010];
int main() {
    int n , k;
    scanf("%d%d" , &n , &k);
    for(int i = 1 ; i <= n ; i++) {
        scanf("%d" , &a[i]);
    }
    sort(a + 1 , a + n + 1);
    a[0] = a[1] , a[n + 1] = a[n];
    int len1 = n / k + 1 , len2 = n / k;
    int count1 = n % k , count2 = k - count1;
    memset(dp , 0 , sizeof(dp));
    for(int i = 0 ; i <= count1 ; i++) {
        for(int j = 0 ; j <= count2 ; j++) {
            if(i) {
                int pos = (i - 1) * len1 + j * len2;
                dp[i][j] = max(dp[i][j] , dp[i - 1][j] + a[pos + 1] - a[pos]);
            }
            if(j) {
                int pos = i * len1 + (j - 1) * len2;
                dp[i][j] = max(dp[i][j] , dp[i][j - 1] + a[pos + 1] - a[pos]);
            }
        }
    }
    int ans = a[n] - a[1] - dp[count1][count2];
    printf("%d\n" , ans);
    return 0;
}