【Windows Of CCPC HDU - 6708】【打表，找规律】

题意分析

HDU - 6708

题意：给出一个整数k，要求你输出一个长和宽均为2^k 的符合要求的矩阵。比如k等于1时输出

\[ \begin{matrix}
C & C \\
P & C
\end{matrix}
$$k = 2时输出
\]

\begin{matrix}

C & C & C & C \

P & C & P & C \

P & P & C & C \

C & P & P & C

\end{matrix}

\[样例乍一看好像是第一个矩阵规定为k=1这种样子，后一个矩阵则以前一个矩阵为基础，可以将矩阵平分为四块(竖着切和横着切)，每一部分正好对应前一个矩阵的整体，只有左下角那一块例外，对应的是前一块矩阵的”反面“（也就是C变为P，P变为C），不过这样仍然没有什么思路，后来观察发现上一块矩阵的某一个元素刚好对应下一个矩阵的某一块元素，比如对于字母C，有

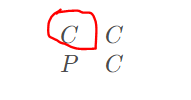
对应下一个矩阵的

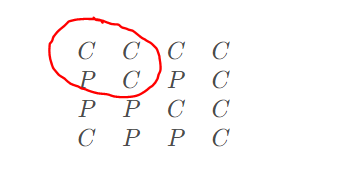
对于字母P，有

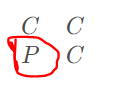
对应下一个矩阵的

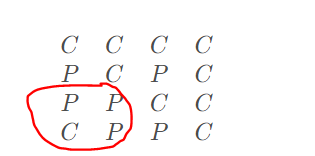
这样根据它们的相对位置，就不难给出所有情况的矩阵了。具体位置关系在代码中给出。
## AC代码
关于代码，的确有些冗长，感觉应该有其他更简便方法表示这种规律，欢迎大佬评论指出。

```c
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
using namespace std;
const int maxn = 1024 + 10;
int T, k;
char s1[maxn][maxn], s2[maxn][maxn], s3[maxn][maxn], s4[maxn][maxn], s5[maxn][maxn], s6[maxn][maxn], s7[maxn][maxn], s8[maxn][maxn], s9[maxn][maxn], s10[maxn][maxn];
void init()
{
for(int i = 1; i <= 2; i++)
{
for(int j = 1; j <= 2; j++)
{
if(s1[i][j] == 'C')
{
//规律如下，此后的直接套用即可
for(int k = (j-1)*2+1; k <= (j-1)*2+2; k++)
s2[(i-1)*2+1][k] = 'C';
s2[(i-1)*2+2][(j-1)*2+1] = 'P', s2[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s2[(i-1)*2+1][k] = 'P';
s2[(i-1)*2+2][(j-1)*2+1] = 'C', s2[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 4; i++)
{
for(int j = 1; j <= 4; j++)
{
if(s2[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s3[(i-1)*2+1][k] = 'C';
s3[(i-1)*2+2][(j-1)*2+1] = 'P', s3[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s3[(i-1)*2+1][k] = 'P';
s3[(i-1)*2+2][(j-1)*2+1] = 'C', s3[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 8; i++)
{
for(int j = 1; j <= 8; j++)
{
if(s3[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s4[(i-1)*2+1][k] = 'C';
s4[(i-1)*2+2][(j-1)*2+1] = 'P', s4[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s4[(i-1)*2+1][k] = 'P';
s4[(i-1)*2+2][(j-1)*2+1] = 'C', s4[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 16; i++)
{
for(int j = 1; j <= 16; j++)
{
if(s4[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s5[(i-1)*2+1][k] = 'C';
s5[(i-1)*2+2][(j-1)*2+1] = 'P', s5[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s5[(i-1)*2+1][k] = 'P';
s5[(i-1)*2+2][(j-1)*2+1] = 'C', s5[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 32; i++)
{
for(int j = 1; j <= 32; j++)
{
if(s5[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s6[(i-1)*2+1][k] = 'C';
s6[(i-1)*2+2][(j-1)*2+1] = 'P', s6[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s6[(i-1)*2+1][k] = 'P';
s6[(i-1)*2+2][(j-1)*2+1] = 'C', s6[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 64; i++)
{
for(int j = 1; j <= 64; j++)
{
if(s6[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s7[(i-1)*2+1][k] = 'C';
s7[(i-1)*2+2][(j-1)*2+1] = 'P', s7[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s7[(i-1)*2+1][k] = 'P';
s7[(i-1)*2+2][(j-1)*2+1] = 'C', s7[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 128; i++)
{
for(int j = 1; j <= 128; j++)
{
if(s7[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s8[(i-1)*2+1][k] = 'C';
s8[(i-1)*2+2][(j-1)*2+1] = 'P', s8[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s8[(i-1)*2+1][k] = 'P';
s8[(i-1)*2+2][(j-1)*2+1] = 'C', s8[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 256; i++)
{
for(int j = 1; j <= 256; j++)
{
if(s8[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s9[(i-1)*2+1][k] = 'C';
s9[(i-1)*2+2][(j-1)*2+1] = 'P', s9[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s9[(i-1)*2+1][k] = 'P';
s9[(i-1)*2+2][(j-1)*2+1] = 'C', s9[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
for(int i = 1; i <= 512; i++)
{
for(int j = 1; j <= 512; j++)
{
if(s9[i][j] == 'C')
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s10[(i-1)*2+1][k] = 'C';
s10[(i-1)*2+2][(j-1)*2+1] = 'P', s10[(i-1)*2+2][(j-1)*2+2] = 'C';
}
else
{
for(int k = (j - 1)*2+1; k <= (j-1)*2+2; k++)
s10[(i-1)*2+1][k] = 'P';
s10[(i-1)*2+2][(j-1)*2+1] = 'C', s10[(i-1)*2+2][(j-1)*2+2] = 'P';
}
}
}
}
int main()
{
// freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
memset(s1, 'C', sizeof(s1));
cin >> T;
s1[2][1] = 'P';
init();
while(T--)
{
cin >> k;
for(int i = 1; i <= (int)(pow(2, k)); i++)
{
for(int j = 1; j <= (int)(pow(2, k)); j++)
{
if(k == 1)
cout << s1[i][j];
else if(k == 2)
cout << s2[i][j];
else if(k == 3)
cout << s3[i][j];
else if(k == 4)
cout << s4[i][j];
else if(k == 5)
cout << s5[i][j];
else if(k == 6)
cout << s6[i][j];
else if(k == 7)
cout << s7[i][j];
else if(k == 8)
cout << s8[i][j];
else if(k == 9)
cout << s9[i][j];
else if(k == 10)
cout << s10[i][j];
}
cout << endl;
}
}
}
```\]