166. 数独 dancing links 方法

dfs硬怼通过数独 N皇后的代码后 想学习下新的数据结构和算法来解决这类覆盖问题

习题练习

https://www.acwing.com/problem/content/168/ 数独

https://www.acwing.com/problem/content/171/ 数独2

https://www.acwing.com/problem/content/185/ 靶形数独

资料收集如下 进行学习

https://www.cnblogs.com/ivan-count/p/7355431.html

https://www.cnblogs.com/grenet/p/3145800.html

https://blog.csdn.net/whereisherofrom/article/details/79220897

习题学习

洛谷

https://www.luogu.org/problem/P4929  P4929 【模板】舞蹈链（DLX）

https://www.luogu.org/problem/P1074  P1074 靶形数独

https://www.luogu.org/problem/P1219  P1219 八皇后

题解

https://www.luogu.org/blog/ONE-PIECE/qian-tan-dlx  【模板】舞蹈链（DLX）

https://www.luogu.org/blog/ONE-PIECE/ba-xing-shuo-du-dai-ma  靶形数独

https://www.luogu.org/blog/ONE-PIECE/solution-p1219 八皇后

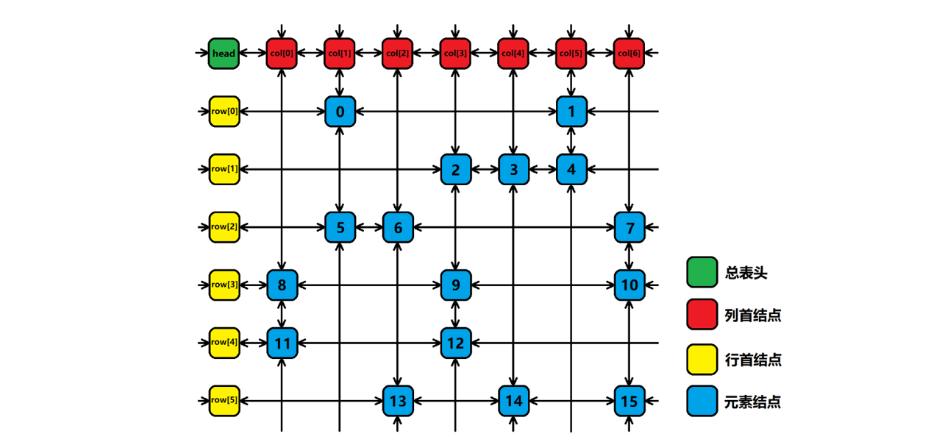
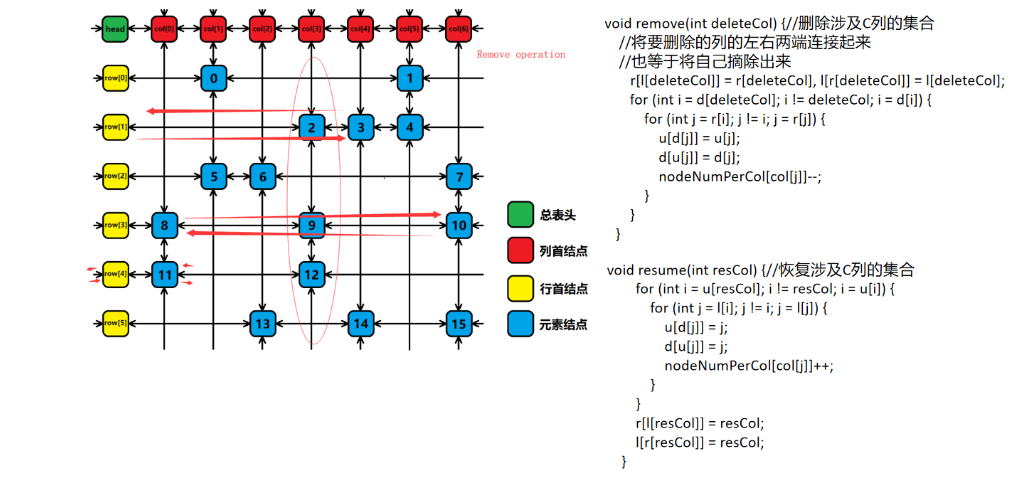
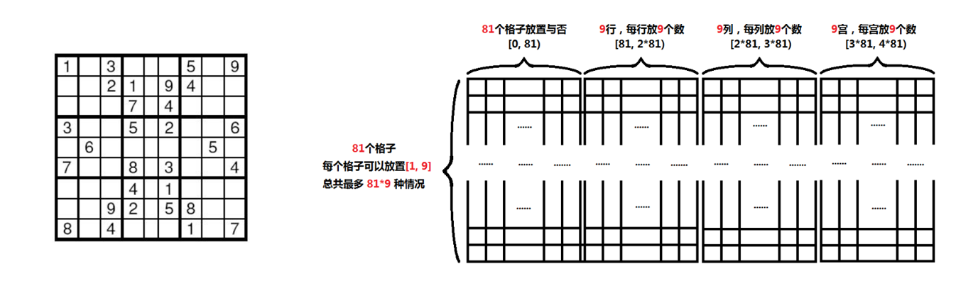
我的对模板注释的代码  参考的源代码地址https://www.luogu.org/blog/ONE-PIECE/qian-tan-dlx

 #include <iostream>
 #include <stdio.h>
 #include <string.h>  

 //精确覆盖问题的定义：给定一个由0-1组成的矩阵，是否能找到一个行的集合，使得集合中每一列都恰好包含一个1
 const int MN =  *  *  + ;//最大行数,共有9*9个格子，每个格子可以放1~9
 const int MM =  *  +  *  +  *  +  *  + ;//最大列数
 const int MAX_NUM = MN * MM; //最大点数  

 struct DLX
 {
     int n, m, idx;//n行数m列数idx 元素索引
                  //十字链表组成部分  

     int l[MAX_NUM], r[MAX_NUM], u[MAX_NUM], d[MAX_NUM];    //记录某个idx索引点的上下左右点的索引
     int col[MAX_NUM], row[MAX_NUM];    //两者结合使用 记录某个idx索引点的行 列号

     int nodeIdxPerRow[MAX_NUM];        //记录每行的开头节点的索引
     int nodeNumPerCol[MAX_NUM];        //记录每列节点的个数

     int ansd, ans[MN];

     void init(int n ,int m)    //初始化十字链表的 头节点和 列节点表头串   m表示有多少列
     {
         //初始化头结点和 列节点表头串 头节点数组索引 = 0  列节点表头共m个 索引 1~m
         for (int i = ; i <= m; i++) {
             r[i] = i + ;
             l[i] = i - ;
             u[i] = d[i] = i;    //列节点头串只有互相横向连接 上下连接均指向自己
         }
         r[m] = ;
         l[] = m;  //循环连接 col[m] 的右端指向头节点 头结点的左端指向clo[m]

         memset(nodeIdxPerRow, , sizeof(nodeIdxPerRow));
         memset(nodeNumPerCol, , sizeof(nodeNumPerCol));

         idx = m + ; //目前使用 0 头结点 与 m个列节点表头串 0~m 共m+1个节点
     }

     //插入节点 进行的一些数据记录
     void link(int insertRow, int insertCol)
     {
         nodeNumPerCol[insertCol]++; //插入一个节点 那么该列的节点个数+1
         row[idx] = insertRow;
         col[idx] = insertCol;    //记录第idx个节点所在的行与列

         u[idx] = insertCol;    //当前插入的节点索引记录 向上指向列节点头串中的insertCol
         d[idx] = d[insertCol];    //当前插入节点索引记录 向下指向原来列节点头串的向下指向点
         u[d[insertCol]] = idx;    //原来列节点头串指向的节点 向上由指向列节点头串指向插入的节点(使用索引)
         d[insertCol] = idx;        //列节点头串则向下指向新插入的节点(使用索引)

         //更新每行的节点记录  nodeIdxPerRow
         if (nodeIdxPerRow[insertRow] == ) {
             //如果该节点是第一个插入的节点
             nodeIdxPerRow[insertRow] = r[idx] = l[idx] = idx;//该行没有点，直接加入
         }
         else {
             //如果不是第一个插入的节点 同上面处理列次序一样 在记录和第一个节点间 插入本函数插入的节点
             r[idx] = nodeIdxPerRow[insertRow];        //新节点的右端指向原来行记录中的第一个节点
             l[idx] = l[nodeIdxPerRow[insertRow]];    //新节点的左端指向原来行记录第一个节点的左端 也就是行记录nodeIdxPerRow
             r[l[nodeIdxPerRow[insertRow]]] = idx;    //原来行记录第一个节点的左端(也就是行记录nodeIdxPerRow)的右端 指向新插入的点(使用索引)
             l[nodeIdxPerRow[insertRow]] = idx;        //原来行记录第一个节点的左端指向新插入的节点(使用索引)

         }
         idx++;
         return;
     }

     void remove(int deleteCol) {//删除涉及C列的集合
      //将要删除的列的左右两端连接起来 也等于将自己摘除出来
         r[l[deleteCol]] = r[deleteCol], l[r[deleteCol]] = l[deleteCol];
         for (int i = d[deleteCol]; i != deleteCol; i = d[i]) {
             for (int j = r[i]; j != i; j = r[j]) {
                 u[d[j]] = u[j];
                 d[u[j]] = d[j];
                 nodeNumPerCol[col[j]]--;
             }
         }
     }
     void resume(int resCol) {//恢复涉及C列的集合
         for (int i = u[resCol]; i != resCol; i = u[i]) {
             for (int j = l[i]; j != i; j = l[j]) {
                 u[d[j]] = j;
                 d[u[j]] = j;
                 nodeNumPerCol[col[j]]++;
             }
         }
         r[l[resCol]] = resCol;
         l[r[resCol]] = resCol;
     }

     bool dance(int deep) //选取了d行
     {
         if (r[] == )//全部覆盖了
         {
             //全覆盖了之后的操作
             ansd = deep;
             return ;
         }

         int c = r[];//表头结点指向的第一个列
         for (int i = r[]; i != ; i = r[i])//枚举列头指针
         {
             if (nodeNumPerCol[i] < nodeNumPerCol[c])c = i;

         }

         remove(c);//将该列删去
         for (int i = d[c]; i != c; i = d[i])
         {//枚举该列的元素
             ans[deep] = row[i];//记录该列元素的行
             for (int j = r[i]; j != i; j = r[j])
                 remove(col[j]);//将该列的某个元素的行上的元素所在的列都删去
             if (dance(deep + ))
                 return ;
             for (int j = l[i]; j != i; j = l[j])
                 resume(col[j]);
         }
         resume(c);
         return ;
     }
 }dlx;
 //==========================================================

 char s[], path[];
 struct node
 {
     int r, c, v;
 }nds[MN];
 int main()
 {
     while (~scanf("%s", s))
     {
         if (s[] == 'e')break;
         dlx.init( *  * ,  *  * );
         int r = ;
         for (int i = ; i <= ; i++)
         {
             for (int j = ; j <= ; j++)
             {
                 if (s[(i - ) *  + j - ] == '.')
                 {
                     for (int z = ; z <= ; z++)
                     {
                         dlx.link(r, (i - ) *  + j);
                         dlx.link(r,  + (i - ) *  + z);
                         dlx.link(r,  + (j - ) *  + z);
                         dlx.link(r,  + (((i - ) / ) *  + (j + ) /  - ) *  + z);
                         nds[r].r = i, nds[r].c = j, nds[r].v = z;
                         r++;
                     }
                 }
                 else
                 {
                     int z = s[(i - ) *  + j - ] - '';
                     dlx.link(r, (i - ) *  + j);
                     dlx.link(r,  + (i - ) *  + z);
                     dlx.link(r,  + (j - ) *  + z);
                     dlx.link(r,  + (((i - ) / ) *  + (j + ) /  - ) *  + z);
                     nds[r].r = i, nds[r].c = j, nds[r].v = z;
                     r++;
                 }
             }
         }
         dlx.ansd = -;
         dlx.dance();
         int deep = dlx.ansd;
         for (int i = ; i < deep; i++)
         {
             int posr = dlx.ans[i];
             path[(nds[posr].r - ) *  + nds[posr].c - ] = '' + nds[posr].v;
         }
         path[deep] = '\0';
         printf("%s\n", path);
     }
     return ;
 }