洛谷P2414 - [NOI2011]阿狸的打字机

Portal

Description

首先给出一个只包含小写字母和'B'、'P'的操作序列\(s_0(|s_0|\leq10^5)\)。初始时我们有一个空串\(t\)，依次按\(s_0\)的每一位进行操作：

• 如果是小写字母，则在\(t\)后面加入这个小写字母；
• 如果是'B'，则删除\(t\)的最后一位；
• 如果是'P'，则复制t到集合\(S\)中。

操作结束后，集合中有\(n(n\leq10^5)\)个字符串，将它们按加入集合的顺序标号为\(1..n\)。接下来\(m(m\leq10^5)\)次询问，每次询问串\(x\)在串\(y\)中出现了几次。

Solution

首先根据\(s_0\)我们可以方便的建出一棵Trie树并建立fail指针，记录代表串\(x\)的节点为\(end[x]\)。然后我们就得到了一个fail树：



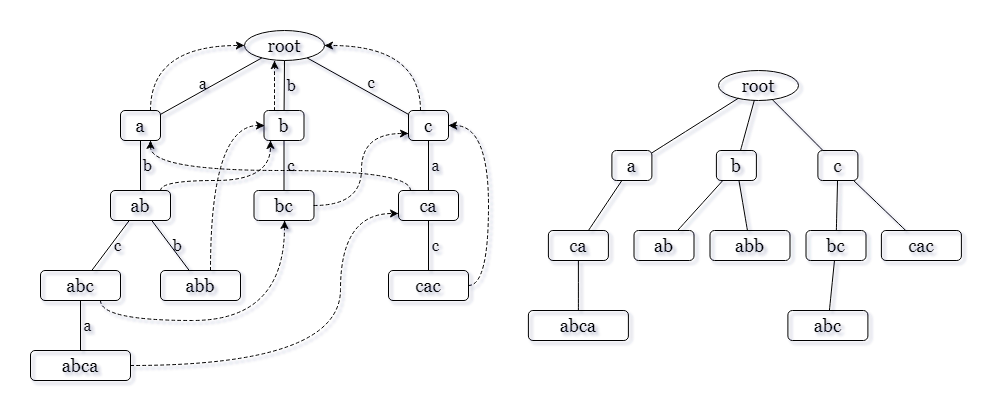
一个节点在fail树上的祖先就是它的一个后缀，子树就是以该节点作为后缀的串。那么询问就相当于“求\(end[x]\)的子树中，有多少个点在\(root\)到\(end[y]\)的路径上”。

我们求出fail树的DFS序，然后将询问按\(y\)排序。用树状数组维护每个点是否被标记，当\(y\)转移到\(y+1\)时，按照建立Trie树的方法转移。求\(end[x]\)的子树中有多少个被标记的点就相当于求DFS序的区间和。

时间复杂度\(O(nlogn+mlogn)\)。

Code

//[NOI2011]阿狸的打字机
#include <algorithm>
#include <cstdio>
using std::sort;
int const N=1e5+10;
int n; char s0[N];
struct query{int id,x,y,ans;} q[N];
bool cmpY(query x,query y) {return x.y<y.y;}
bool cmpID(query x,query y) {return x.id<y.id;}
int rt,ndCnt,fa[N],ch[N][26],fail[N]; int end[N];
int Q[N],op,cl;
int edCnt,h[N];
struct edge{int v,nxt;} ed[N];
void edAdd(int u,int v)
{
    fail[v]=u;
    edCnt++; ed[edCnt].v=v,ed[edCnt].nxt=h[u],h[u]=edCnt;
}
void bldFail()
{
    for(int i=0;i<26;i++) ch[0][i]=rt;
    Q[++cl]=rt;
    while(op<cl)
    {
        int p=Q[++op];
        for(int i=0;i<26;i++)
        {
            int q=ch[p][i];
            if(!q) ch[p][i]=ch[fail[p]][i];
            else edAdd(ch[fail[p]][i],q),Q[++cl]=q;
        }
    }
}
int dfCnt,fr[N],to[N];
void dfs(int u)
{
    dfCnt++; fr[u]=dfCnt;
    for(int i=h[u];i;i=ed[i].nxt) dfs(ed[i].v);
    to[u]=dfCnt;
}
int tr[N];
void add(int x,int v) {while(x<=ndCnt) tr[x]+=v,x+=x&(-x);}
int sum(int x) {int r=0; while(x) r+=tr[x],x-=x&(-x); return r;}
int main()
{
    scanf("%s",s0+1);
    rt=++ndCnt;
    for(int i=1,p=rt;s0[i];i++)
    {
        int x=s0[i]-'a';
        if(s0[i]=='B') p=fa[p];
        else if(s0[i]=='P') end[++n]=p;
        else {if(!ch[p][x]) fa[ch[p][x]=++ndCnt]=p; p=ch[p][x];}
    }
    bldFail(); for(int i=1;i<=ndCnt;i++) if(!fr[i]) dfs(i);
    int m; scanf("%d",&m);
    for(int i=1;i<=m;i++) scanf("%d%d",&q[i].x,&q[i].y),q[i].id=i;
    sort(q+1,q+m+1,cmpY);
    int now=0,p=rt;
    for(int i=0,owo=1,no;owo<=m;owo++)
    {
        int x=q[owo].x,y=q[owo].y;
        while(now<y)
        {
            i++;
            if(s0[i]=='B') add(fr[p],-1),p=fa[p];
            else if(s0[i]=='P') now++;
            else p=ch[p][s0[i]-'a'],add(fr[p],1);
        }
        q[owo].ans=sum(to[end[x]])-sum(fr[end[x]]-1);
    }
    sort(q+1,q+m+1,cmpID);
    for(int i=1;i<=m;i++) printf("%d\n",q[i].ans);
    return 0;
}

P.S.

双倍经验BZOJ2434