1047B_Cover Points

B. Cover Points

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

There are nn points on the plane, (x1,y1),(x2,y2),…,(xn,yn)(x1,y1),(x2,y2),…,(xn,yn).

You need to place an isosceles triangle with two sides on the coordinate axis to cover all points (a point is covered if it lies inside the triangle or on the side of the triangle). Calculate the minimum length of the shorter side of the triangle.

Input

First line contains one integer nn (1≤n≤1051≤n≤105).

Each of the next nn lines contains two integers xixi and yiyi (1≤xi,yi≤1091≤xi,yi≤109).

Output

Print the minimum length of the shorter side of the triangle. It can be proved that it's always an integer.

Examples

input

Copy

3
1 1
1 2
2 1

output

Copy

3

input

Copy

4
1 1
1 2
2 1
2 2

output

Copy

4

Note

Illustration for the first example: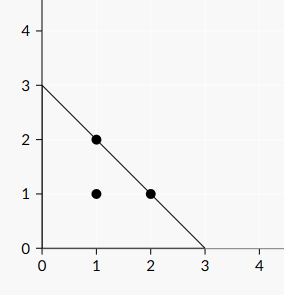

Illustration for the second example: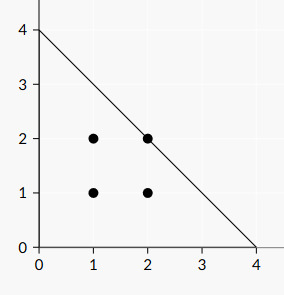

题意：唔就是，让你找到一个最小的等腰三角形，使得给出的所有点都包含在等腰三角形里或者等腰三角形边上

分析:  其实就是找给出的点在y轴上截距最大的时候，满足方程y=-x+b,移一下就是,x+y=b，只要找到x+y的最大值即可、

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 using namespace std;
 int main()
 {
     int n;
     while(~scanf("%d",&n))
     {
         int a,b,ans=;
         while(n--)
         {
             scanf("%d %d",&a,&b);
             ans=max(a+b,ans);
         }
         printf("%d\n",ans);
     }
     return ;
 }