简单prufer应用

【bzoj1005】

Description

　　自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?

Input

　　第一行为N(0 < N < = 1000),
接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1

Output

　　一个整数,表示不同的满足要求的树的个数,无解输出0

Sample Input

3
1
-1
-1

Sample Output

2

关于prufer序列这个定理的证明，

给出大佬博客http://hzwer.com/3272.html

我这里就给一个结论

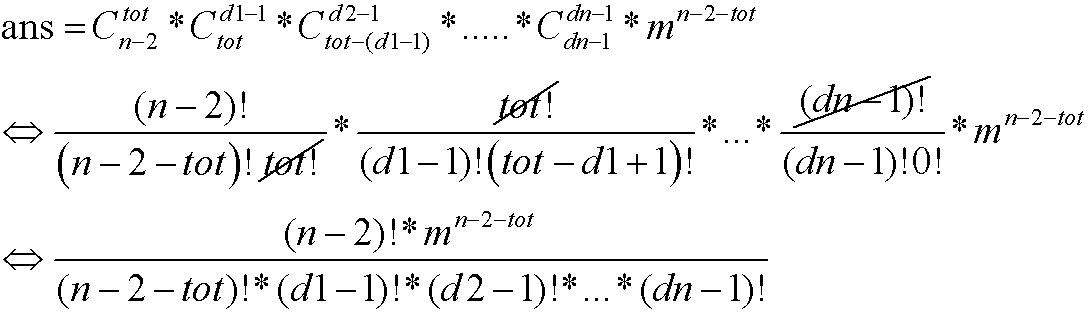
写到代码里，OK！

#include<stdio.h>
#include<stdlib.h>
#include<string>
#include<string.h>
#include<math.h>
#include<algorithm>
#include<iostream>
#include<set>
#include<vector>
#include<queue>
#include<map>
#define il inline
#define re register
using namespace std;
const int N=;
int n,m,p,d[N],ans[N],chk[N],pr[N],cnt[N],tot,l;
il void filt(){
    for(int i=;i<=;i++) if(!chk[i]){
        pr[++tot]=i;
        for(int j=i+i;j<=;j+=i)
            chk[j]=;
    }
}
il void add(int p,int v){
//    cout<<p<<"...\n";
    for(int k=;k<=p;k++){
        int x=k;
        for(int i=;i<=tot;i++){
            if(x<=) break;
            while(x%pr[i]==){
                cnt[i]+=v;x/=pr[i];
            }
        }
    }
}
il void mul(int x){
//    cout<<x<<endl;
    for(int i=;i<=l;i++)
        ans[i]*=x;
    for(int i=;i<=l;i++){
        ans[i+]+=ans[i]/;
        ans[i]%=;
    }
    while(ans[l+]>){
        l++;
        ans[l+]+=ans[l]/;
        ans[l]%=;
    }
}
int main(){
    filt();
    scanf("%d",&n);
    for(int i=;i<=n;i++){
        scanf("%d",&d[i]);
    }
    if(n==){
        if(!d[]) cout<<'';
        else cout<<'';
        return ;
    }
    for(int i=;i<=n;i++){
        if(!d[i]){
            printf("");
            return ;
        }
        if(d[i]==-) m++;
        else{
            d[i]--;p+=d[i];
        }
    }
    if(p>n-){
        printf("");
        return ;
    }
    add(n-,);
    add(n--p,-);
    for(int i=;i<=n;i++)
        if(d[i]>) add(d[i],-);
    ans[]=;l=;
/*    for(int i=1;i<=tot;i++)
        cout<<cnt[i]<<' ';
    cout<<endl;*/
    for(int i=;i<=tot;i++){
        for(;cnt[i];cnt[i]--)
            mul(pr[i]);
    }
//    cout<<m<<endl;
    for(int i=;i<=n--p;i++)
        mul(m);
    printf("%d",ans[l]);
    for(int i=l-;i>=;i--)
        printf("%06d",ans[i]);
    return ;
}

【bzoj1430】

Description

一开始森林里面有N只互不相识的小猴子，它们经常打架，但打架的双方都必须不是好朋友。每次打完架后，打架的双方以及它们的好朋友就会互相认识，成为好朋友。经过N-1次打架之后，整个森林的小猴都会成为好朋友。 现在的问题是，总共有多少种不同的打架过程。 比如当N=3时，就有{1-2,1-3}{1-2,2-3}{1-3,1-2}{1-3,2-3}{2-3,1-2}{2-3,1-3}六种不同的打架过程。

Input

一个整数N。

Output

一行，方案数mod 9999991。

Sample Input

4

Sample Output

96

HINT

50%的数据N<=10^3。
100%的数据N<=10^6。

【soltuion】

这不是刚刚那题的弱弱弱化版？

#include<stdio.h>
#include<stdlib.h>
#include<string>
#include<string.h>
#include<math.h>
#include<algorithm>
#include<iostream>
#include<set>
#include<vector>
#include<queue>
#include<map>
#define il inline
#define re register
#define mod 9999991
using namespace std;
typedef long long ll;
int n,ans=;
int main(){
    scanf("%d",&n);
    for(int i=;i<=n-;i++)
        ans=(ll)ans*n%mod;
    for(int i=;i<n;i++)
        ans=(ll)ans*i%mod;
    cout<<ans;
    return ;
}

我不会告诉你这篇博客只是一个刷题记录