fibonacci 数列及其应用

fibonacci 数列及其延展

fibonacci计算

fibonacci数列是指 0，1，1，2，3，5，8，13，21……这样自然数序列，即从第3项开始满足f(n)=f(n-1)+f(n-2)；

递归实现非常简单：

long long fibonacci(unsigned int n)
{
    int result[] = {, };

    if (n < )
        return result[n];

    return fibonacci(n-) + fibonacci(n-);
}

以计算f(10)为例，必须先求得f(9)和f(8)，要计算f(9)，又必须先求得f(8)和f(7)，如下图，可以发现存在大量重复的计算

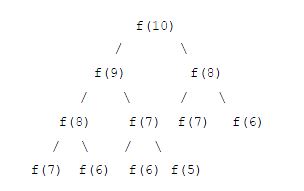
可见，当n比较大时，递归的算法效率非常低，比如计算f(100)机器就已经慢的不能接受了，用非递归的方法可以保证每个f(k)只被计算一次

long long fibonacci2(unsigned int n)
{
    int result[] = {, };

    if (n < )
        return result[n];

    unsigned k;
    long long m = ;
    long long prev = ;
    long long prev_prev = ;

    for (k=; k<=n; k++) {
        m = prev + prev_prev;
        prev_prev = prev;
        prev = m;
    }

    return m;
}

非递归的时间复杂度是O(n)。

下面介绍一种使用矩阵运算的方法，推导过程如下：

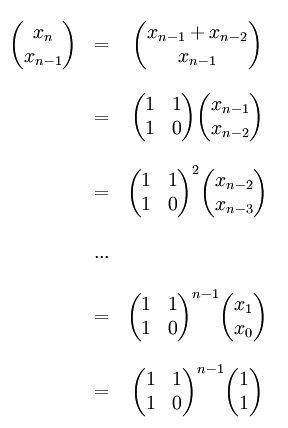
下面采用二分法计算矩阵的幂，时间复杂度只要O(logn)：

void multiply(int c[][], int a[][], int b[][])
{
    int tmp[][];

    tmp[][] = a[][]*b[][] + a[][]*b[][];
    tmp[][] = a[][]*b[][] + a[][]*b[][];
    tmp[][] = a[][]*b[][] + a[][]*b[][];
    tmp[][] = a[][]*b[][] + a[][]*b[][];

    c[][] = tmp[][];
    c[][] = tmp[][];
    c[][] = tmp[][];
    c[][] = tmp[][];
}

//二分法求矩阵幂
void matrix_pow(int a[][], int n)
{
    int unit[][];
    memcpy(unit, a, sizeof(unit));

    if (n < ) {

    } else if (n %  == ) {
        multiply(a, a, a);
        matrix_pow(a, n/);

    } else {
        multiply(a, a, a);
        matrix_pow(a, (n-)/);
        multiply(a, a, unit);
    }
}

long long fibonacci3(unsigned int n)
{
    int result[] = {, , }; 

    if (n < ) {
        return result[n];
    }   

    int matrix[][] = {{,},{,}};

    matrix_pow(matrix, n-);

    return matrix[][] + matrix[][];
}

实际上，fibonacci数列有通项公式，可以直接计算第n项的值：

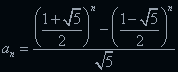
公式的具体推导过程参考这里。

---

fibonacci应用

在fibonacci数列中，当n趋向于无穷大时，前一项与后一项的比值越来越逼近黄金分割0.618，例如：

1÷1=1，1÷2=0.5，2÷3=0.666...，3÷5=0.6，5÷8=0.625，…………，55÷89=0.617977…，…………144÷233=0.618025…46368÷75025=0.6180339886…...

fibonacci质数的几个结论：

• f(3)=2和f(4)=3是Fibonacci质数；
• 从f(5)=5开始，某项为Fibonacci质数当且仅当它的项数为质数；
• 第k小的Fibonacci质数是以质数数列中的第k个数为项数的Fibonacci数（f(3)和f(4)除外）；

推导过程可以看这里。

对一个fibonacci数列 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89……，

而一个质数序列是2, 3, 5, 7, 11, 13, 17, 19……，以这个质数序列作为项数，对应的fibonacci项为：

f(5)=5，f(7)=13，f(11)=89，这些也都是质数。

如何判断一个整数是不是在fibonacci序列中

最简单的做法是依次计算 f(1)、f(2)……、f(n)，然后跟该整数比较看是否相等。

但当该整数非常大时，这种做法效率很低，一种更简单的方法参考这里，即一个数 N 如果满足 5 N^2 + 4 或 5N^2 – 4 能够开平方，则该数是fibonacci数。

 一个台阶总共有n级，如果一次可以跳1级，也可以跳2级。求总共有多少总跳法，并分析算法的时间复杂度。

首先我们考虑最简单的情况。如果只有1级台阶，那显然只有一种跳法。如果有2级台阶，那就有两种跳的方法了：一种是分两次跳，每次跳1级；另外一种就是一次跳2级。

现在我们再来讨论一般情况。我们把n级台阶时的跳法看成是n的函数，记为f(n)。当n>2时，第一次跳的时候就有两种不同的选择：一是第一次只跳1级，此时跳法数目等于后面剩下的n-1级台阶的跳法数目，即为f(n-1)；另外一种选择是第一次跳2级，此时跳法数目等于后面剩下的n-2级台阶的跳法数目，即为f(n-2)。因此n级台阶时的不同跳法的总数f(n)=f(n-1)+(f-2)。

我们把上面的分析用一个公式总结如下：

/  1 n=1
f(n) =     2 n=2
          \  f(n-1)+(f-2) n>2

这就是我们熟悉的Fibonacci序列。

对上面的题目再改进一下：

一个台阶总共有n级，如果一次可以跳1级，也可以跳2级......它也可以跳上n级。此时该青蛙跳上一个n级的台阶总共有多少种跳法？

用Fib(n)表示青蛙跳上n阶台阶的跳法数，设定Fib(0) = 1，

当n = 1 时，只有一种跳法，即1阶跳：Fib(1) = 1;
当n = 2 时，有两种跳的方式，一阶跳和二阶跳：Fib(2) = Fib(1) + Fib(0) = 2;
当n = 3 时，有三种跳的方式，第一次跳出一阶后，后面还有Fib(3-1)中跳法；第一次跳出二阶后，后面还有Fib(3-2)中跳法；第一次跳出三阶后，后面还有Fib(3-3)中跳法，即Fib(3) = Fib(2) + Fib(1)+Fib(0)=4;
当n = n 时，共有n种跳的方式，第一次跳出一阶后，后面还有Fib(n-1)中跳法； 第一次跳出二阶后，后面还有Fib(n-2)中跳法..........................第一次跳出n阶后，后面还有 Fib(n-n)中跳法，得到

Fib(n) = Fib(n-1)+Fib(n-2)+Fib(n-3)+..........+Fib(n-n) = Fib(0)+Fib(1)+Fib(2)+.......+Fib(n-1)

那么有

Fib(n-1) =  Fib(0)+Fib(1)+Fib(2)+.......+Fib(n-2)

两式相减，得到 Fib(n) - Fib(n-1) = Fib(n-1)，即 Fib(n) = 2*Fib(n-1)

现有长为144cm的铁丝，要截成n小段(n>2)，每段的长度不小于1cm,如果其中任意三小段都不能拼成三角形，则n的最大值为多少？

由于形成三角形的充要条件是任何两边之和大于第三边，因此不构成三角形的条件就是任意两边之和不超过最大边。截成的铁丝最小为1，因此可以放2个1，第三条线段就是2(为了使得n最大，因此要使剩下来的铁丝尽可能长，因此每一条线段总是前面的相邻2段之和)，依次为：1、1、2、3、5、8、13、21、34、55，以上各数之和为143，与144相差1，因此可以取最后一段为56，这时n达到最大为10。

 

用2X1（2行1列）的小矩形横着或者竖着去覆盖更大的矩形。请问用8个2X1的小矩形无重复地覆盖一个2X8的大矩形，总共有多少种方法。

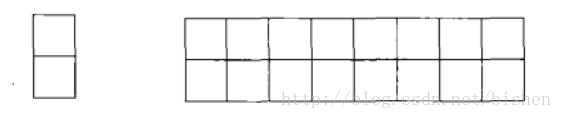
设f(8)表示覆盖2X8大矩形的方法综述。假设第一个小矩形是竖着去覆盖大矩形，那么还剩下由7个2X1的小矩形组成的大矩形f(7)；假设第一个小矩形是横着去覆盖大矩形，那么还剩下由6个2X1的小矩形组成的大矩形f(6)。即f(8)=f(7)+f(6)。依此类推，最后f(1)=1，f(2)=2。使用计算斐波那契数列的方法计算这道题目即可求出答案。

参考文档：

http://blog.csdn.net/hackbuteer1/article/details/6684867