[NOIP2014] 提高组 洛谷P2296 寻找道路

题目描述

在有向图G 中，每条边的长度均为1 ，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1 ．路径上的所有点的出边所指向的点都直接或间接与终点连通。

2 ．在满足条件1 的情况下使路径最短。

注意：图G 中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

输入输出格式

输入格式：

输入文件名为road .in。

第一行有两个用一个空格隔开的整数n 和m ，表示图有n 个点和m 条边。

接下来的m 行每行2 个整数x 、y ，之间用一个空格隔开，表示有一条边从点x 指向点y 。

最后一行有两个用一个空格隔开的整数s 、t ，表示起点为s ，终点为t 。

输出格式：

输出文件名为road .out 。

输出只有一行，包含一个整数，表示满足题目᧿述的最短路径的长度。如果这样的路径不存在，输出- 1 。

输入输出样例

输入样例#1：

3 2
1 2
2 1
1 3

输出样例#1：

-1

输入样例#2：

6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5

输出样例#2：

3

说明

解释1：

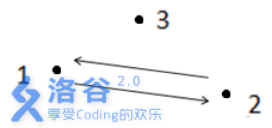
如上图所示，箭头表示有向道路，圆点表示城市。起点1 与终点3 不连通，所以满足题

目᧿述的路径不存在，故输出- 1 。

解释2：

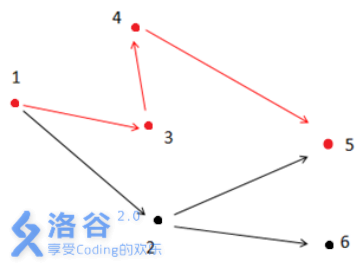
如上图所示，满足条件的路径为1 - >3- >4- >5。注意点2 不能在答案路径中，因为点2连了一条边到点6 ，而点6 不与终点5 连通。

对于30%的数据，0<n≤10，0<m≤20；

对于60%的数据，0<n≤100，0<m≤2000；

对于100%的数据，0<n≤10,000，0<m≤200,000，0<x，y，s，t≤n，x≠t。

先从终点开始BFS一遍，标记所有终点可以到达的点。

再从起点BFS一遍，要求与所经过的点相连的点必须是被标记过的。←然后就得到答案了

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 using namespace std;
 //
 int head[];
 int ct=,s,t;
 int used[],dis[];
 int n,m,x[],y[];
 //
 //邻接表处理
 struct edge{
     int next;
     int to;
 }e[];
 void add(int from,int to){
     e[++ct].to=to;
     e[ct].next=head[from];
     head[from]=ct;
     return;
 }
 bool pd(int pos){
     int i;
     for(i=head[pos];i;i=e[i].next){
         if(!used[e[i].to])return ;//未与终点联通
     }
     return ;
 }
 //
 int q[];
 int main(){
     scanf("%d%d",&n,&m);
     int i,j;
     for(i=;i<=m;i++){
         scanf("%d%d",&x[i],&y[i]);
         add(y[i],x[i]);//第一遍反向制表
     }
     scanf("%d%d",&s,&t);
     //bfs
     int hd=,tl=;
     q[]=t;
     used[t]=;
     while(hd<=tl){
         int pos=q[hd];
         hd++;
         for(i=head[pos];i;i=e[i].next){
             if(!used[e[i].to]){
                 q[++tl]=e[i].to;
                 used[e[i].to]=;
             }
         }
     }
     //finish
     if(!used[s]){
         printf("-1");
         return ;
     }
     memset(head,,sizeof(head));
     memset(q,,sizeof(q));
     memset(dis,-,sizeof(dis));
     ct=;
     for(i=;i<=m;i++){
         add(x[i],y[i]);
     }
     //bfs
     q[]=s;
     dis[s]=;
     hd=;tl=;
     int ans=;
     while(hd<=tl){
         int pos=q[hd];
         hd++;
         if(pd(pos)==)continue;
         for(i=head[pos];i;i=e[i].next){
             if(dis[e[i].to]    ==-)
             {
                 dis[e[i].to]=dis[pos]+;
                 q[tl++]=e[i].to;
                 if(e[i].to==t){
                     ans=dis[t];
                     printf("%d",ans);
                     return ;
                 }
             }
         }
     }
     //finish
     printf("-1");
     return ;
 }