AHOI2005航线规划 bzoj1969（LCT缩点）

题目描述

对Samuel星球的探险已经取得了非常巨大的成就，于是科学家们将目光投向了Samuel星球所在的星系——一个巨大的由千百万星球构成的Samuel星系。

星际空间站的Samuel II巨型计算机经过长期探测，已经锁定了Samuel星系中许多星球的空间坐标，并对这些星球从1开始编号1、2、3……。

一些先遣飞船已经出发，在星球之间开辟探险航线。

探险航线是双向的，例如从1号星球到3号星球开辟探险航线，那么从3号星球到1号星球也可以使用这条航线。

例如下图所示：

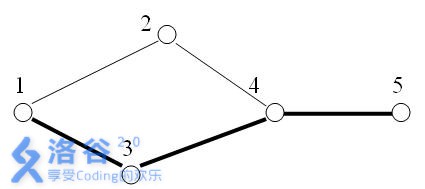
在5个星球之间，有5条探险航线。

A、B两星球之间，如果某条航线不存在，就无法从A星球抵达B星球，我们则称这条航线为关键航线。

显然上图中，1号与5号星球之间的关键航线有1条：即为4-5航线。

然而，在宇宙中一些未知的磁暴和行星的冲撞，使得已有的某些航线被破坏，随着越来越多的航线被破坏，探险飞船又不能及时回复这些航线，可见两个星球之间的关键航线会越来越多。

假设在上图中，航线4-2（从4号星球到2号星球）被破坏。此时，1号与5号星球之间的关键航线就有3条：1-3，3-4，4-5。

小联的任务是，不断关注航线被破坏的情况，并随时给出两个星球之间的关键航线数目。现在请你帮助完成。

输入输出格式

输入格式：

第一行有两个整数N，M。表示有N个星球（1< N < 30000），初始时已经有M条航线（1 < M < 100000）。随后有M行，每行有两个不相同的整数A、B表示在星球A与B之间存在一条航线。接下来每行有三个整数C、A、B。C为1表示询问当前星球A和星球B之间有多少条关键航线；C为0表示在星球A和星球B之间的航线被破坏，当后面再遇到C为1的情况时，表示询问航线被破坏后，关键路径的情况，且航线破坏后不可恢复； C为-1表示输入文件结束，这时该行没有A,B的值。被破坏的航线数目与询问的次数总和不超过40000。

输出格式：

对每个C为1的询问，输出一行一个整数表示关键航线数目。

输入输出样例

输入样例#1：复制

输出样例#1：复制

1

3

说明

我们保证无论航线如何被破坏，任意时刻任意两个星球都能够相互到达。在整个数据中，任意两个星球之间最多只可能存在一条直接的航线。

题解

LCT维护双联通分量

然而蒟蒻完全不知道怎么实现orz，于是只好（恬不知耻地）看着题解学了一个晚上

首先肯定是要将所有操作读入倒叙做的

还有，答案就是缩完点后两点间的路径长

最重要的问题是怎么连边

如果本来不相连，直接连

已经在同一个双连通分量，忽略

否则的话，用并查集维护在哪一个双连通，直接暴力将所有缩到一起就是了

可以发现每缩一次点就减少一个，所以最多缩$n$次

还有一个细节，我好久才搞明白，写在代码里了

 //minamoto

 #include<bits/stdc++.h>

 using namespace std;

 #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)

 char buf[<<],*p1=buf,*p2=buf;

 inline int read(){

     #define num ch-'0'

     char ch;bool flag=;int res;

     while(!isdigit(ch=getc()))

     (ch=='-')&&(flag=true);

     for(res=num;isdigit(ch=getc());res=res*+num);

     (flag)&&(res=-res);

     #undef num

     return res;

 }

 char obuf[<<],*o=obuf;

 inline void print(int x){

     if(x>) print(x/);

     *o++=x%+;

 }

 const int N=,M=;

 struct edge{

     int x,y;

     inline bool operator <(const edge&b)const

     {return x<b.x||(x==b.x&&y<b.y);}

 }e[M];

 int fa[N],f[N],sz[N],s[N],ch[N][],rev[N],vis[N],top;

 int ff(int x){return f[x]==x?x:f[x]=ff(f[x]);}

 inline bool isroot(int x){return ch[fa[x]][]!=x&&ch[fa[x]][]!=x;}

 inline void pushup(int x){sz[x]=sz[ch[x][]]+sz[ch[x][]]+;}

 inline void pushdown(int x){

     if(x&&rev[x]){

         swap(ch[x][],ch[x][]);

         rev[ch[x][]]^=,rev[ch[x][]]^=,rev[x]=;

     }

 }

 void rotate(int x){

     int y=fa[x],z=fa[y],d=ch[y][]==x;

     if(!isroot(y)) ch[z][ch[z][]==y]=x;

     fa[x]=z,fa[y]=x,fa[ch[x][d^]]=y,ch[y][d]=ch[x][d^],ch[x][d^]=y;pushup(y);

 }

 void splay(int x){

     s[top=]=x;for(int i=x;!isroot(i);i=fa[i]) s[++top]=fa[i];

     for(int i=top;i;--i) pushdown(s[i]);

     for(int y=fa[x],z=fa[y];!isroot(x);y=fa[x],z=fa[y]){

         if(!isroot(y)) ((ch[y][]==x)^(ch[z][]==y))?rotate(x):rotate(y);

         rotate(x);

     }

     pushup(x);

 }

 void access(int x){

     for(int y=;x;y=x,x=fa[x]=ff(fa[x]))

     splay(x),ch[x][]=y,pushup(x);

 }

 inline void makeroot(int x){

     access(x),splay(x),rev[x]^=;

 }

 int findroot(int x){

     access(x),splay(x);

     pushdown(x);

     while(ch[x][]) pushdown(x=ch[x][]);

     splay(x);

     return x;

 }

 inline void split(int x,int y){

     makeroot(x),access(y),splay(y);

 }

 void del(int x,int y){

     if(x) f[x]=y,del(ch[x][],y),del(ch[x][],y);

 }

 void merge(int x,int y){

     if(x==y) return;

     makeroot(x);

     if(findroot(y)!=x) return(void)(fa[x]=y);

     /*makeroot的时候打了标记

     所以findroot的时候顺便把标记放掉

     再把根转到splay的根节点

     然后因为x为根，y深度必然大于x

     所以把所有右节点搞掉就好了

     */

     del(ch[x][],x);

     ch[x][]=,pushup(x);

 }

 int op[N],ans[M],a[M],b[M];

 int main(){

     //freopen("testdata.in","r",stdin);

     int n,m,i,j;

     n=read(),m=read();

     for(i=;i<=n;++i) sz[i]=,f[i]=i;

     for(i=;i<=m;++i){

         int u=read(),v=read();

         if(u>v) swap(u,v);

         e[i]=(edge){u,v};

     }

     sort(e+,e++m);

     for(j=;op[j]=read(),op[j]!=-;++j){

         int u=read(),v=read();

         if(!op[j]){

             if(u>v) swap(u,v);

             vis[lower_bound(e+,e++m,(edge){u,v})-e]=;

         }

         a[j]=u,b[j]=v;

     }

     for(i=;i<=m;++i)

     if(!vis[i]) merge(ff(e[i].x),ff(e[i].y));

     for(i=,--j;j;--j){

         int u=ff(a[j]),v=ff(b[j]);

         if(op[j]) split(u,v),ans[++i]=sz[v]-;

         else merge(u,v);

     }

     while(i) print(ans[i--]),*o++='\n';

     fwrite(obuf,o-obuf,,stdout);

     return ;

 }