NOI2013 Day1

NOI2013 Day1

向量内积

题目描述：两个\(d\)维向量\(A\)与\(B\)的内积为其相对应维度的权值的乘积和，现有\(n\)个\(d\)维向量 ，求是否存在两个向量的内积为\(k\)(\(k=2,3\))的倍数。

solution:

考虑\(k=2\)，以下为在\((mod 2)\)下运算，设矩阵\(A_1,A_2\),

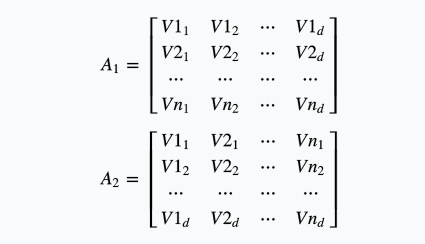
设矩阵\(P=A_1 * A_2\)，若非对角线出现\(0\)，则有一对内积为\(0\)

\(P\)对角线上的\(0\)要处理一下

设矩阵\(F\)，令\(F_{ii}+P_{ii}=1\),其余为\(0\)

设矩阵\(G\)全为\(1\)

矩阵\(T=G-F-P\)，问题转为求是否有一元素在\(T\)中为\(1\)

随机一\(n * 1\)矩阵\(X\)，若\(L=T * X,L_{i,1}=1\),则\(T_i\)有一元素为\(1\)

\(L=T * X=G * X-F * X-A_1 * (A_2 * X)\)

第一部分\(O(n)\), 第二部分\(O(nd)\)，第三部分\(O(nd)\)。

考虑\(k=3\)，\((mod 3)=0,1,2\)，因为\(1 * 1=1(mod 3),2 * 2=1(mod 3)\),所以将内积结果平方就可以了。

假设两个\(d\)维向量\(A,B\)

\((A * B)^2=(A_1B_1+A_2B_2+ \cdots +A_dB_d)(A_1B_1+A_2B_2+ \cdots +A_dB_d)\)

\(=(A_1A_1+A_1A_2+ \cdots +A_1A_d+A_2A_1+ \cdots +A_2A_d+ \cdots +A_dA_d)*(B_1B_1+B_1B_2+ \cdots +B_1B_d+B_2B_1+ \cdots +B_2B_d+ \cdots +B_dB_d)\)

所以只需要将\(d\)维扩展到\(d^2\)维即可， 以上操作均在\((mod 3)\)下运算，所以只要\(L\)有非零就可以了。

时间复杂度：\(O(nd^2)\)

东方非想天则Orz

树的计数

题目描述：给定一个 DFS 序和 BFS 序，求符合条件的有根树中，树的高度的平均值。

solution：

这题有点求期望值的味道。

根据\(BFS\)序对\(DFS\)序重标号。\(pos[i]\)表示\(i\)在\(DFS\)的第几位,\(deep[i]\)为\(i\)的深度

for (int i=1; i<=n; ++i) w[BFS[i]]=i;
for (int i=1; i<=n; ++i) DFS[i]=w[DFS[i]];
for (int i=1; i<=n; ++i) pos[DFS[i]]=i;

约束条件：

1、\(1\)为根

2、对于\(BFS\)连续的一段\([L, R]\)，如果它们在同一层，必有\(pos[L]<pos[L+1]<\cdots<pos[R]\)

3、对于\(DFS\)的相邻两个数\(d[i],d[i+1]\),必有\(deep[d[i+1]]\leq deep[d[i]]+1\)

设\(s[i]\)，当\(s[i]=1\)时，\(i\)与\(i+1\)不在同一层，当\(s[i]=0\)时，可能在同一行也可能不在。

转化约束条件：

1、\(s[i]=1\)

2、若\(pos[i+1]<pos[i],s[i]=1\)

3、若\(DFS[i]<DFS[i+1]\)，则\(\sum_{j=d[i]}^{d[i+1]-1} s[i]\leq1\)（若\(DFS[i]>DFS[i+1]\),从\(BFS\)得\(deep[d[i+1]]\leq deep[d[i]]\)）

用打标记的方法来表示某一段的\(s[i]\)的值是否确定，不确定的\(s[i]\)可以取\(0,1\)对答案的贡献为\(0.5\)。

因为\(i+1\)可以是\(i\)的儿子或兄弟要满足一下条件：

1、\(i+1\)为儿子时，\(i\)为所在层的最后一个，当\(i+1\)做兄弟时，\(i+1\)为所在层最后一个

2、其它不在\(i\)子树或\(i+1\)子树的点的深度均不超过\(i\)，否则\(BFS\)有误。

以\(i+1\)为根的子树方案数是一定的，做儿子还是做兄弟只是多\(1\)的影响，所以贡献为\(0.5\)

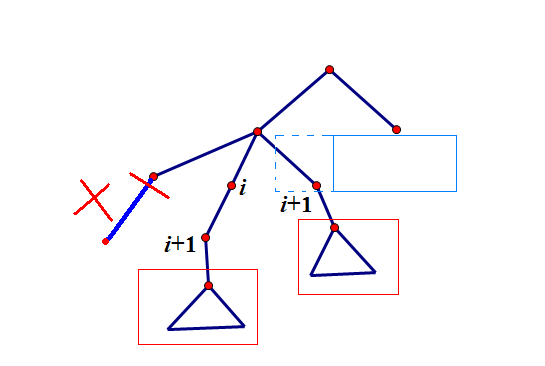
（蓝框内不能有点，红框方案相同，最左边错误）

#include <cstdio>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <ctime>
#include <algorithm>
#include <deque>
#include <queue>
#include <vector>
#include <map>
#include <complex>
using namespace std;

const int maxn=int(2e5)+100;
typedef int arr[maxn];

int n;
arr DFS, BFS, w, x, mat, sum, pos;
double ans;

void init()
{
	scanf("%d", &n);
	for (int i=1; i<=n; ++i) scanf("%d", &DFS[i]);
	for (int i=1; i<=n; ++i) scanf("%d", &BFS[i]);
	for (int i=1; i<=n; ++i) w[BFS[i]]=i;
	for (int i=1; i<=n; ++i) DFS[i]=w[DFS[i]];
	for (int i=1; i<=n; ++i) pos[DFS[i]]=i;
}
void solve()
{
	x[1]=1;
	//mat用来标记那一段是确定的
	mat[1]++; mat[2]--;
	for (int i=1; i<n; ++i)
		if (pos[i]>pos[i+1])
		{
			x[i]=1;
			mat[i]++; mat[i+1]--;
		}
	for (int i=1; i<=n; ++i) sum[i]=sum[i-1]+x[i];
	for (int i=1; i<n; ++i)
		if (DFS[i]<DFS[i+1])
		{
			if (sum[DFS[i+1]-1]-sum[DFS[i]-1])
			{
				mat[DFS[i]]++;
				mat[DFS[i+1]]--;
			}
		}
	for (int i=1, cnt=0; i<n; ++i)
	{
		cnt+=mat[i];
		if (cnt) ans+=x[i];//cnt>0说明s[i]是确定的
		else ans+=0.5;
	}
}
int main()
{
	freopen("count.in", "r", stdin);
	freopen("count.out", "w", stdout);
	init();
	solve();
	printf("%.3lf\n", ans+1.0);
	return 0;
}

时间复杂度：\(O(n)\)