[学习笔记] CS131 Computer Vision: Foundations and Applications：Lecture 3 线性代数初步

向量和矩阵

什么是矩阵/向量？

Vectors and matrix are just collections of ordered numbers that represent something: movements in space, scaling factors, pixel brightness, etc. We'll define some common uses and standard operations on them.

向量：列向量/行向量

用处：

• Vectos can represented an offset in 2D or 3D space; points are just vectors from the origion
• data(pixels, gradient at an image key point)can be treated as a vector

矩阵：在python中图像被表示为像素亮度矩阵, grayscale(m*n), color(m*n*3)

算术运算：

• addition
• scaling
• norm: vector/matrix

• inner prodcut/dot product of vectors
• product of matrix
• transpose
• determinant

通常任何满足以下四种性质的函数都可以作为范数：

• 非负性
• 正定性
• 齐次性
• 三角不等式

特殊矩阵

• 单位阵
• 对角阵
• 对称阵
• 反对阵矩阵

变换矩阵

矩阵可以用来对向量进行变换

• scaling
• rotation

齐次系统/齐次坐标：

变换矩阵最右列被加到原有向量中

这里有时候会用到前面看的仿射矩阵affine matrix 的知识(见参考资料)：

平移(translation):

缩放(scaling)

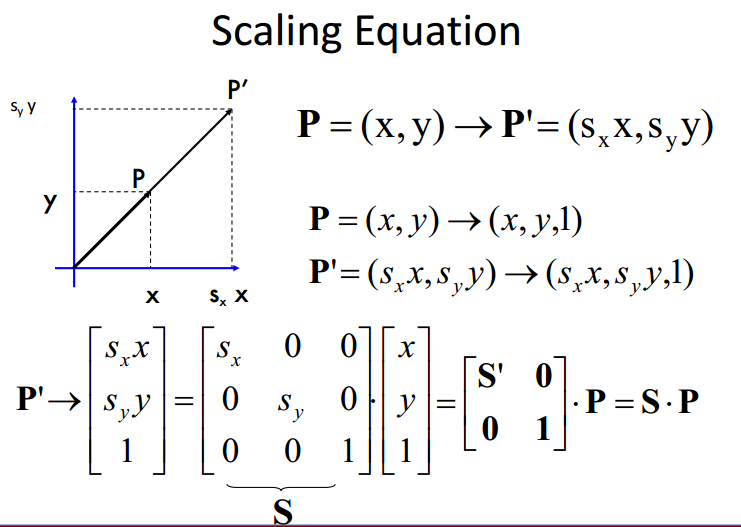
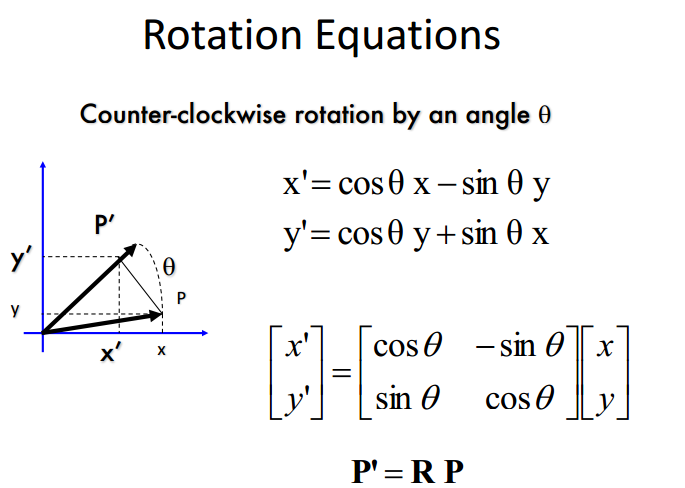
旋转(rotation)

平移旋转缩放

矩阵的逆

如果A的逆存在，A是可逆的或者是非奇异的non-singular; 否则是不可逆或者是奇异的.

伪逆(pseudoinverse):在计算大型矩阵逆的时候，会伴随这浮点数问题，而且不是每个矩阵都有逆

np.linalg(A,B) to solve AX = B

如果没有具体解, 返回最近的一个解

如果有多个解，返回最小的那个解

矩阵的阶

the rank of a transforamtion matrix tells you hwo many dimensions it transforms a vector to.

满秩; m*m 矩阵，阶数为m

阶数 < 5, 奇异矩阵，逆不存在

非方阵没有逆

特征值和特征向量

what is eigenvector?

An eigenvector x of a linear transformation A is a non-zero vector that when A is applied to it, does not change direction. And only scales the eigenvector by the scalar value \lambda, called an eigenvalue.

$$Ax = \lambda x$$

$Ax = (\lambda I)x,  \rightarrow (\lambda I - A)x = 0$, $x$ is non-zero, thus,  $|(\lambda I - A)| = 0$

性质：

• $tr(A) = \sum_{i=1}^n \lambda_i$
• $|A| = \prod_{i=1}^n \lambda_i$
• the rank of A is equal to the number of non-zero eigenvalues of A
• the eigenvalues of a diagonal matrix $D = diag(d_1,...d_n)$ are just the diagonal entries $d_1, ..., d_n$

分形理论(spectral theroy)

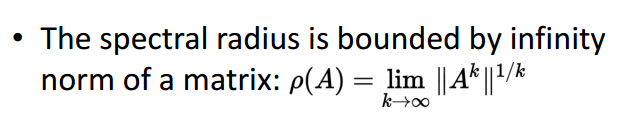
对角化(diagonalization)

如果n*n矩阵有n个线性独立的特征向量，则它是可对角化的

如果n*n矩阵有n个不同的特征值，则它是可对角化的

对应着不同特征值的特征向量是线性独立的

所有的特征向量方程可以写为：

$$AV = VD$$

$V \in R^{n*n}$  V的列是A的特征向量，D为对角矩阵，对应着值为A的特征值. 如果A可以写为：$A = VDV^{-1}$则A可对角化

特征值特征向量和对称对阵

对称矩阵的性质：$A^{-1} = A^T$, A所有的特征值都是实数，A所有的特征向量都是正交的.

Some applications of eigenvlues:  PageRank, Schrodinger's equation, PCA

矩阵代数

矩阵梯度：

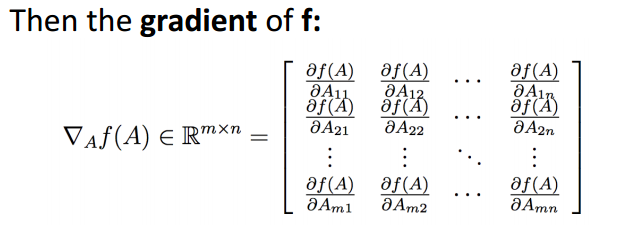
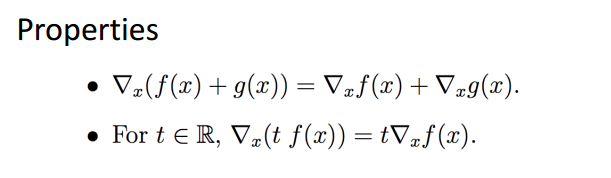
Hessian Matrix

参考资料：

https://docs.microsoft.com/en-us/dotnet/framework/winforms/advanced/how-to-rotate-reflect-and-skew-images