Codeforces Round #369 (Div. 2) D. Directed Roads —— DFS找环 + 快速幂

题目链接：http://codeforces.com/problemset/problem/711/D

D. Directed Roads

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

ZS the Coder and Chris the Baboon has explored Udayland for quite some time. They realize that it consists of n towns numbered from 1 to n.

There are n directed roads in the Udayland. i-th
of them goes from town i to some other town ai (ai ≠ i).
ZS the Coder can flip the direction of any road in Udayland, i.e. if it goes from town A to town B before
the flip, it will go from town B to town A after.

ZS the Coder considers the roads in the Udayland confusing, if there is a sequence of distinct towns A1, A2, ..., Ak (k > 1)
such that for every 1 ≤ i < k there is a road from town Ai to
town Ai + 1 and
another road from town Ak to
town A1.
In other words, the roads are confusing if some of them form a directed cycle of some towns.

Now ZS the Coder wonders how many sets of roads (there are 2n variants)
in initial configuration can he choose to flip such that after flipping each road in the set exactly once, the resulting network will not be confusing.

Note that it is allowed that after the flipping there are more than one directed road from some town and possibly some towns with no roads leading out of it, or multiple roads between any pair of cities.

Input

The first line of the input contains single integer n (2 ≤ n ≤ 2·105) —
the number of towns in Udayland.

The next line contains n integers a1, a2, ..., an (1 ≤ ai ≤ n, ai ≠ i), ai denotes
a road going from town i to town ai.

Output

Print a single integer — the number of ways to flip some set of the roads so that the resulting whole set of all roads is not confusing. Since this number may be too large, print the answer modulo 109 + 7.

Examples

input

3
2 3 1

output

6

input

4
2 1 1 1

output

8

input

5
2 4 2 5 3

output

28

Note

Consider the first sample case. There are 3 towns and 3 roads. The towns are numbered from 1 to 3 and the roads are , ,  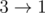initially. Number the roads 1 to 3 in this order.

The sets of roads that ZS the Coder can flip (to make them not confusing) are {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}. Note that the empty set is invalid because if no roads are flipped, then towns 1, 2, 3 is form a directed cycle, so it is confusing. Similarly, flipping all roads is confusing too. Thus, there are a total of 6 possible sets ZS the Coder can flip.

The sample image shows all possible ways of orienting the roads from the first sample such that the network is not confusing.

题解：

1.根据题意， n个点共有n条边。那么表明每个连通块中， 有且仅有一个环， 且这个环可能还有一些“线丝”挂在上面。

2.首先对于一个连通块而言， 可分为环部分和线丝部分：对于环部分，如果有k个点， 那么有(1<<k)-2种情况可以去环。（-2是减去所有都flip或者所有都不flip这两种情况，因为这两种情况都不能 去环）， 对于线丝部分， 他们的状态对环没有影响，假设线丝有t个点，那么状态数为1<<t。

最后将每个连通块的环部分和线丝部分的状态数相乘， 即为答案。

找环问题：

1.group[]数组记录当前点时是在哪一次的dfs中访问到的。vis[]记录当前点在这次dfs中是第几个被访问的元素。

2.在dfs的过程中， 当遇到被访问过的元素时： 如果它的group[i]为这次dfs所标记的， 那么表明这次dfs构成了环； 如果group[i]为之前dfs所标记的， 那么表明这次dfs出来的是线丝（遇到的连通块必定有环。因为：假设无环，那么就可以dfs出环了，说明假设不成立）。

代码如下：

 #include<bits/stdc++.h>
 #define ms(a, b)  memset((a), (b), sizeof(a))
 using namespace std;
 typedef long long LL;
 const double eps = 1e-;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int mod = 1e9+;
 const int maxn = 2e5+;

 int n, a[maxn];
 int vis[maxn], group[maxn];
 LL ans;

 LL qpow(LL x, LL y)
 {
     LL s = ;
     while(y)
     {
         if(y&) s = (s*x)%mod;
         x = (x*x)%mod;
         y >>= ;
     }
     return s;
 }

 void dfs(int k, int id, int cnt)  //dfs出环， 或者dfs出线丝
 {
     vis[k] = cnt;
     group[k] = id;

     if(vis[a[k]]) //遇到了被访问过的元素
     {
         if(group[a[k]]==id)  //dfs出环
         {
             ans *= qpow(,cnt-vis[a[k]]+)-, ans %= mod;  //环的部分
             ans *= qpow(, vis[a[k]]-), ans %= mod;  // 环之外的那条线
         }
         else ans *= qpow(,cnt), ans %= mod;  //dfs出线丝
     }
     else dfs(a[k], id, cnt+);
 }

 int main()
 {
     scanf("%d",&n);
     for(int i = ; i<=n; i++)
         scanf("%d",&a[i]);

     ans = ;
     ms(vis,);
     ms(group,);
     for(int i = ; i<=n; i++)
         if(!vis[i])
             dfs(i,i,);

     printf("%lld\n", ans);
 }