编程哲学之 C# 篇：007——如何创造万物

上帝拥有创建万物的能力，本文介绍创造万物的道，让你也拥有上帝般创造万物的能力！

道

中国哲学家，道家学派创始人——老子，在《道德经》写到：

道生一，一生二，二生三，三生万物

那么，是什么 道 可以创造万物？

古希腊的哲学家们曾做过这样的推理：
如果将水、沙子、肉无限切分，最后得到的将是相同的不可分的颗粒。
这些以不同的方式连接在一起的不可分的颗粒，希腊人称之为“原子”。

那么我们用同样的思维来推理，
如果将电脑世界中文字、图片、音乐、电影、游戏、无限切分，
最后能否得到的将是相同的不可分的东西？如果能？那么这个东西又是什么？

回忆一下初中的化学知识：
石墨、金刚石，它们都是由 C(碳) 原子构成的，但由于它们的 C(碳) 原子排列方式不同，从而造成了它们是不同的东西。

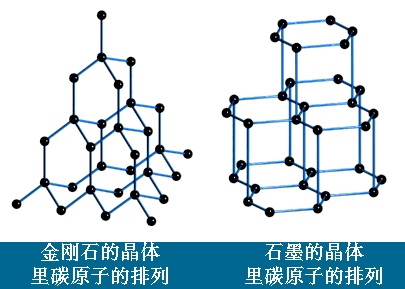
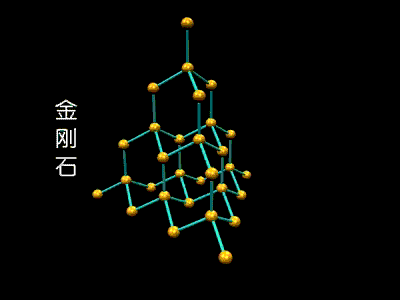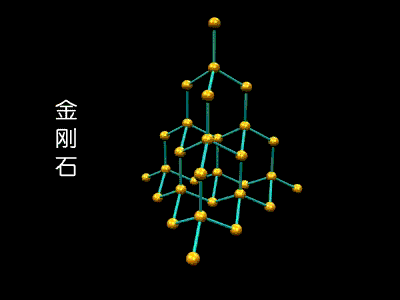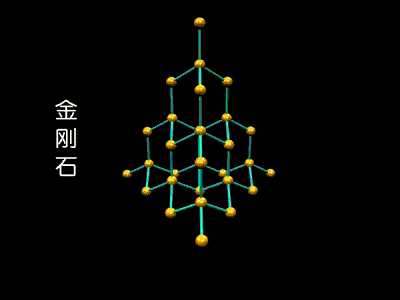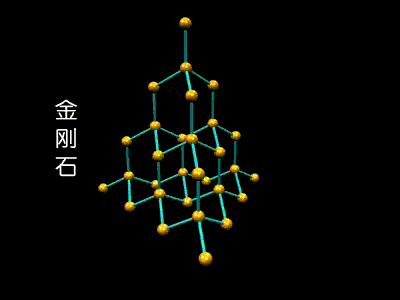
看来创造万物的 道 是：最小不可分割的颗粒 + 排列方式

现实世界中的难题：

• 物理学家们依然在寻找 最小不可分割的颗粒 的最终形态。
• 即使想要将 原子 按意愿组织起来是极其艰难的。

怎么解决上面说到的两个难题？

在现实世界中，
我们想要合成一种新的元素极其艰难的原因之一是，排列是以三维立体的形式来呈现的。
如果我们能将三维降到一维，那么一切将会简单很多，那么一维排序能否创造出万物呢？

让我们来看看 7000 多年前的伏羲——华夏文明的人文始祖，是怎么用他独特的方式来描述这个世界的。

7000 多年前，人类还没有发明文字，
伏羲看到世界：有天、有地；有男、有女；有光、有暗......
悟出了天地万物的变化规律惟一阴一阳而已。
所以根据阴阳变化之理，创造了八卦，以八种简单的符号来概括天地之间的万事万物。

符号	卦名	拼音	象征
☰	乾	qián	天
☱	兑	duì	泽
☲	离	lí	火
☳	震	zhèn	雷
☴	巽	xùn	风
☵	坎	kǎn	水
☶	艮	gèn	山
☷	坤	kūn	地

可以看出，只要用三个位，每个位置上要么是阳，要么是阴，就可以代表成八种不同的事物。
记作：2^3 = 2³ = 8

接下来看看由八卦扩展到六十四卦

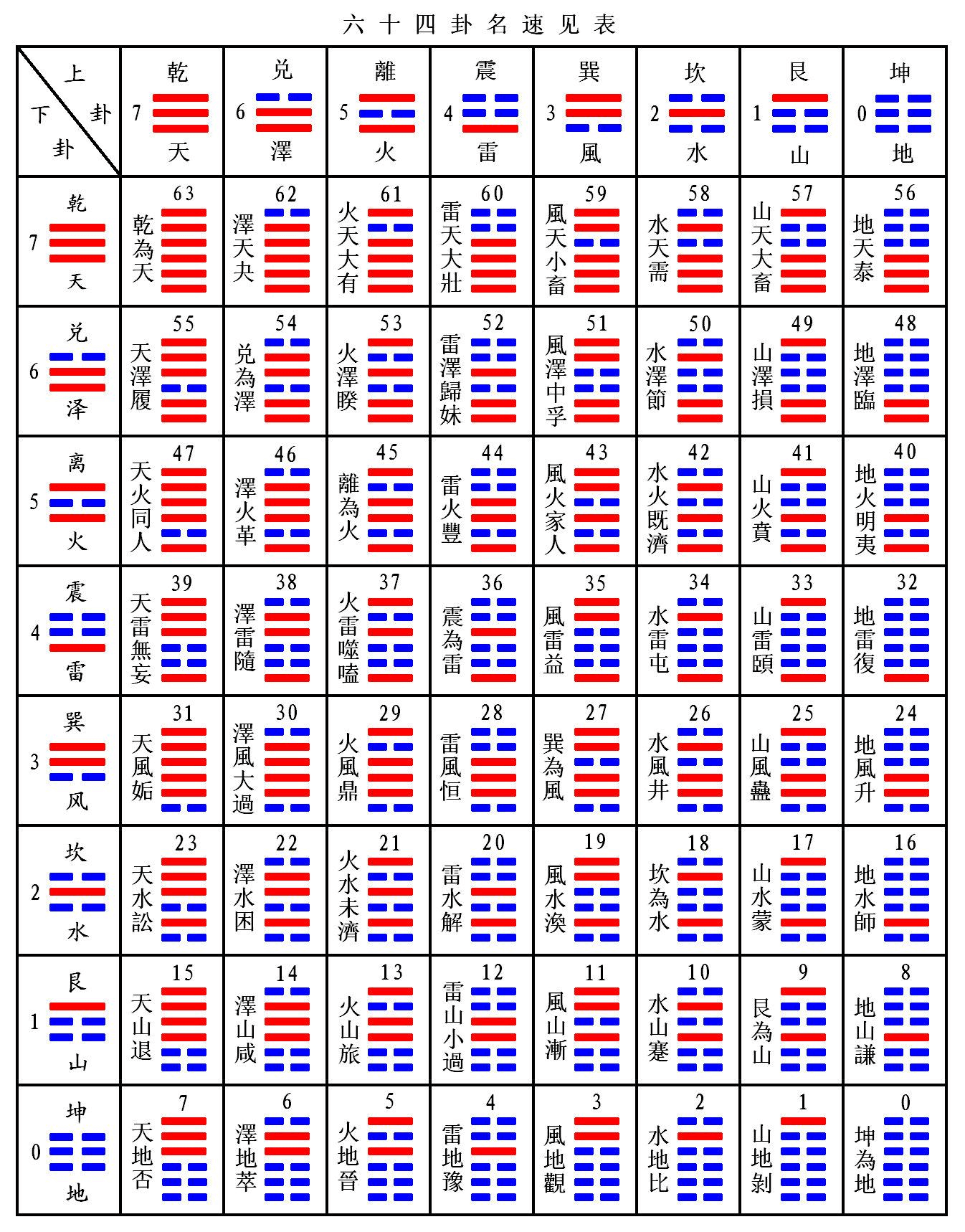
可以看出，只要用六个位，每个位置上要么是阳，要么是阴，就可以代表成六十四种不同的事物。
以此类推，只要我们不断地增加更多的位，就可以表示更多的事物，
用极限的思想来诉说。就可以表示用来表示万事万物。

我们运用古希腊哲学家的推理来无限切割六十四卦中的任何一个卦象，
也就是对半切，再对半切，再对半切...
直到最后，我们得到 最小不可分割的阳 或 最小不可分割的阴
貌似有两种 最小不可分割的颗粒

如果是只有一种 最小不可分割的颗粒 就好了。
再看看我们的 金刚石 和 石墨 的结构图吧。

在 金刚石 和 石墨 的结构图，
有原子的点，我们称之为有，
没有原子的空白空间也有最小不可分割空间(刚好可以容下一个原子，但还没有)，我们称之为无

所以，最小不可分割空间上要么有最小不可分割的颗粒，要么没有(无)，只有这两种可能。
替换一下八卦中的阴阳：
阳 = 有
阴 = 无 (因为 阴 = 无了，所以我们只剩下 阳 了)

也可以：
阳 = 无
阴 = 有 (因为 阳 = 无了，所以我们只剩下 阴 了)

用更简单的符号来表示吧：
阳 = 有 = 1
阴 = 无 = 0

想象一下，将金刚石 和 石墨 的结构图中
有原子点用 1 代替，
空白空间用 0 代替(不是整片空白，而是刚好可以容下一个原子最小不可分割空白空间)

所以我们得到了 最小不可分割的颗粒 —— 1，
而 0 则表示 最小不可分割空白空间，也可以来容下 最小不可分割的颗粒 —— 1，但目的是为了隔开 1，让其呈现排列结构

符号	卦名	拼音	象征	新表示方式
☰	乾	qián	天	111
☱	兑	duì	泽	011
☲	离	lí	火	101
☳	震	zhèn	雷	001
☴	巽	xùn	风	110
☵	坎	kǎn	水	010
☶	艮	gèn	山	100
☷	坤	kūn	地	000

前面说了，创造万物的 道 是：最小不可分割的颗粒 + 排列方式

所以，在我们创造的世界中，由于我们是神，
因此我们可以指定 最小不可分割的颗粒 是 1，
然后用 一维排列的排列方式，就可以在我们创造的世界中创造万物！

在数字网络时代，你看到的文字、图片、音乐、电影、游戏，这一切都是由 1 和 0 组成。

二进制的发明者莱布尼兹首次接触到八卦图是与 1685年 来中国作为传教士白晋的联系中。

佛

在现实世界中，物理结构相同则是同样的事物，物理结构不同则是不同的事物。
然后佛且告诉我们，一切由心而生。

看山是山，看山不是山，看山还是山~

在现在的电脑世界中，同样的排列方式可以表示多种事物，取决于你怎么“看”，
如：
01100001 = 可以表示：字母 a
01100001 = 可以表示：数字 97

如果我们将其相加，可能有多种结果：
01100001 + 01100001 = aa
01100001 + 01100001 = a97
01100001 + 01100001 = 97a
01100001 + 01100001 = 194

一切的因果取决你心中的“看”法

在数字网络中，一切的交流都是由 1 和 0 组成。
如果一台电脑将 01100001 发送给另外另外一台电脑，
另外一台电脑是否能明白取决于两个电脑是否拥有相同的“看”法。

所以，戒酒戒色，练武功都不会让你成佛，
你是否能成佛，取决于你对这个世界的“看”法是否和佛的“看”法一样。

这里有点讲得有点玄了，下几章讲到编程中得类型应该就会好懂很多了。

太极

八卦图是由伏羲画的，中间的太极图是由孔子画的。
太 由 大 和 点 组成，在孔子的哲学观中：
这个世界是由 大到极限(宇宙) 和 (点)小到极限(最小不可分割的颗粒) 的组成的。

下一章，我们将开始用 小到极限(最小不可分割的颗粒) 在 大到极限(宇宙) 中创建万物！

结束语

在很多计算机书籍中都会有下面一段话：

比特(bit)是英文 binary digit 的缩写，表示信息的最小单位，只有两种元素：0 和 1 。

本章的内容就是解释为什么只用 0 和 1 就能来描述我们现实世界中的一切。

最后说明：本章内容和思想是计算机与信息时代的根基，适合任意编程语言。