「NOIP2016」「P1850」换教室（期望dp

题目描述

对于刚上大学的牛牛来说，他面临的第一个问题是如何根据实际情况申请合适的课程。

在可以选择的课程中，有 2n2n 节课程安排在 nn 个时间段上。在第 ii（1 \leq i \leq n1≤i≤n）个时间段上，两节内容相同的课程同时在不同的地点进行，其中，牛牛预先被安排在教室 c_ici 上课，而另一节课程在教室 d_idi 进行。

在不提交任何申请的情况下，学生们需要按时间段的顺序依次完成所有的 nn 节安排好的课程。如果学生想更换第 ii节课程的教室，则需要提出申请。若申请通过，学生就可以在第 ii 个时间段去教室 d_idi 上课，否则仍然在教室 c_ici 上课。

由于更换教室的需求太多，申请不一定能获得通过。通过计算，牛牛发现申请更换第 ii 节课程的教室时，申请被通过的概率是一个已知的实数 k_iki，并且对于不同课程的申请，被通过的概率是互相独立的。

学校规定，所有的申请只能在学期开始前一次性提交，并且每个人只能选择至多 mm 节课程进行申请。这意味着牛牛必须一次性决定是否申请更换每节课的教室，而不能根据某些课程的申请结果来决定其他课程是否申请；牛牛可以申请自己最希望更换教室的 mm 门课程，也可以不用完这 mm 个申请的机会，甚至可以一门课程都不申请。

因为不同的课程可能会被安排在不同的教室进行，所以牛牛需要利用课间时间从一间教室赶到另一间教室。

牛牛所在的大学有 vv 个教室，有 ee 条道路。每条道路连接两间教室，并且是可以双向通行的。由于道路的长度和拥堵程度不同，通过不同的道路耗费的体力可能会有所不同。当第 ii（1 \leq i \leq n-11≤i≤n−1）节课结束后，牛牛就会从这节课的教室出发，选择一条耗费体力最少的路径前往下一节课的教室。

现在牛牛想知道，申请哪几门课程可以使他因在教室间移动耗费的体力值的总和的期望值最小，请你帮他求出这个最小值。

输入输出格式

输入格式：

第一行四个整数 n,m,v,en,m,v,e。nn 表示这个学期内的时间段的数量；mm 表示牛牛最多可以申请更换多少节课程的教室；vv 表示牛牛学校里教室的数量；ee表示牛牛的学校里道路的数量。

第二行 nn 个正整数，第 ii（1 \leq i \leq n1≤i≤n）个正整数表示 c_ici，即第 ii 个时间段牛牛被安排上课的教室；保证 1 \le c_i \le v1≤ci≤v。

第三行 nn 个正整数，第 ii（1 \leq i \leq n1≤i≤n）个正整数表示 d_idi，即第 ii 个时间段另一间上同样课程的教室；保证 1 \le d_i \le v1≤di≤v。

第四行 nn 个实数，第 ii（1 \leq i \leq n1≤i≤n）个实数表示 k_iki，即牛牛申请在第 ii 个时间段更换教室获得通过的概率。保证 0 \le k_i \le 10≤ki≤1。

接下来 ee 行，每行三个正整数 a_j, b_j, w_jaj,bj,wj，表示有一条双向道路连接教室 a_j, b_jaj,bj，通过这条道路需要耗费的体力值是 w_jwj；保证 1 \le a_j, b_j \le v1≤aj,bj≤v， 1 \le w_j \le 1001≤wj≤100。

保证 1 \leq n \leq 20001≤n≤2000，0 \leq m \leq 20000≤m≤2000，1 \leq v \leq 3001≤v≤300，0 \leq e \leq 900000≤e≤90000。

保证通过学校里的道路，从任何一间教室出发，都能到达其他所有的教室。

保证输入的实数最多包含 33 位小数。

输出格式：

输出一行，包含一个实数，四舍五入精确到小数点后恰好22位，表示答案。你的输出必须和标准输出完全一样才算正确。

测试数据保证四舍五入后的答案和准确答案的差的绝对值不大于 4 \times 10^{-3}4×10−3。（如果你不知道什么是浮点误差，这段话可以理解为：对于大多数的算法，你可以正常地使用浮点数类型而不用对它进行特殊的处理）

输入输出样例

输入样例#1：复制

3 2 3 3

2 1 2

1 2 1

0.8 0.2 0.5

1 2 5

1 3 3

2 3 1

输出样例#1：复制

2.80

说明

【样例1说明】

所有可行的申请方案和期望收益如下表:

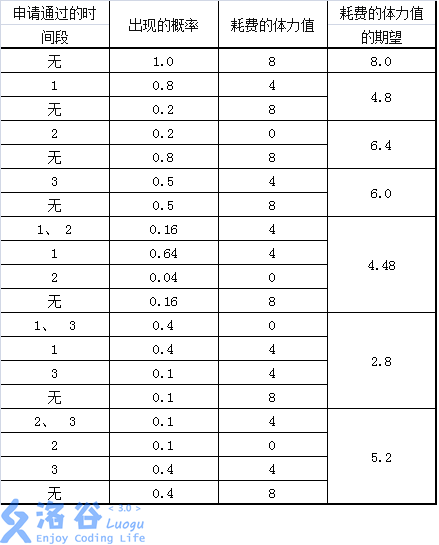
【提示】

道路中可能会有多条双向道路连接相同的两间教室。也有可能有道路两端连接的是同一间教室。
请注意区分n,m,v,e的意义, n不是教室的数量, m不是道路的数量。

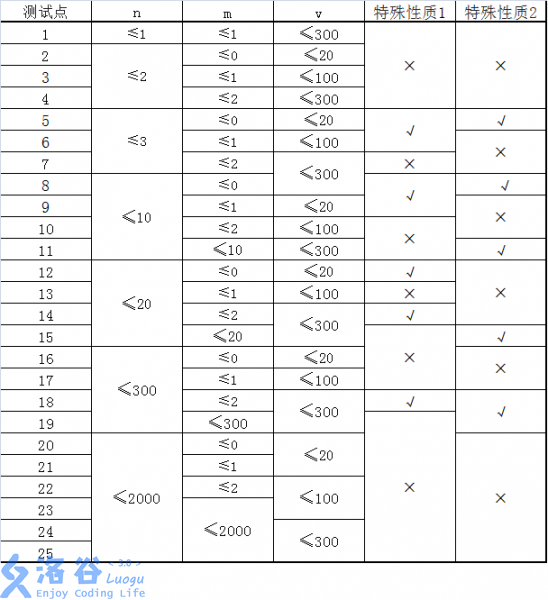
特殊性质1:图上任意两点 a_iai, b_ibi, a_iai≠ b_ibi间,存在一条耗费体力最少的路径只包含一条道路。

特殊性质2:对于所有的 1≤ i≤ n1≤i≤n， k_i= 1ki=1 。

题解

首先在读题的时候没弄清楚那个体力值是什么鬼东西......以为是路上最大拥挤度为体力值呢（手动狗头

就先跑一遍floyd预处理出两点间的最小距离，

然后按照上课顺序去dp。

设$f[i][j][0]$为在第$i$节课，已经申请了$j$次，当前没有申请的最小期望；

$f[i][j][1]$为当前申请了的最小期望。

那么转移方程就很好写了（吧

f[i][j][]=min(f[i-][j][]+dis[c[i-]][c[i]],

               f[i-][j][]+k[i-]*dis[d[i-]][c[i]]+(-k[i-])*dis[c[i-]][c[i]]);

如果上节课没有申请，那么期望直接加上距离；

如果上节课申请了，那么有$k_{i-1}$的几率上节课在$d_{i-1}$教室，有$1-k_{i-1}$的概率在$c_{i-1}$教室。

$f[i][j][1]$的情况数要多点儿，但也不难懂：

f[i][j][]=min(f[i-][j-][]+k[i]*dis[c[i-]][d[i]]+(-k[i])*dis[c[i-]][c[i]],

               f[i-][j-][]+k[i-]*k[i]*dis[d[i-]][d[i]]+k[i-]*(-k[i])*dis[d[i-]][c[i]]

                             +(-k[i-])*k[i]*dis[c[i-]][d[i]]+(-k[i-])*(-k[i])*dis[c[i-]][c[i]]);

然后按顺序往下滚就行了。

初始化$f$数组为INF，$f[1][0][0]=f[1][1][1]=0$。

//之前的写法是先把$j=0$的情况预处理出来，不知道为什么会88分，大概是访问到了一些奇怪的点为0？

 /*

 qwerta

 P1850 换教室 Accepted

 100

 代码 C++，1.43KB

 提交时间 2018-11-06 21:29:35

 耗时/内存 2170ms, 65720KB

 */

 #include<iostream>

 #include<cstring>

 #include<cstdio>

 #include<cmath>

 using namespace std;

 int c[];

 int d[];

 double k[];

 struct emm{

     int e,f,l;

 }a[];

 int h[];

 int tot=;

 int dis[][];

 double s[][][];

 const double INF=;

 #define LL long long

 int main()

 {

     //freopen("a.in","r",stdin);

     int n,m,v,e;

     cin>>n>>m>>v>>e;

     if(n==){cout<<"0.00";return ;}

     for(int i=;i<=n;++i)

     cin>>c[i];

     for(int i=;i<=n;++i)

     cin>>d[i];

     for(int i=;i<=n;++i)

     cin>>k[i];

     //

     memset(dis,,sizeof(dis));//初始化dis为INF

     //

     for(int i=;i<=e;++i)

     {

         int x,y;

         int l;

         cin>>x>>y>>l;

         dis[x][y]=min(dis[x][y],l);//有重边，所以取min

         dis[y][x]=dis[x][y];

     }

     //floyd

     for(int i=;i<=v;++i)

     dis[i][i]=;

     for(int z=;z<=v;++z)

     for(int i=;i<=v;++i)

     for(int j=;j<=v;++j)

     if(dis[i][j]>(LL)dis[i][z]+dis[z][j])

       dis[i][j]=dis[i][z]+dis[z][j];

     //

     memset(s,,sizeof(s));

     s[][][]=s[][][]=;

     for(int j=;j<=m;++j)//先循环j，好像反过来也没什么问题吧qwq

     {

         for(int i=;i<=n;++i)

         {

             s[i][j][]=min(s[i-][j][]+dis[c[i-]][c[i]],

                            s[i-][j][]+k[i-]*dis[d[i-]][c[i]]+(-k[i-])*dis[c[i-]][c[i]]);

             s[i][j][]=min(s[i-][j-][]+k[i]*dis[c[i-]][d[i]]+(-k[i])*dis[c[i-]][c[i]],

                            s[i-][j-][]+k[i-]*k[i]*dis[d[i-]][d[i]]+k[i-]*(-k[i])*dis[d[i-]][c[i]]

                                          +(-k[i-])*k[i]*dis[c[i-]][d[i]]+(-k[i-])*(-k[i])*dis[c[i-]][c[i]]);

         }

     }

     double ans=INF;

     for(int j=;j<=m;++j)//不一定要用完申请机会

     ans=min(ans,min(s[n][j][],s[n][j][]));

     printf("%.2f",ans);

     return ;

 }