Codecraft-17 and Codeforces Round #391 (Div. 1 + Div. 2, combined) C

It's that time of the year, Felicity is around the corner and you can see people celebrating all around the Himalayan region. The Himalayan region has n gyms. The i-th gym has gi Pokemon in it. There are m distinct Pokemon types in the Himalayan region numbered from 1 to m. There is a special evolution camp set up in the fest which claims to evolve any Pokemon. The type of a Pokemon could change after evolving, subject to the constraint that if two Pokemon have the same type before evolving, they will have the same type after evolving. Also, if two Pokemon have different types before evolving, they will have different types after evolving. It is also possible that a Pokemon has the same type before and after evolving.

Formally, an evolution plan is a permutation f of {1, 2, ..., m}, such that f(x) = y means that a Pokemon of type x evolves into a Pokemon of type y.

The gym leaders are intrigued by the special evolution camp and all of them plan to evolve their Pokemons. The protocol of the mountain states that in each gym, for every type of Pokemon, the number of Pokemon of that type before evolving any Pokemon should be equal the number of Pokemon of that type after evolving all the Pokemons according to the evolution plan. They now want to find out how many distinct evolution plans exist which satisfy the protocol.

Two evolution plans f1 and f2 are distinct, if they have at least one Pokemon type evolving into a different Pokemon type in the two plans, i. e. there exists an i such that f1(i) ≠ f2(i).

Your task is to find how many distinct evolution plans are possible such that if all Pokemon in all the gyms are evolved, the number of Pokemon of each type in each of the gyms remains the same. As the answer can be large, output it modulo 10⁹ + 7.

Input

The first line contains two integers n and m (1 ≤ n ≤ 10⁵, 1 ≤ m ≤ 10⁶) — the number of gyms and the number of Pokemon types.

The next n lines contain the description of Pokemons in the gyms. The i-th of these lines begins with the integer gi (1 ≤ gi ≤ 10⁵) — the number of Pokemon in the i-th gym. After that gi integers follow, denoting types of the Pokemons in the i-th gym. Each of these integers is between 1 and m.

The total number of Pokemons (the sum of all gi) does not exceed 5·10⁵.

Output

Output the number of valid evolution plans modulo 10⁹ + 7.

Examples

input

2 3
2 1 2
2 2 3

output

1

input

1 3
3 1 2 3

output

6

input

2 4
2 1 2
3 2 3 4

output

2

input

2 2
3 2 2 1
2 1 2

output

1

input

3 7
2 1 2
2 3 4
3 5 6 7

output

24

Note

In the first case, the only possible evolution plan is:

In the second case, any permutation of (1,  2,  3) is valid.

In the third case, there are two possible plans:

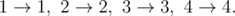
In the fourth case, the only possible evolution plan is: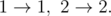

题意：有n个道馆，每个道馆的宠物可以进化，但必须每个道馆保证进化前后的种类数目一样，问有多少种进化方式（进化为f(x)=y 比如f(1)=2,1变成2 ）

解法：

1 其实根据样列，我们发现 重复的宠物可以通过内部全排列

1 2  3

2  3 ，2 3是重复的，我们有2！

2 对于不重复的，也可以通过全排列

1  2  3

　2   3  4  5 （4,5）

　　　　      6  7 ， （6,7）应该是1*2！*2！*2！

这样就考虑哪些是重复的，哪些是独有的就行

然后vector居然可以...比较相等

 #include <bits/stdc++.h>
 using namespace std;
 #define pb push_back
 typedef long long LL;
 const int mod = 1e9+;
 const int maxn =  + ;
 vector<int>a[maxn];
 int n,m;
 int main(){
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++){
         int x;
         scanf("%d",&x);
         for(int j=;j<=x;j++){
             int num;
             scanf("%d",&num);
             a[num].push_back(i);
         }
     }
     sort(a+,a++m);

     long long ans=;
     long long pos=;
     for(int i=;i<=m;i++){
         if(a[i-]==a[i]){
             pos++;  // cout<<pos<<end
             ans=(ans*pos)%mod;

         }else{
             pos=;
         }
        // cout<<ans<<endl;
     }
     printf("%lld\n",ans%mod);
     return ;
 }