标注偏置问题(Label Bias Problem)和HMM、MEMM、CRF模型比较<转>

转自http://blog.csdn.net/lskyne/article/details/8669301

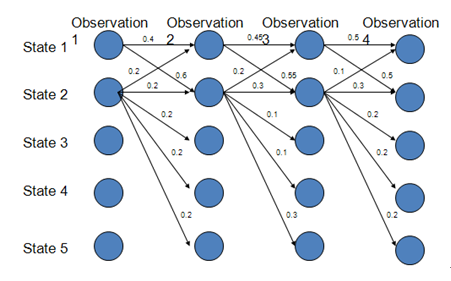
路径1-1-1-1的概率：0.4*0.45*0.5=0.09

路径2-2-2-2的概率:0.018

路径1-2-1-2:0.06

路径1-1-2-2:0.066

由此可得最优路径为1-1-1-1

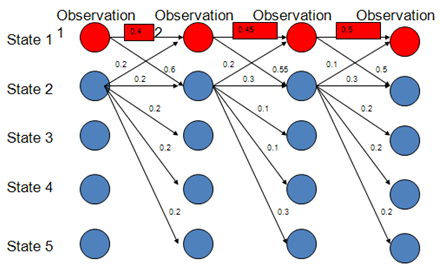
而实际上，在上图中，状态1偏向于转移到状态2，而状态2总倾向于停留在状态2，这就是所谓的标注偏置问题，由于分支数不同，概率的分布不均衡，导致状态的转移存在不公平的情况。

PS：标注偏置问题存在于最大熵马尔可夫模型（MEMM）中，虽然MEMM解决了HMM输出独立性假设的问题，但是只解决了观察值独立的问题，状态之间的假设则是标注偏置问题产生的根源，CRF则解决了标注偏置问题，是HMM模型的进一步优化。

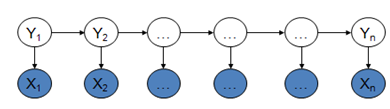
HMM模型中存在两个假设：一是输出观察值之间严格独立，二是状态的转移过程中当前状态只与前一状态有关(一阶马尔可夫模型)。

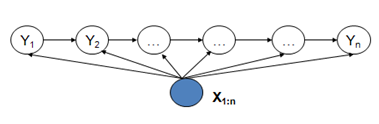
MEMM模型克服了观察值之间严格独立产生的问题，但是由于状态之间的假设理论，使得该模型存在标注偏置问题。

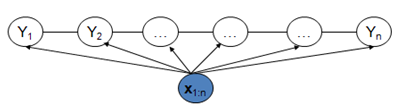
CRF模型解决了标注偏置问题，去除了HMM中两个不合理的假设，当然，模型相应得也变复杂了。

 

这三个模型都可以用来做序列标注模型。但是其各自有自身的特点，HMM模型是对转移概率和表现概率直接建模，统计共现概率。而MEMM模型是对转移概率和表现概率建立联合概率，统计时统计的是条件概率。MEMM容易陷入局部最优，是因为MEMM只在局部做归一化，而CRF模型中，统计了全局概率，在做归一化时，考虑了数据在全局的分布，而不是仅仅在局部归一化，这样就解决了MEMM中的标记偏置的问题。

举个例子，对于一个标注任务，“我爱北京天安门“，

标注为" s s  b  e b c e"

对于HMM的话，其判断这个标注成立的概率为 P= P(s转移到s)*P('我'表现为s)* P(s转移到b)*P('爱'表现为s)* ...*P().训练时，要统计状态转移概率矩阵和表现矩阵。

对于MEMM的话，其判断这个标注成立的概率为 P= P(s转移到s|'我'表现为s)*P('我'表现为s)* P(s转移到b|'爱'表现为s)*P('爱'表现为s)*..训练时，要统计条件状态转移概率矩阵和表现矩阵。

对于CRF的话，其判断这个标注成立的概率为 P= F(s转移到s,'我'表现为s)....F为一个函数，是在全局范围统计归一化的概率而不是像MEMM在局部统计归一化的概率。

HMMs(隐马尔科夫模型):

状态序列不能直接被观测到(hidden)；
     每一个观测被认为是状态序列的随机函数；
     状态转移矩阵是随机函数，根据转移概率矩阵来改变状态。
     HMMs与MRF的区别是只包含标号场变量，不包括观测场变量。

MRF(马尔科夫随机场)
     将图像模拟成一个随机变量组成的网格。
     其中的每一个变量具有明确的对由其自身之外的随机变量组成的近邻的依赖性(马尔科夫性)。

CRF(条件随机场),又称为马尔可夫随机域
     一种用于标注和切分有序数据的条件概率模型。
     从形式上来说CRF可以看做是一种无向图模型，考察给定输入序列的标注序列的条件概率。

CRF，HMM和MEHMM是在序列标注中常用的三种模型，但是也各有优缺点，现在从以下几个方面进行以下比较：

1）生成式模型or判别式模型（假设 o 是观察值，m 是模型。）

a）生成式模型：无穷样本 -> 概率密度模型 = 产生式模型 -> 预测

如果对 P(o|m) 建模，就是生成式模型。其基本思想是首先建立样本的概率密度模型，再利用模型进行推理预测。要求已知样本无穷或尽可能的大限制。这种方法一般建立在统计力学和 Bayes 理论的基础之上。

HMM模型对转移概率和表现概率直接建模，统计共同出现的概率，是一种生成式模型。

　　b）判别式模型：有限样本 -> 判别函数 = 判别式模型 -> 预测

如果对条件概率 P(m|o) 建模，就是判别模型。其基本思想是有限样本条件下建立判别函数，不考虑样本的产生模型，直接研究预测模型。代表性理论为统计学习理论。

CRF是一种判别式模型。MEMM不是一种生成式模型，它是一种基于下状态分类的有限状态模型。

2）拓扑结构

HMM和MEMM是一种有向图，CRF是一种无向图

3）全局最优or局部最优

HMM对转移概率和表现概率直接建模，统计共现概率。

MEMM是对转移概率和表现概率建立联合概率，统计时统计的是条件概率，由于其只在局部做归一化，所以容易陷入局部最优。

CRF是在全局范围内统计归一化的概率，而不像是MEMM在局部统计归一化概率。是全局最优的解。解决了MEMM中标注偏置的问题。

4）优缺点比较

优点：

a）与HMM比较。CRF没有HMM那样严格的独立性假设条件，因而可以容纳任意的上下文信息。特征设计灵活（与ME一样）

b）与MEMM比较。由于CRF计算全局最优输出节点的条件概率，它还克服了最大熵马尔可夫模型标记偏置（Label-bias）的缺点。

c）与ME比较。CRF是在给定需要标记的观察序列的条件下，计算整个标记序列的联合概率分布，而不是在给定当前状态条件下，定义下一个状态的状态分布。

缺点：

训练代价大、复杂度高