[学习笔记]分治FFT

一般的分治FFT是指：

https://www.luogu.org/problemnew/show/P4721

考虑后面的f和前面的f有关系，但是贡献可以分着计算，逐一累计上去。

考虑cdq分治。算出前面的[1,mid]的f之后，可以直接一次NTT，把后面[mid+1,r]的f的一部分算出来，累加上去。

对于后面的部分，发现都是一个前缀没有计算上。继续分治下去即可。

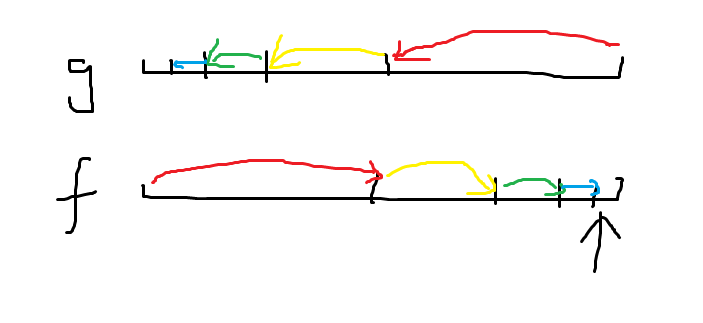
画个图就是这样。

细节注意：

1.边界，

2.0~n-1

3.四倍N的数组

4.注意之后每次都是NTT一个前缀。

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
#define int long long
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=1e5+;
const int mod=;
const int G=;
const int GI=;
int n,m;
ll qm(ll x,ll y){
    ll ret=;
    while(y){
        if(y&) ret=ret*x%mod;
        x=x*x%mod;
        y>>=;
    }
    return ret;
}
int rev[*N];
void fft(int *a,int n,int c){
    for(reg i=;i<=n-;++i){
        if(i<rev[i]) swap(a[i],a[rev[i]]);
    }
    for(reg p=;p<=n;p<<=){
        ll gen;
        if(c==) gen=qm(G,(mod-)/p);
        else gen=qm(GI,(mod-)/p);
        for(reg l=;l<n;l+=p){
            ll lp=;
            for(reg k=l;k<l+p/;++k){
                ll tmp=a[k+p/];
                a[k+p/]=(a[k]-tmp*lp%mod+mod)%mod;
                a[k]=(a[k]+tmp*lp%mod)%mod;
                lp=lp*gen%mod;
            }
        }
    }
}

ll g[*N],f[*N],c[*N],d[*N];
void calc(int *a,int *b,int n){
    for(reg i=;i<n;++i){
        rev[i]=(rev[i>>]>>)|((i&)?n>>:);
    }
    fft(a,n,);fft(b,n,);
    for(reg i=;i<n;++i) b[i]=a[i]*b[i]%mod;
    fft(b,n,-);
    ll inv=qm(n,mod-);
    for(reg i=;i<n;++i) b[i]=b[i]*inv%mod;
}
void divi(int l,int r,int L,int R){
    //cout<<" divi "<<l<<" "<<r<<" and "<<L<<" "<<R<<endl;
    if(l==r){
        return;
    }
    int mid=(l+r)>>;
    int Md=(L+R)>>;
    divi(l,mid,L,Md);

    //cout<<" bac to "<<l<<" "<<r<<endl;
    for(reg i=l;i<=mid;++i) c[i-l]=f[i];
    for(reg i=mid+;i<=r;++i) c[i-l]=;
    for(reg i=L;i<=R;++i) d[i-L]=g[i];
    for(reg i=r-l+;i<=(r-l+)*-;++i) c[i]=d[i]=;
    calc(c,d,(r-l+)*);
    for(reg i=mid+;i<=r;++i) f[i]=(f[i]+d[i-l])%mod;
    //cout<<" f[4] "<<f[4]<<" f[5] "<<f[5]<<endl;

    divi(mid+,r,L,Md);
}
int main(){
    rd(n);
    int lp=n;
    for(reg i=;i<n;++i) rd(g[i]);
    g[]=;f[]=;
    for(m=n,n=;n<m;n<<=);
    divi(,n-,,n-);
    for(reg i=;i<lp;++i){
        printf("%lld ",f[i]);
    }
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2018/12/21 14:08:16
*/

配赠福利：

一、

升级版：真的分治fft（这个代码我觉得如果有l>=r-l+1，那么可以直接return掉，后面[l,mid]*[l,mid]没有意义。）

现在的g变成了f，直接刚才那样cdq，会出现一些mid+1~r区间的f还要贡献，但是我们目前没有计算出来

还是考虑cdq分治

假设计算出来了[l,mid],那么，先把[l,mid]*[l,mid]的多项式的贡献计算出来

剩下没有算出来的怎么补？

每个值剩下的没有计算的部分，其右部分没有被计算到的区间，一定是一个l>=r-l+1的区间

如果有l>=r-l+1，那么把f[0,r-l]*f[l,mid]再计算一下，然后*2（其实本质上是补全第一次乘漏的部分）

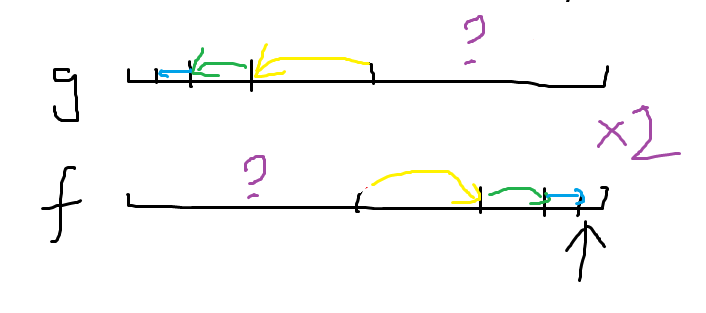
是一种延迟处理的方法，因为先算的话，有一半没有计算出来；而反过来再算的时候，涉及到的f就已经都算完了。恰好，两边对称，所以*2解决。

二、

分治FFT字面意思理解一下的话，，就是分治+FFT。。。

所以，如果要计算：

(x+a)*(x+b)*(x+c)*(x+d)*....

直接暴力算的复杂度是(2+3+4+...n)*logn

分治的话，每个(x+a)贡献的是2的长度，，一共贡献logn次，所以O(nlog^2n)