算法练习——最长公共子序列的问题(LCS)

问题描述：

对于两个序列X和Y的公共子序列中，长度最长的那个，定义为X和Y的最长公共子序列。X  Y   各自字符串有顺序，但是不一定需要相邻。

最长公共子串(Longest Common Substring )：顺序相同，并且各个字符的位置也必须相邻。

最长公共子序列(Longest Common Subsequence，LCS )：顺序形同，各个字符的位置不一定相邻。

比如：

字符串 13455 与 245576 的最长公共子序列为455
字符串 acdfg 与 adfc 的最长公共子序列为adf      adf在acdfg中的顺序相同，但是不相邻。

1：暴力求解

即对X的每一个子序列，检查它是否也是Y的子序列，从而确定它是否为X和Y的公共子序列，并且在检查过程中选出最长的公共子序列。X和Y的所有子序列都检查过后即可求出X和Y的最长公共子序列。X的一个子序列相应于下标序列{1, 2, …, m}的一个子序列，因此，X共有2m个不同子序列（Y亦如此，如为2^n，每个元素都有取或者不取的情况），从而穷举搜索法需要指数时间（2^m * 2^n）。

2：动态规划

先定义一些内容：定义两个字符串X,Y

Xi=<x1,x2.....xi>  表示字符串的 i 前缀

Yj = <y1,y2....yj> 表示字符串y的j前缀

用LCS(Xi,Yj) 表示字符串X，Y的最长公共子序列

如果：

• Xm = Yn（如果字符串X的第m位置上的字符等于字符串Y的第n个位置上的字符(下面类似，不再表述)）

则LCS(Xm,Yn) = LCS(Xm-1,Yn-1)+Xm

• Xm != Yn

则LCS(Xm,Yn) = LCS(Xm-1,Yn)   或者LCS(Xm,Yn)=LCS(Xm,Yn-1)

但是为了追求最大的公共子串则可以这么定义：LCS(Xm,Yn) = max { LCS ( Xm-1 , Yn ) , LCS( Xm , Yn-1 ) }

所以综上两种情况，我们可以得出如下的推导公式：

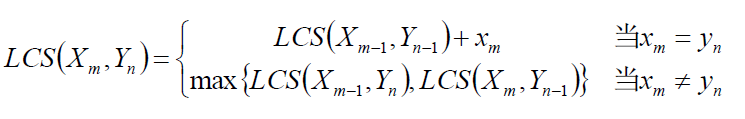
最后的最长公共子序列 ，为了将问题变成数学问题，可以这么定义上面的过程。

• 利用一个二维数组表示每一部分LCS的长度  c[m][n]
• 用c[i][j] 记录字符串Xi和Yj的最长公共子序列长度。

因此可以得到下面的推论：

为了方便表示，我们可以将字符的从1开始。

下面是一个实例图

对于 X = ABCBDAB

Y = BDCABA

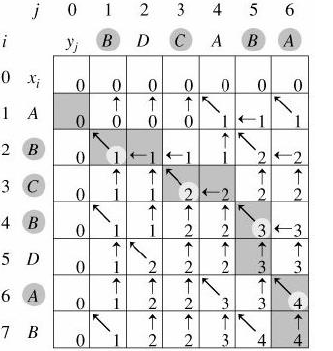
下面是具体的代码演示：

 import java.util.Stack;

 /**
  * 题目：最长公共子序列。(longest common subsequence)
  * 比如字符串a = acdfg  b =adfc  则其lcs 为 adf 。
  * 思路：可以利用动态规划的思想。
  *
  * @author Xia
  *
  */
 public class StringLCS {
     public String lsc(String s1,String s2){
         int len1 = s1.length();
         int len2 = s2.length();
         //用一个二维数组表示，这里面为了方便表示将数组行、列都扩大一个(想一想原因，可以结合上面的模式图思考)
         int[][] c = new int[len1 + 1][len2 + 1];
         //为了配合上面的增加一列，字符串中也应该增加一个字符
         s1 = ","+s1;
         s2 = "?"+s2;

         //c中的第一行第一列都赋值为0
         int i,j;
         for (i = 0; i <= len1; i++) {
             c[i][0] = 0;
         }

         for (j = 0; j <= len2; j++) {
             c[0][j] = 0;
         }
         //这里面开始遍历的时候必须从1开始
         for ( i = 1; i <= len1; i++) {
             for ( j = 1; j <= len2; j++) {
                 if (s1.charAt(i) == s2.charAt(j)) {
                     c[i][j] = c[i-1][j-1]+ 1;
                 }else {
                     c[i][j] = Math.max(c[i-1][j], c[i][j-1]);
                 }
             }
         }
         //--------------两层for循环结束后即可得到最长公共子序列的长度

         //--------------开始求解最长公共子序列------------------
         //从求好的二维数组末端开始向前寻找,那么为了最后能够最长的输出子序列，需要定义一个stack
         i = len1;
         j = len2;
         Stack<Character> s = new Stack<Character>();
         while (i != 0 && j != 0) {
             if (s1.charAt(i) == s2.charAt(j)) {
                 s.push(s1.charAt(i));
                 i--;
                 j--;
             }else {
                 if (c[i][j-1] > c[i-1][j]) {
                     j--;
                 }else {
                     i--;
                 }
             }
         }
         //-------------到这一步，已经求好了最长公共子序列并且存储在stack中
         StringBuilder sb = new StringBuilder();
         while (!s.isEmpty()) {
             sb.append(s.pop());
         }
         return sb.toString();
     }

 }

测试类：

public class Test {
    public static void main(String[] args) {
        StringLCS lcs = new StringLCS();
        String s1 = "acdfg";
        String s2 = "adcf";
        String result = lcs.lsc(s1, s2);
        System.out.println(result);　　　　//acf
    }
}

总结：根据最后的结论，多运行几次我们可以看到，其实最长公共子序列是可以有多种情况的。

还会继续更新关于其他的字符串的操作算法演示。