【BZOJ1502】【NOI2005】月下柠檬树 simpson 积分

特别提醒：eps至少要5e-6

首先我们来研究下平行光对投影的影响。

一个二维的图形，若它与光屏平行，那么不论平行光与光屏的夹角为多少，所得图形与原图形全等的（只是位置会有影响）

通过这么一分析，我们将原图形无限切片，并且投影到光屏上去，会发现阴影可以用很多很多个圆的面积并来表示。

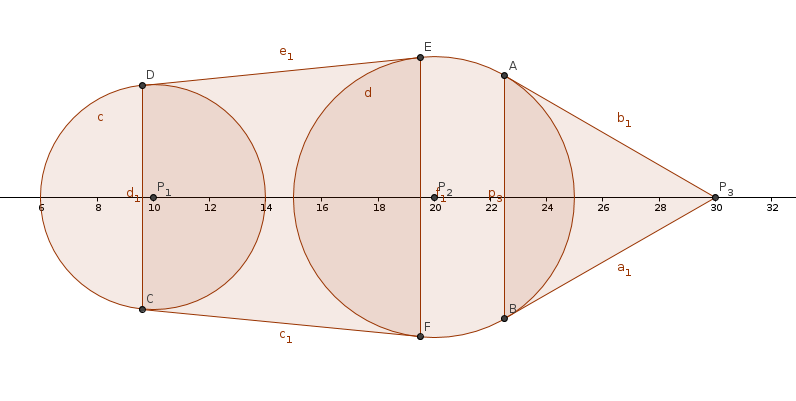
这样做显然是T的，我们进行冷静分析（雾）。通过分析得出，阴影为n个圆，n个直角梯形，和一个三角形的并。（如图所示）

在处理的时候，我们可以把三角形当梯形处理。

然后就是愉快地Simpson啦~~~~

 #include<bits/stdc++.h>
 #define eps 5e-6
 #define INF 19260817
 #define M 505
 using namespace std;
 double cx[M]={},cr[M]={};
 double lx[M]={},rx[M]={},ly[M]={},ry[M]={};
 int n;

 double f(double x){
     double maxn=;
     for(int i=;i<=n;i++){
         double deltax=abs(x-cx[i]);
         if(deltax>cr[i]) continue;
         double y=sqrt(cr[i]*cr[i]-deltax*deltax);
         maxn=max(maxn,y);
     }
     for(int i=;i<n;i++)
     if(lx[i]<=x&&x<=rx[i]){
         double k=(x-lx[i])/(rx[i]-lx[i]);
         double y=ly[i]+k*(ry[i]-ly[i]);
         maxn=max(maxn,y);
     }
     return maxn;
 }

 double get(double l,double r){
     double mid=(l+r)/;
     return (r-l)*(f(l)+*f(mid)+f(r))/;
 }

 double simpson(double l,double r){
     double mid=(l+r)/;
     double ans1=get(l,r);
     double ans2=get(l,mid)+get(mid,r);
     if(fabs(ans2-ans1)<eps) return ans2;
     return simpson(l,mid)+simpson(mid,r);
 }

 int main(){
     double l=INF,r=-INF,alpha;
     cin>>n>>alpha; n++;
     double tana=tan(alpha);
     for(int i=;i<=n;i++){
         double hh; scanf("%lf",&hh);
         hh=hh/tana;
         cx[i]=cx[i-]+hh;
     }
     for(int i=;i<=n;i++){
         if(i!=n)scanf("%lf",cr+i);
         l=min(l,cx[i]-cr[i]);
         r=max(r,cx[i]+cr[i]);
     }
     for(int i=;i<n;i++){
         double a=cx[i+]-cx[i];
         double b=cr[i+]-cr[i];
         double sita=acos(-b/a);
         lx[i]=cx[i]+cos(sita)*cr[i];
         ly[i]=      sin(sita)*cr[i];
         rx[i]=cx[i+]+cos(sita)*cr[i+];
         ry[i]=        sin(sita)*cr[i+];
     }
     double hh=simpson(l,r);
     printf("%.2lf\n",hh*);
 }