【HDU】2866：Special Prime【数论】

Special Prime

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 738    Accepted Submission(s):
390

Problem Description

Give you a prime number p, if you could find some
natural number (0 is not inclusive) n and m, satisfy the following expression: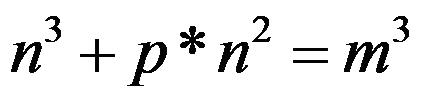

  
We call this p a
“Special Prime”.
AekdyCoin want you to tell him the number of the “Special
Prime” that no larger than L.
For example:
  If L =20
1^3 + 7*1^2 =
2^3
8^3 + 19*8^2 = 12^3
That is to say the prime number 7, 19 are two
“Special Primes”.

 

Input

The input consists of several test cases.
Every case
has only one integer indicating L.(1<=L<=10^6)

 

Output

For each case, you should output a single line indicate
the number of “Special Prime” that no larger than L. If you can’t find such
“Special Prime”, just output “No Special Prime!”

 

Sample Input

7
777

 

Sample Output

1
10

Hint

 

Source

2009
Multi-University Training Contest 7 - Host by FZU

 

Recommend

gaojie

 

Statistic | Submit | Discuss | Note

Home | Top

Hangzhou Dianzi University Online Judge 3.0 Copyright © 2005-2018 HDU ACM Team. All Rights Reserved. Designer & Developer: Wang Rongtao LinLe GaoJie GanLu Total 0.000000(s) query 1, Server time : 2018-10-18 11:20:31, Gzip enabled

Administration

---

Solution

纯数论推式子找性质辣

---

分析：$n^b + p*n^{b-1} = m^b   ==>   n^{b-1}*[n+p]=m^b$

因为$n$里面要么有$p$因子，要么没有，所以$gcd(n^{b-1},n+p)=1$或(含有p因子的数)

当$gcd(n^{b-1},n+p)== (含有p因子的数)$的时候，显然无解，因为假设有解，那么$n=K*p , K^{b-1}*p^b*(K+1)$

如果希望上面的$==m^b$,那么$K^{b-1} *(K+1)$必须能表示成某个数X的b次方，而$gcd(K,K+1)=1$,所以他们根本就没共同因

子，所以没办法表示成$X$的$b$次方，所以$gcd(n^{b-1},n+p)=1$

假设$n=x^b$，$n+p=y^b$，那么显然$m=x^{b-1}*y$，而$p=y^b-x^b$

显然$(y-x)|p$，那么必须有$y-x=1$，所以$y=x+1$，代上去就发现，$p=(x+1)^b-x ^b$。所以枚举$x$,然后判断$p$是否是素数即可。
---------------------
作者：acdreamers
来源：CSDN
原文：https://blog.csdn.net/acdreamers/article/details/8572959

---

Code

#include<bits/stdc++.h>
using namespace std;

int isnot[], prime[], t, ans[];

void init() {
    isnot[] = ;
    for(int i = ; i <= ; i ++) {
        if(!isnot[i])    prime[++t] = i;
        for(int j = ; j <= t; j ++) {
            int v = prime[j] * i;
            if(v > )    break;
            isnot[v] = ;
            if(i % prime[j] == )    break;
        }
    }
    for(int i = ; ; i ++) {
        int v = (i + ) * (i + ) * (i + ) - i * i * i;
        if(v > )    break;
        if(!isnot[v]) {
            ans[v] = ;
        }
    }
    for(int i = ; i <= ; i ++)    ans[i] += ans[i - ];
}

int main() {
    int n;
    init();
    while(scanf("%d", &n) == ) {
        if(n < )    printf("No Special Prime!\n");
        else        printf("%d\n", ans[n]);
    }
    return ;
}