[luogu]P3941 入阵曲[前缀和][压行]

[luogu]P3941

入阵曲

题目描述

小 F 很喜欢数学，但是到了高中以后数学总是考不好。

有一天，他在数学课上发起了呆；他想起了过去的一年。一年前，当他初识算法竞赛的 时候，觉得整个世界都焕然一新。这世界上怎么会有这么多奇妙的东西？曾经自己觉得难以 解决的问题，被一个又一个算法轻松解决。

小 F 当时暗自觉得，与自己的幼稚相比起来，还有好多要学习的呢。

一年过去了，想想都还有点恍惚。

他至今还能记得，某天晚上听着入阵曲，激动地睡不着觉，写题写到鸡鸣时分都兴奋不 已。也许，这就是热血吧。

也就是在那个时候，小 F 学会了矩阵乘法。让两个矩阵乘几次就能算出斐波那契数列的 第 10¹⁰⁰ 项，真是奇妙无比呢。

不过，小 F 现在可不想手算矩阵乘法——他觉得好麻烦。取而代之的，是一个简单的小 问题。他写写画画，画出了一个 n×m 的矩阵，每个格子里都有一个不超过 kk 的正整数。

小 F 想问问你，这个矩阵里有多少个不同的子矩形中的数字之和是 kk 的倍数？ 如果把一个子矩形用它的左上角和右下角描述为 (x1​,y1​,x2​,y2​)，其中x1​≤x2​,y1​≤y2​； 那么，我们认为两个子矩形是不同的，当且仅当他们以 (x1​,y1​,x2​,y2​) 表示时不同；也就是 说，只要两个矩形以 (x1​,y1​,x2​,y2​) 表示时相同，就认为这两个矩形是同一个矩形，你应该 在你的答案里只算一次。

输入输出格式

输入格式：

从标准输入中读入数据。

输入第一行，包含三个正整数 n,m,k。

输入接下来 n 行，每行包含 m 个正整数，第 i 行第 j 列表示矩阵中第 i 行第 j 列 中所填的正整数 1ai,j​。

输出格式：

输出到标准输出中。

输入一行一个非负整数，表示你的答案。

输入输出样例

输入样例1#：

2 3 2
1 2 1
2 1 2

输出样例1#：

6

说明

【样例 1 说明】

这些矩形是符合要求的： (1, 1, 1, 3)，(1, 1, 2, 2)，(1, 2, 1, 2)，(1, 2, 2, 3)，(2, 1, 2, 1)，(2, 3, 2, 3)。

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解 决一部分测试数据。

每个测试点的数据规模及特点如下表：（图来自luogu）

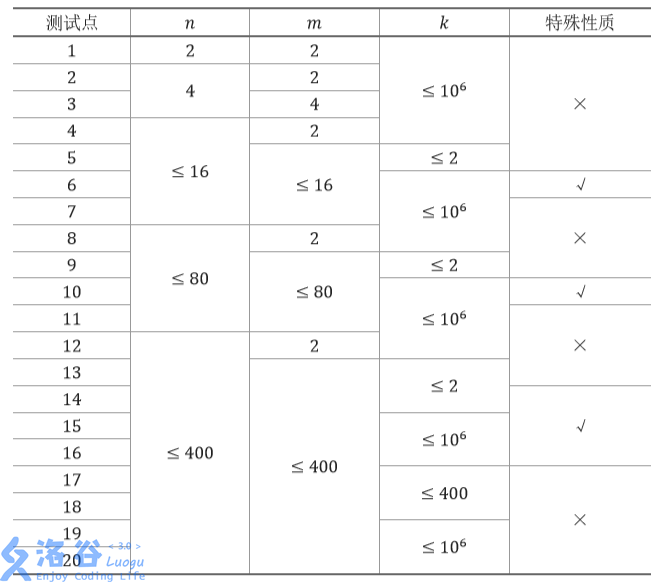
特殊性质：保证所有 ai,j​ 均相同。

---

处理前缀和，暴力枚举矩形，时间复杂度O（n⁴），得分：60。

注意到如果是一行的情况，记录r[m]表示前缀和mod k = m 的个数，贡献为：C²_r[m]，如果为m为0，还要再加上r[m]。

压行，枚举每一种列数，时间复杂度O（n³）。

代码：

 //2017.11.2
 //前缀和同余
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 using namespace std;
 typedef long long ll ;
 inline int read();
 namespace lys{
      ;
     ],find[N];
     bool used[N];
     int n,m,k;
     ll ans;
     int main(){
         int i,j,t,x,y,z;
         n=read(); m=read(); k=read();
         ;i<=n;i++)
             ;j<=m;j++){
                 a[i][j]=read(),a[i][j]=(a[i][j]+a[i-][j]+a[i][j-]-a[i-][j-]+k)%k;
             }
         ;i<=n;i++){
             ;j+i-<=n;j++){
                 memset(used,false,sizeof used);
                 ;t<=m;t++){
                     r[(a[j+i-][t]-a[j-][t]+k)%k]++;
                     find[t]=(a[j+i-][t]-a[j-][t]+k)%k;
                 }
                 ;t<=m;t++){
                     if(used[t]) continue ;
                     if(!find[t]) ans+=r[find[t]];
                     ans+=1LL*(r[find[t]]-)*(r[find[t]])/;
                     r[find[t]]=;
                     used[t]=true ;
                 }
             }
         }
         printf("%lld\n",ans);
         ;
     }
 }
 int main(){
     lys::main();
     ;
 }
 inline int read(){
     ,ff=;
     char c=getchar();
     '){
         ;
         c=getchar();
     }
     +c-',c=getchar();
     return kk*ff;
 }