[BZOJ4358]Permu(回滚莫队)

[BZOJ4358]Permu(回滚莫队)

题面

给出一个长度为n的排列P(P1,P2,...Pn)，以及m个询问。每次询问某个区间[l,r]中，最长的值域连续段长度。

分析

最简单的方法显然是用线段树维护最长值域连续段长度，复杂度\(O(n\sqrt n \log n)\),会TLE

我们以值为下标维护两个数组lb[v],rb[v]表示<v(定义为“左侧”)和>v(定义为“右侧）的连续段长度，当我们加入一个值v的时候，会产生一个长度为lb[v]+rb[v]+1的连续段,，可以用来更新答案。同时，我们需要更新lb,rb。对于v两端的连续段来说，我们不需要修改每一个值的lb,rb，只需要修改段边界的就可以了，因为下一次插入值w的时候,只有w落在某个连续段的边界上，我们才要更新答案，而更新的答案只与段边界的lb,rb有关

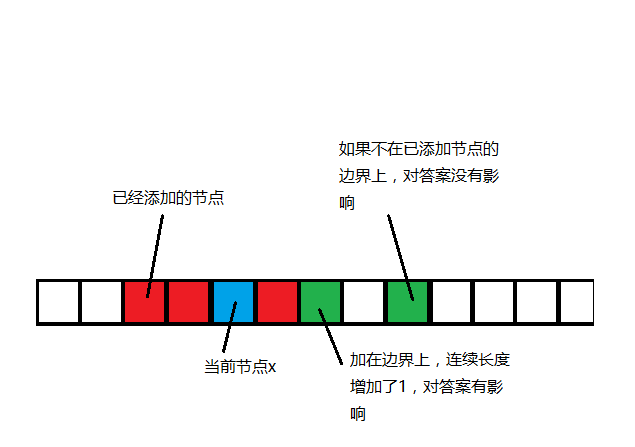
然后考虑如何莫队处理：

我们把询问以左端点块编号为第一关键字，右端点为第二关键字排序。对于一个块中的所有询问，我们发现r是递增的，所以不用撤销。而l不一定是递增的，我们要考虑如何撤销某个添加值的操作。

对于每一块，初始r设为块的右端点，然后每个询问先将r往右移，处理r和l不在同一块的询问。然后处理询问在块内之间的部分，直接暴力把询问的块内部分的所有点添加进去。修改前把原来lb,rb的值记下来，保存在栈里面。处理完这个询问之后再复原。

我们发现这样的时间复杂度和普通莫队是相同的，因为加入和撤销相当于左端点从l1移到l2,再移回来，因为在同一个块内，所以移动距离不会超过\(O(\sqrt n)\)

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define maxn 50000
#define maxm 50000
using namespace std;
inline void qread(int &x) {
	x=0;
	int sign=1;
	char c=getchar();
	while(c<'0'||c>'9') {
		if(c=='-') sign=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9') {
		x=x*10+c-'0';
		c=getchar();
	}
	x=x*sign;
}
inline void qprint(int x) {
	if(x<0) {
		putchar('-');
		qprint(-x);
	} else if(x==0) {
		putchar('0');
		return;
	} else {
		if(x>=10) qprint(x/10);
		putchar('0'+x%10);
	}
}
int n,m;
int a[maxn+5];
int bsz;
int belong[maxn+5];
struct query{
	int l;
	int bel;//减少数组寻址次数
	int r;
	int id;
	friend bool operator < (query p,query q){
		return p.bel<q.bel||(p.bel==q.bel&&p.r<q.r);
	}
}q[maxm+5]; 

int ans[maxn+5];
int rb[maxn+5],lb[maxn+5];
//记录第i向左和向右的连续段长度 

//用于撤销修改操作的栈
struct node{
	int type;//记录是哪个数组修改，1则是lb,2则是rb
	int pos;
	int val;
	node(){

	}
	node(int _type,int _pos,int _val){
		type=_type;
		pos=_pos;
		val=_val;
	}
}st[maxn+5];
int main(){
	qread(n);
	qread(m);
	for(int i=1;i<=n;i++) qread(a[i]);
	bsz=n/sqrt(m);
	for(int i=1;i<=n;i++) belong[i]=i/bsz+1;
	for(int i=1;i<=m;i++){
		qread(q[i].l);
		qread(q[i].r);
		q[i].id=i;
		q[i].bel=belong[q[i].l];
	}
	sort(q+1,q+1+m);
	int r=0;
	int sum=0;
	for(int i=1;i<=m;i++){
		if(q[i].bel!=q[i-1].bel){//新的块
			sum=0;
			for(int i=1;i<=n;i++) lb[i]=rb[i]=0;
			r=q[i].bel*bsz;
		}
		while(r<q[i].r){//如果l,r不在同一个块，把r在块外部分加入,r单调递增，可不用撤销修改
			r++;
			lb[a[r]]=lb[a[r]-1]+1;
			rb[a[r]]=rb[a[r]+1]+1;
			int tmp=lb[a[r]]+rb[a[r]]-1;
			sum=max(sum,tmp);
			//对于a[r]两端的连续段来说，我们不需要修改每一个值的lb,rb，只需要修改段边界的就可以了
			//因为下一次插入a[r]，若a[r]已经存在，则答案不变，
			//若a[r]落在某个连续段的边界上，我们才要更新答案，而更新的答案只与段边界的lb,rb有关
			lb[a[r]+rb[a[r]]-1]=tmp;
			rb[a[r]-lb[a[r]]+1]=tmp;
		}
		int res=sum;//由于撤销对sum的修改比较麻烦，移动左端点的时候不更新sum,而更新答案res
		int top=0;
		//min(q[i].r,q[i].bel*bsz)表示把询问在当前块内部分加入
		for(int l=q[i].l;l<=min(q[i].r,q[i].bel*bsz);l++){//移动左端点，要回滚
			lb[a[l]]=lb[a[l]-1]+1;
			rb[a[l]]=rb[a[l]+1]+1;
			int tmp=lb[a[l]]+rb[a[l]]-1;
			st[++top]=node(1,a[l]+rb[a[l]]-1,lb[a[l]+rb[a[l]]-1]);//修改前把原来的值记下来
			st[++top]=node(2,a[l]-lb[a[l]]+1,rb[a[l]-lb[a[l]]+1]);
			lb[a[l]+rb[a[l]]-1]=tmp;
			rb[a[l]-lb[a[l]]+1]=tmp;
			res=max(res,tmp);
		}
		for(int j=top;j>=1;j--){//撤销对连续段端点的修改
			if(st[j].type==1) lb[st[j].pos]=st[j].val;
			else rb[st[j].pos]=st[j].val;
		}
		for(int j=q[i].l;j<=min(q[i].r,q[i].bel*bsz);j++){//撤销新加入的点对lb,rb的修改
			lb[a[j]]=rb[a[j]]=0;
		}
		ans[q[i].id]=res;
	}
	for(int i=1;i<=m;i++){
		qprint(ans[i]);
		putchar('\n');
	}
}