leetcode 94二叉树的中序遍历

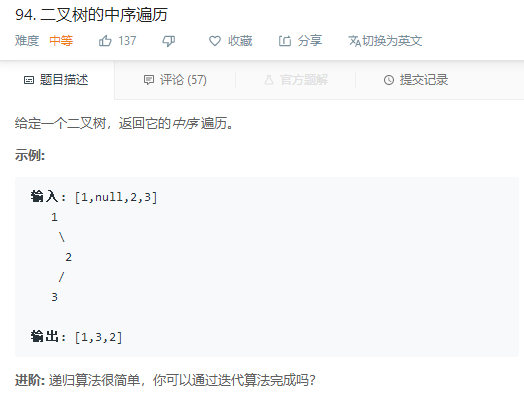
递归算法C++代码：

 /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
  * };
  */
 class Solution {
 public:
     vector<int> inorderTraversal(TreeNode* root) {
         vector<int> tra;
         Morder(root,tra);
         return tra;
     }
     void Morder(TreeNode* root,vector<int> &tra){
         if(root==NULL) return;
         if(root->left)
             Morder(root->left,tra);
         tra.push_back(root->val);
         if(root->right)
             Morder(root->right,tra);
     }
 };

非递归方法（迭代）：通过stack容器

C++代码：O(n)空间复杂度,O(n)时间复杂度

自己写的，实际上为将递归方法代码用stack具体化，需要注意的是加上了回溯与向下递归的判别；

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
/**
迭代法：具象描述递归执行过程
1）检查当前p是否为NULL,如果非NULL,当前节点入栈，只要当前节点有左子节点，左子节点入栈；
2）1之后，取栈顶元素p，由于1的操作，p没有左子节点，那么访问当前节点的值，且p出栈；
3）接下来访问右节点，p=p->right,如果右子节点存在，那么入栈，循环结束；
**/
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        if(root==NULL) return {};
        vector<int>res;
        stack<TreeNode*>s;
        TreeNode*p=root;
        s.push(p);
        while(!s.empty()){
            while(p&&p->left){
                p=p->left;s.push(p);
            }

            p=s.top();
            res.push_back(p->val);s.pop();

            //此处先令p=p->right,p可用作第一个while判断是向下递归还是回溯，如果递归过程p为非空，如果为NULl则代表回溯，那么下一轮不用向左递归；
            p=p->right;
            if(p) s.push(p);
        }
        return res;
    }
};

别人的代码：

 /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
  * };
  */
 class Solution {
 public:
     vector<int> inorderTraversal(TreeNode* root) {
         //使用栈的非递归方法
         vector<int> res;
         stack<TreeNode*> st;
         TreeNode* T=root;
         while(T||!st.empty()){
             //将T的所有左孩子入栈
             while(T){
                 st.push(T);
                 T=T->left;
             }
             //访问T的元素，然后转到T的右孩子
             if(!st.empty()){
                 T=st.top();
                 st.pop();
                 res.push_back(T->val);
                 T=T->right;
             }
         }
         return res;
     }
 };

方法三：Morris Traversal

由于需要用到Thread Binary  Tree（线索二叉树），参考 透彻理解线索二叉树 彻底理解线索二叉树

Morris Traversal方法遍历二叉树（非递归，不用栈，O(1)空间）

对于n个节点的二叉树，左右孩子指针为2n个，利用的指针为n-1个，没有利用的指针为n+1个；利用空链域存储前驱和后继：

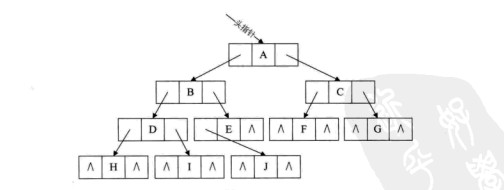
记ptr指向二叉链表中的一个结点，以下是建立线索的规则：

（1）如果ptr->lchild为空，则存放指向中序遍历序列中该结点的前驱结点。这个结点称为ptr的中序前驱；

（2）如果ptr->rchild为空，则存放指向中序遍历序列中该结点的后继结点。这个结点称为ptr的中序后继；

当然，Morris遍历只用到了线索二叉树的思想和部分操作，线索二叉树的更细节的东西此处不赘述。对于本题，实际上只用到了对叶节点的右指针的线索化，以及通过线索化的指针进行回溯。主要有以下两点：

#1 对所有叶节点的右指针的线索化，令其指向中序遍历的后继节点；

#2 通过线索化的节点，访问中序遍历的后继节点，并恢复被线索化的节点；

参考：二叉树的遍历：先序中序后序遍历的递归与非递归实现及层序遍历

C++代码如下：O(1)空间复杂度,O(n)时间复杂度

 /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
  * };
  */
 class Solution {
 public:
     vector<int> inorderTraversal(TreeNode* root) {
         //Morris Traversal：右线索化+回溯
         vector<int> res;
         if(!root) return res;
         TreeNode *p=root;

         while(p){
             //定义两个节点指针变量p和p的左孩子pLeft
           TreeNode *pLeft=p->left;
             if(pLeft){
                 //访问p的左孩子的最右子孩子（即pLeft右孩子的右孩子的右孩子...）
                 //线索化之前pLeft的最右子孩子的right指针指向NULL,
                 //线索化之后pLeft的最右子孩子的right指向中序遍历中该节点的后继节点p
                 //所以循环终止条件为pLeft->right==NULL 或 pLeft->right==p
                 while(pLeft->right && pLeft->right!=p){
                     pLeft=pLeft->right;
                 }
                 //此时pLeft代表p的左孩子的最右子孩子
                 //pLeft->right==NULL代表没有被线索化，进行线索化然后访问p的左孩子
                 if(pLeft->right==NULL){
                     pLeft->right=p;
                     p=p->left;
                     continue;
                 }
                 //pLeft->right!=NULL代表已经被线索化，此时已经回溯到原来的节点p(第2次访问)，所以要恢复被线索化的pLeft的最右子孩子
                 else{
                     pLeft->right=NULL;
                 }
             }
             res.push_back(p->val);
             p=p->right;//访问右孩子（对非叶节点），回溯到中序遍历的后续节点（对叶节点）；
             //因为线索化的操作最终是对所有的叶节点进行的，所以上述语句实际有访问右孩子和回溯两个功能；
         }
         return res;
     }
 };