MCMC,GIBBS SAMPLING简单摘要

　　本文后面很多内容都是参考博客：http://www.cnblogs.com/xbinworld/p/4266146.html。本文主要用作学习交流备忘用。

　　

1）简述：

　　随机模拟也可以叫做蒙特卡洛模拟，其中一个很重要的问题就是指定一个概率分布p(x)，然后在计算机中生成它的样本。

2）MC核心思想：

　　当我们无法精确精算和或者积分时，可以把和或者积分视作某种分布下的期望，然后通过估计对应的平均值来近似这个期望。

　　      

3）产生的问题与改进

在上述式子中，我们依赖于基本分布p(x)，而且该分部可以让我们轻易的采样。但是实际中这个条件并不都是成立的。当我们无法从p中采样时，一个方案是重要采样，另一种是使用一个趋近于目标分部估计的序列即MCMC（马尔科夫蒙塔卡洛方法）

4）重要采样的方法

　　令：p(x)f(x)=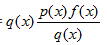。在这里我们从q中进行采样，然后估计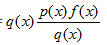的均值。

　　问题：对于上述式子，对于任意的q分布都是可行的，如果从方差最小的角度选择最优q分布，虽然能够最优q分布可以得到，但是从中采样是不可行的。但是其他的仍然能够降低方差的q还是可行的。

　　另外一个好的q分布很难取得。因为如果一个q使得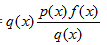很大，那么这个估计的方差也会很大。因为我们经常会取一些简单的分布作为q。但是当x是高维数据的时候，q分布的简单性很难与p或者pf相匹配。当q>>pf时候，重要采样采到了很多无用的样本（权值之和很小，或趋近于0）。当q<<pf时候，样本很少被采集到，其对应的权值会非常大。

　　尽管存在很多风险，重要采样在机器学习和深度学习中仍有重要的作用： 重要采样被应用于加速训练具有大规模词汇的神经网络语言模型的过程中或者其他有着大量输出结点的神经网络中。此外，还可以看到重要采样应用于估计配分函数（一个概率分布的归一化常数）的过程中以及在深度有向图模型比如变分自编码器中估计似然函数的对数。采用随机梯度下降训练模型参数的时候重要采样可以用来改进对代价函数梯度的估计，尤其是针对于分类器模型的训练中一小部分错误分类样本产生的代价函数。在这种情况下更加频繁地采集这些困难的样本可以降低梯度估计的误差。

5）马尔科夫链和马尔科夫稳态

　　马氏链定理：如果一个非周期马氏链具有状态转移概率矩阵P，且它的任何两个状态是联通的，那么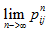存在，且与i无关（i表示初始状态），记 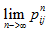=π(j)。即沿着状态转移矩阵进行转移，无论初始状态为什么，最终都会收敛到一个稳定分布π=[π(1),π(2)….]。

　　所以一个理想的情况是：找到转移矩阵为p的马氏链，使得该马氏链的平稳分布恰好是p(x)，那么我们从任一个初始状态x0出发，得到一个转移序列x1,x2,….如果其在xi处收敛，则x(i+1)…..就是我们要取的样本。

细致平稳条件：

　　

　　

　　

　　

　　此时取：

　　则有：

　　

6）MCMC-Gibbs Sampling

　　

　　Gibbs-Sampling算法：

　　

　　

　　

参考文献：

　　　　[1]http://www.cnblogs.com/xbinworld/p/4266146.html

[2]
http://blog.csdn.net/xianlingmao/article/details/7768833

　　　　[3] http://www.cnblogs.com/daniel-D/p/3388724.html

　　　　[4] http://cos.name/2013/01/lda-math-mcmc-and-gibbs-sampling/

　　　　[5] An Introduction to MCMC for Machine Learning，2003

　　　　[6] Introduction to Monte Carlo Methods

　　　　[7]深度学习