洛谷P1274-魔术数字游戏

Problem 洛谷P1274-魔术数字游戏

Accept: 118    Submit: 243
Time Limit: 1000 mSec    Memory Limit : 128MB

Problem Description

填数字方格的游戏有很多种变化，如下图所示的4×4方格中，我们要选择从数字1到16来填满这十六个格子(Aij，其中i＝1..4，j＝1..4)。为了让游戏更有挑战性，我们要求下列六项中的每一项所指定的四个格子，其数字累加的和必须为34：

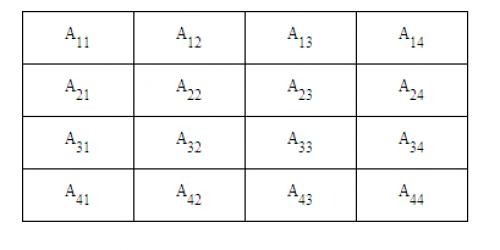
四个角落上的数字，即A11+A14+A41+A44＝34。

每个角落上的2×2方格中的数字，例如左上角：A11+A12+A21+A22＝34。

最中间的2×2方格中的数字，即A22+A23+A32+A33=34。

每条水平线上四个格子中的数字，即Ai1+Ai2+Ai3+Ai4＝34，其中i＝1..4。

每条垂直线上四个格子中的数字，即A1j+A2j+A3j+A4j＝34，其中j＝1..4。

两条对角线上四个格子中的数字，例如左上角到右下角：A11+A22+A33+A44＝34。

右上角到左下角：A14+A23+A32+A41＝34

 Input

输入文件会指定把数字1先固定在某一格内。输入的文件只有一行包含两个正数据I和J，表示第1行和第J列的格子放数字1。剩下的十五个格子，请按照前述六项条件用数字2到16来填满。

 Output

把全部的正确解答用每4行一组写到输出文件，每行四个数，相邻两数之间用一个空格隔开。两组答案之间，要以一个空白行相间，并且依序排好。排序的方式，是先从第一行的数字开始比较，每一行数字，由最左边的数字开始比，数字较小的解答必须先输出到文件中。

 

 Sample Input

1 1

Sample output

1 4 13 16
14 15 2 3
8 5 12 9
11 10 7 6

 

1 4 13 16
14 15 2 3
12 9 8 5
7 6 11 10

 

题目链接：https://www.luogu.org/problemnew/show/P1274

 

题解：无脑爆搜就好，剪枝的话就按照题目说的剪，代码比较冗长

 

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cstdlib>
 using namespace std;

 const int maxn = ;

 int gra[maxn][maxn];
 bool used[maxn*];

 void output(){
     for(int i = ;i <= ;i++){
         printf("%d",gra[i][]);
         for(int j = ;j <= ;j++){
             printf(" %d",gra[i][j]);
         }
         printf("\n");
     }
     printf("\n");
 }

 void dfs(int x,int y){
     if(x > ){
         output();
         return;
     }
     if(gra[x][y] == ){
         if(x== && y==){
             if(gra[][]+gra[][]+gra[][]+gra[][] != ) return;
         }
         if(x== && y==){
             if(gra[][]+gra[][]+gra[][]+gra[][] != ) return;
         }
         if(x== && y==){
             if(gra[][]+gra[][]+gra[][]+gra[][] != ) return;
         }
         if(x== && y==){
             if(gra[][]+gra[][]+gra[][]+gra[][] != ) return;
             if(gra[][]+gra[][]+gra[][]+gra[][] != ) return;
             if(gra[][]+gra[][]+gra[][]+gra[][] != ) return;
         }
         if(x== && y==){
             if(gra[][]+gra[][]+gra[][]+gra[][] != ) return;
         }
         if(x== && y==){
             if(gra[][]+gra[][]+gra[][]+gra[][] != ) return;
         }
         if(x == ){
             if(gra[][y]+gra[][y]+gra[][y]+gra[][y] != ) return;
         }
         if(y == ){
             if(gra[x][]+gra[x][]+gra[x][]+gra[x][] != ) return;
         }
         if(y == ) dfs(x+,);
         else dfs(x,y+);
     }
     else{
         for(int i = ;i <= ;i++){
             if(!used[i]){
                 //output();
                 gra[x][y] = i;
                 if(x== && y==){
                     if(gra[][]+gra[][]+gra[][]+gra[][] != ){
                         gra[x][y] = ;
                         continue;
                     }
                 }
                 if(x== && y==){
                     if(gra[][]+gra[][]+gra[][]+gra[][] != ){
                         gra[x][y] = ;
                         continue;
                     }
                 }
                 if(x== && y==){
                     if(gra[][]+gra[][]+gra[][]+gra[][] != ){
                         continue;
                         gra[x][y] = ;
                     }
                 }
                 if(x== && y==){
                     if(gra[][]+gra[][]+gra[][]+gra[][] != ){
                         gra[x][y] = ;
                         continue;
                     }
                     if(gra[][]+gra[][]+gra[][]+gra[][] != ){
                         gra[x][y] = ;
                         continue;
                     }
                     if(gra[][]+gra[][]+gra[][]+gra[][] != ){
                         gra[x][y] = ;
                         continue;
                     }
                 }
                 if(x== && y==){
                     if(gra[][]+gra[][]+gra[][]+gra[][] != ){
                         gra[x][y] = ;
                         continue;
                     }
                 }
                 if(x ==  && y==){
                     if(gra[][]+gra[][]+gra[][]+gra[][] != ){
                         gra[x][y] = ;
                         continue;
                     }
                 }
                 if(x == ){
                     if(gra[][y]+gra[][y]+gra[][y]+gra[][y] != ){
                         gra[x][y] = ;
                         continue;
                     }
                 }
                 if(y == ){
                     if(gra[x][]+gra[x][]+gra[x][]+gra[x][] != ){
                         gra[x][y] = ;
                         continue;
                     }
                 }
                 used[i] = true;
                 if(y == ) dfs(x+,);
                 else dfs(x,y+);
                 used[i] = false;
                 gra[x][y] = ;
             }
         }
     }
 }

 int main()
 {
     //freopen("input.txt","r",stdin);
     int x,y;
     scanf("%d%d",&x,&y);
     memset(gra,,sizeof(gra));
     memset(used,false,sizeof(used));
     gra[x][y] = ;
     used[] = true;
     dfs(,);
     return ;
 }