AVL平衡二叉树

AVL树

1、若它的左子树不为空，则左子树上所有的节点值都小于它的根节点值。

2、若它的右子树不为空，则右子树上所有的节点值均大于它的根节点值。

3、它的左右子树也分别可以充当为二叉查找树。

例如：

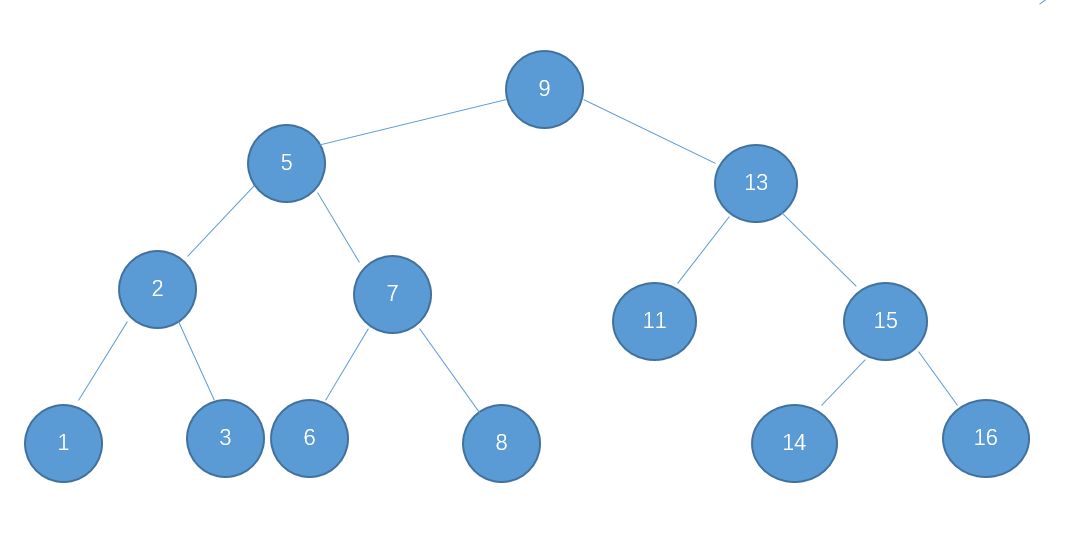
例如，我现在想要查找数值为14的节点。由于二叉查找树的特性，我们可以很快着找到它，其过程如下：

1、和根节点9比较

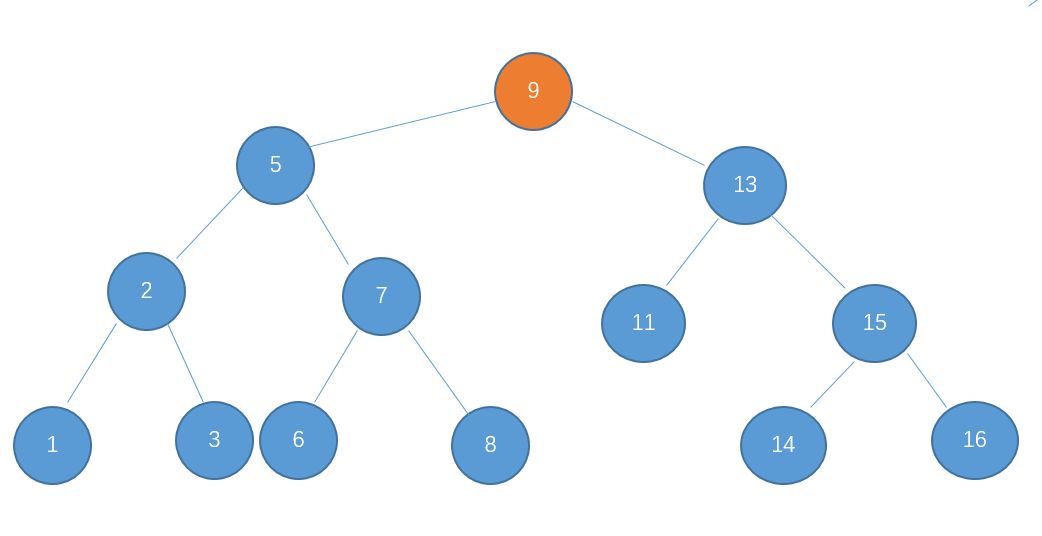
2、由于 14 > 9，所以14只可能存在于9的右子树中，因此查看右孩子13

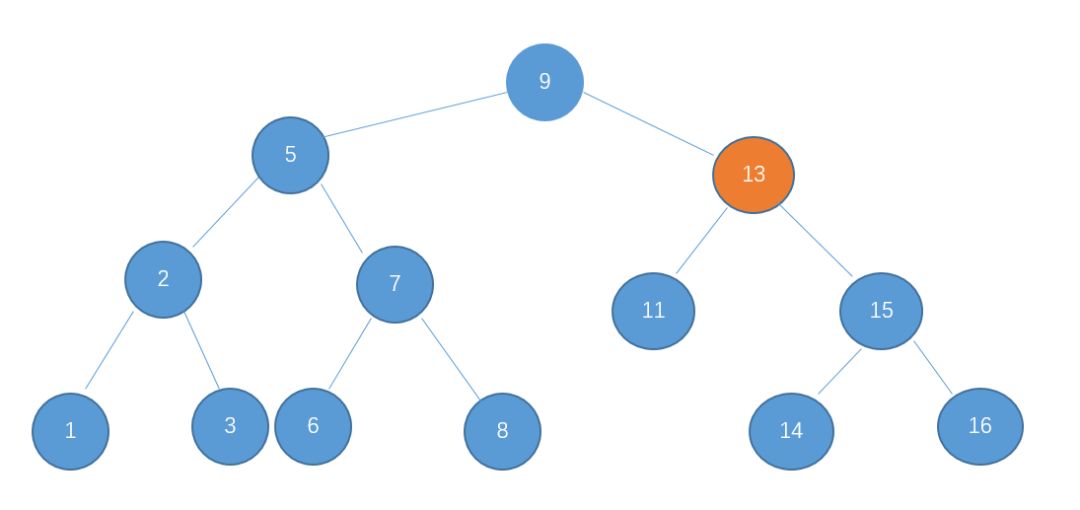
3、由于 14 > 13，所以继续查看13的右孩子15

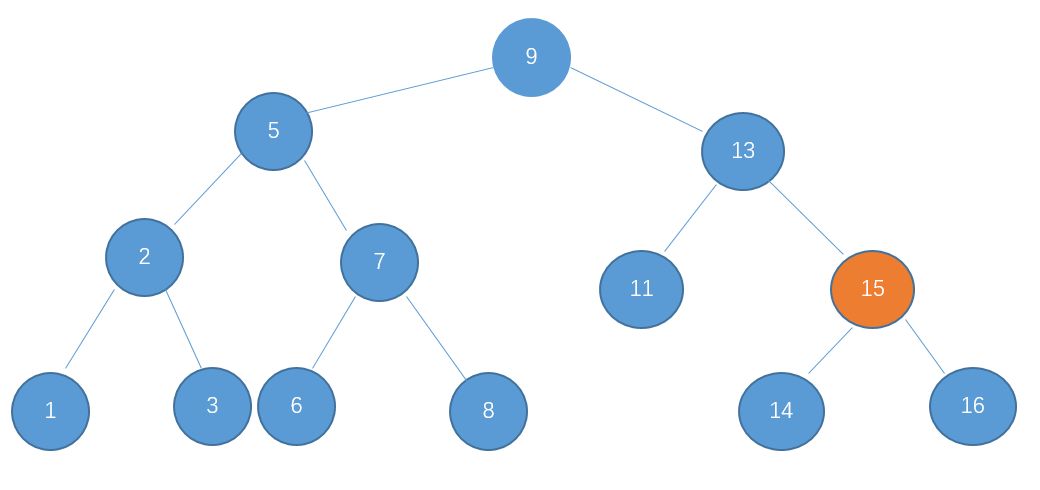
4、由于 14 < 15，所以14只可能存在于15的左孩子中，因此查找15的左孩子14

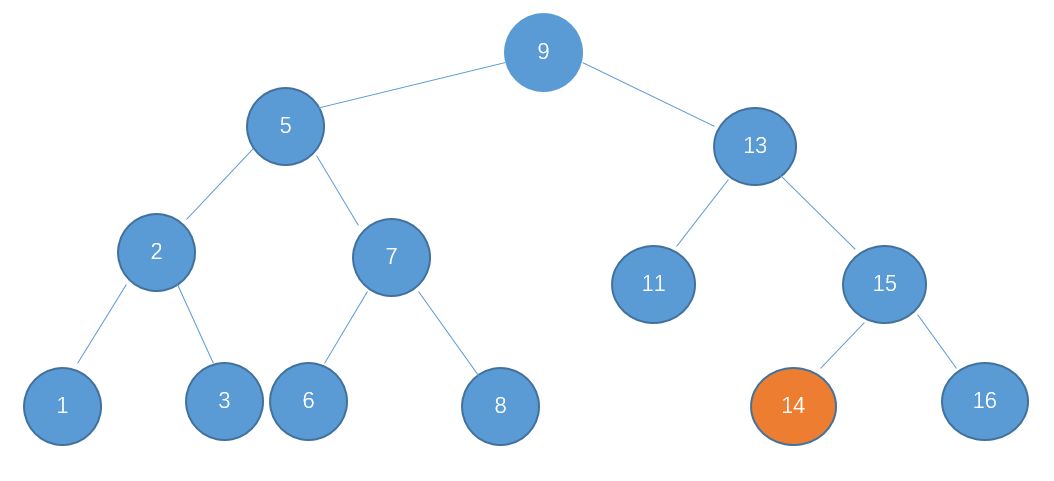
5、这时候发现14正是自己查找的值，于是查找结束。

这种查找二叉树的查找正是二分查找的思想，可以很快着找到目的节点，查找所需的最大次数等同于二叉查找树的高度。

在插入的时候也是一样，通过一层一层的比较，最后找到适合自己的位置。

初始的二叉查找树只有三个节点：

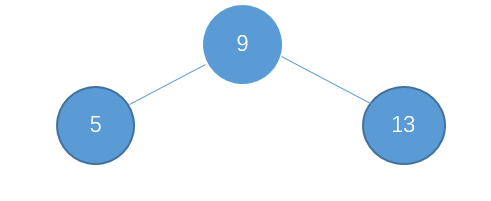
然后我们按照顺序陆续插入节点 4，3，2，1，0。插入之后的结构如下：

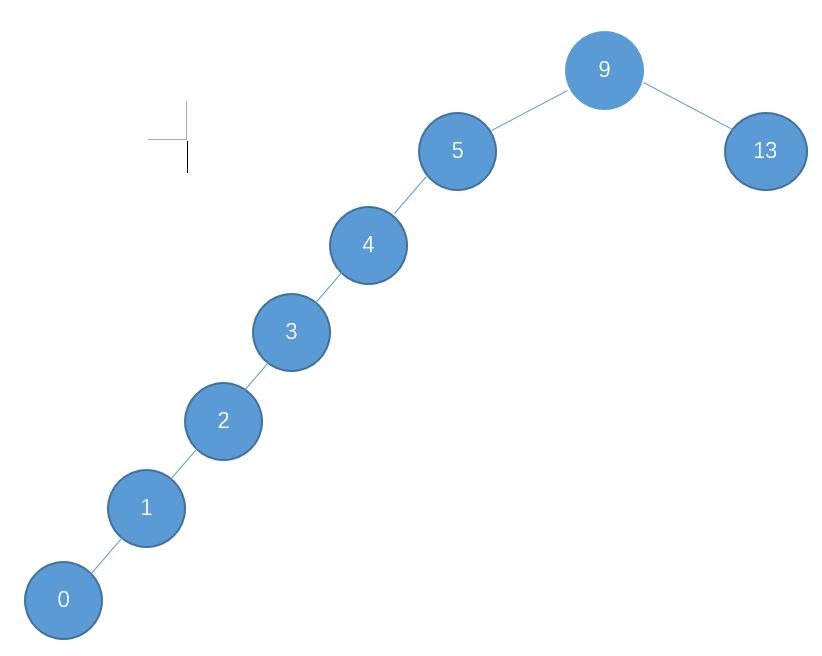
这是一种比查找二叉树还特别的树哦，这种树就可以帮助我们解决二叉查找树刚才的那种所有节点都倾向一边的缺点的。具有如下特性：

1. 具有二叉查找树的全部特性。
2. 每个节点的左子树和右子树的高度差至多等于1。

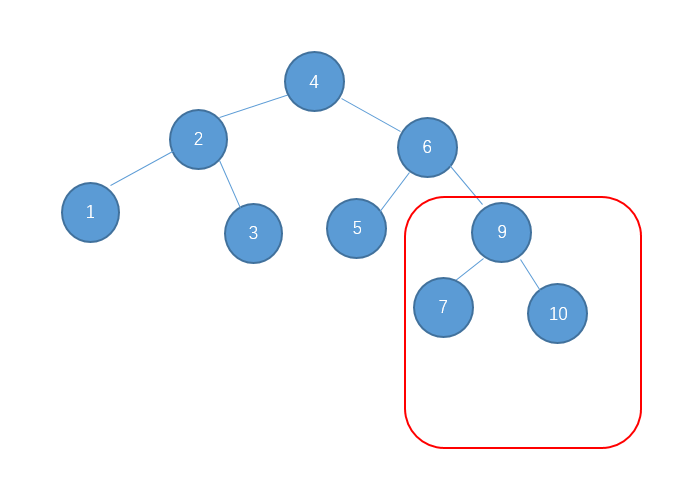
例如：图一就是一颗AVL树了，而图二则不是(节点右边标的是这个节点的高度)。

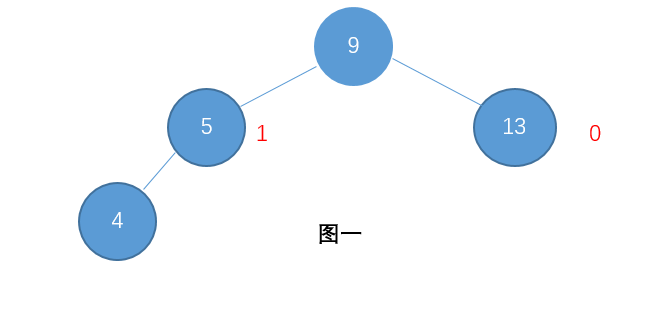
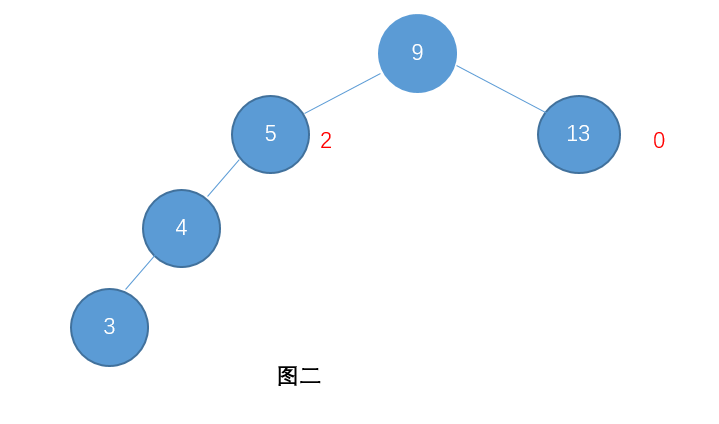
对于图二，因为节点9的左孩子高度为2，而右孩子高度为0。他们之间的差值超过1了。

这种树就可以保证不会出现大量节点偏向于一边的情况了。

左右子树的高度差都不超过1，没有要求是左边高还是右边高，那就存在以下三种情况：

　　　　注：（有的以高度为0开始，这里高度以1开始，也就是空节点高度为0，一个节点的高度为1）

　　　　如果一样高则高度一致，所以高度差为0;

　　　　如果左边高则左边比右边高，满足平衡二叉树高度不超过1，我们把高度差记为1（左子树高度减去右子树高度）;

如果右边高则右边比左边高，满足平衡二叉树高度不超过1，我们把高度差记为-1（左子树高度减去右子树高度）;

这就是平衡因子的概念，

听起来这种树还不错，可以对于图1，如果我们要插入一个节点3，按照查找二叉树的特性，我们只能把3作为节点4的左子树插进去，可是插进去之后，又会破坏了AVL树的特性，那我们那该怎么弄？

右旋

我们在进行节点插入的时候，可能会出现节点都倾向于左边的情况，例如：

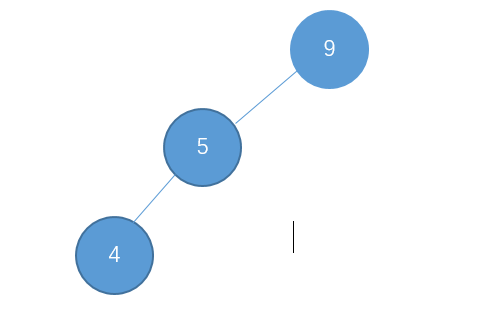
我们把这种倾向于左边的情况称之为左-左型。这个时候，我们就可以对节点9进行右旋操作，使它恢复平衡。

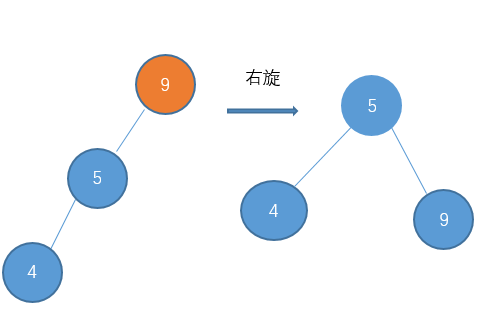
即：顺时针旋转两个节点，使得父节点被自己的左孩子取代，而自己成为自己的右孩子

再举个例子：

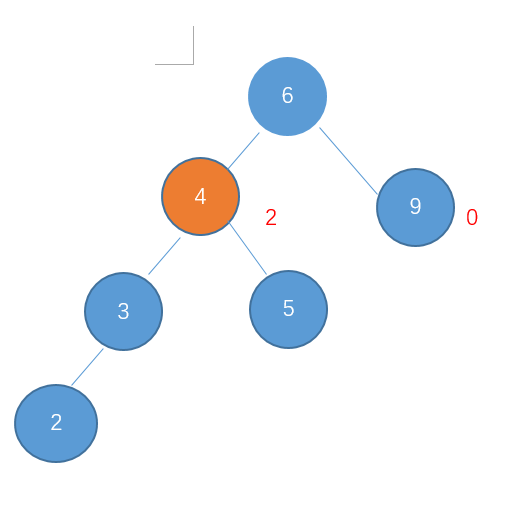
节点4和9高度相差大于1。由于是左孩子的高度较高，此时是左-左型，进行右旋。

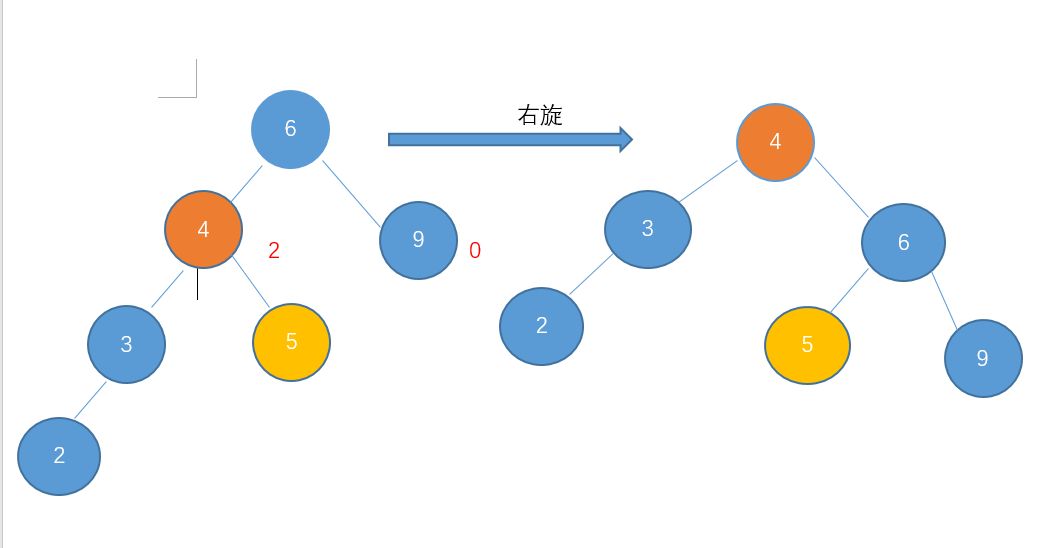
这里要注意，节点4的右孩子成为了节点6的左孩子了

我找了个动图，尽量这个动图和上面例子的节点不一样。

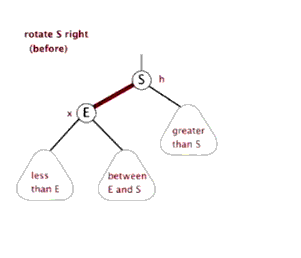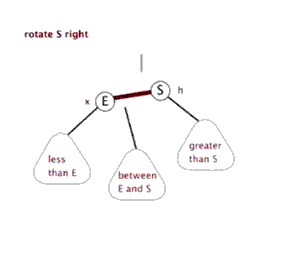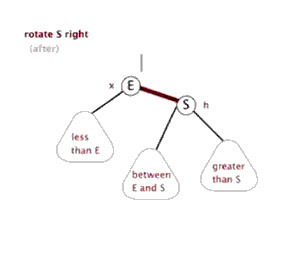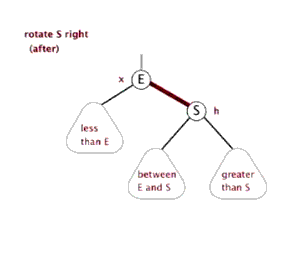
左旋

左旋和右旋一样，就是用来解决当大部分节点都偏向右边的时候，通过左旋来还原。例如：

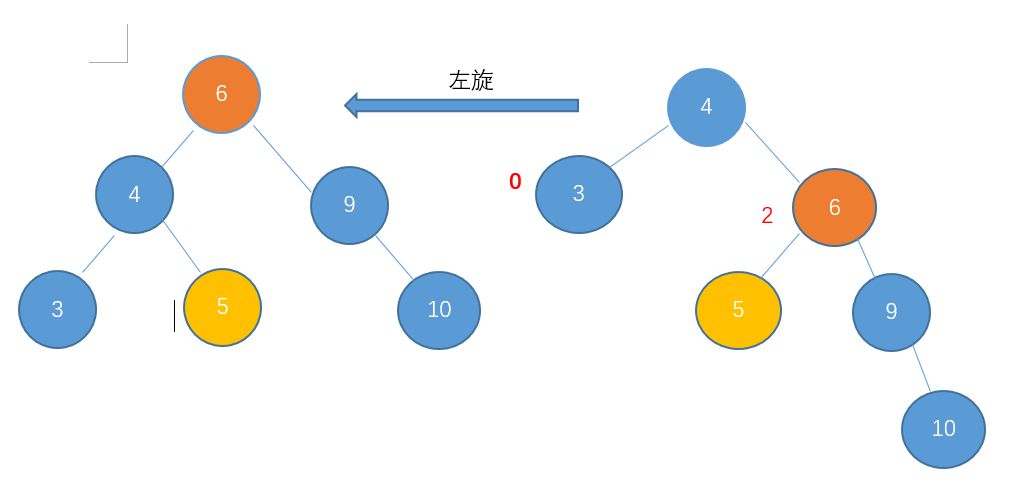
我们把这种倾向于右边的情况称之为右-右型。

我也找了一张动图。

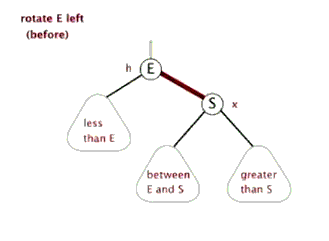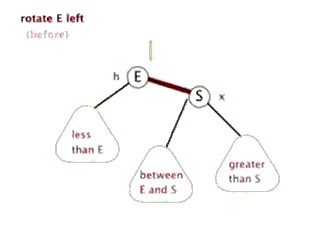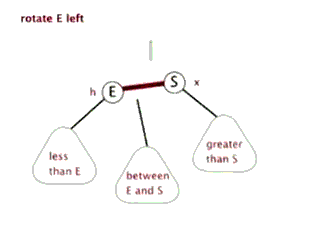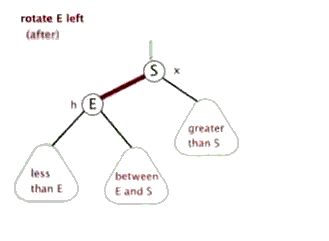
例子讲解

初始状态如下：

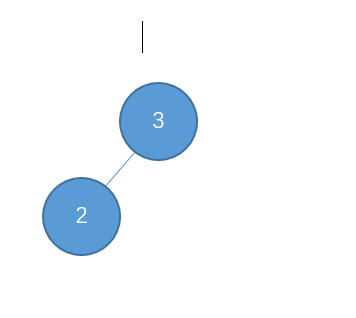
然后我们主键插入如下数值：1,4,5,6,7,10,9,8

插入 1

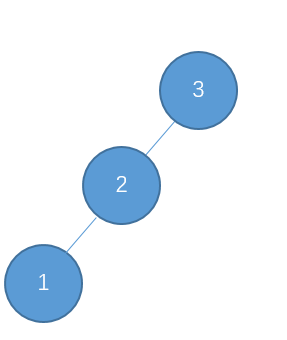
左-左型，需要右旋调整。

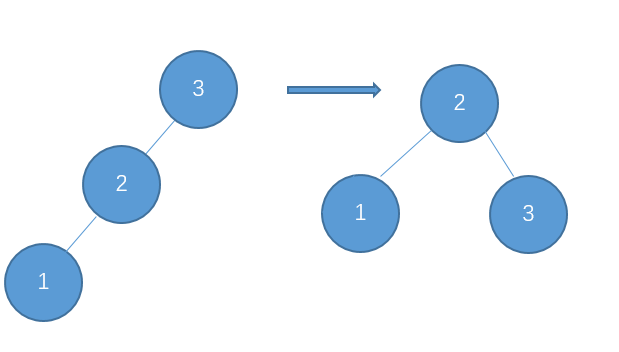
插入4

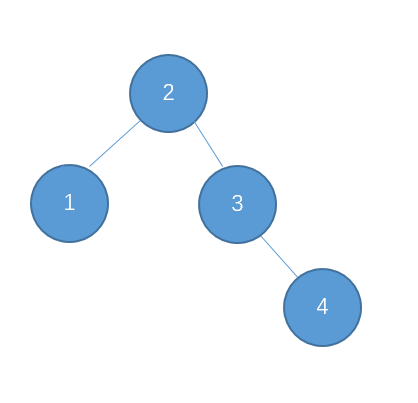
继续插入 5

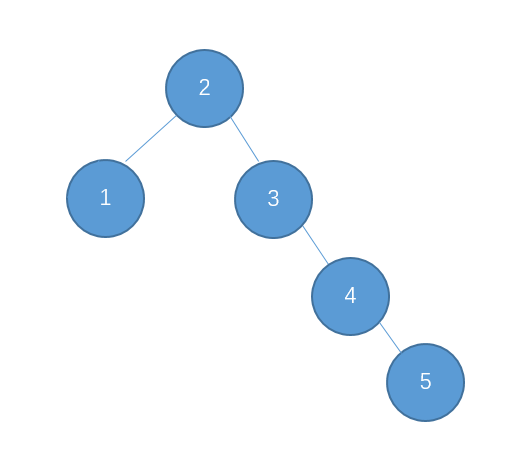
右-右型，需要左旋转调整。

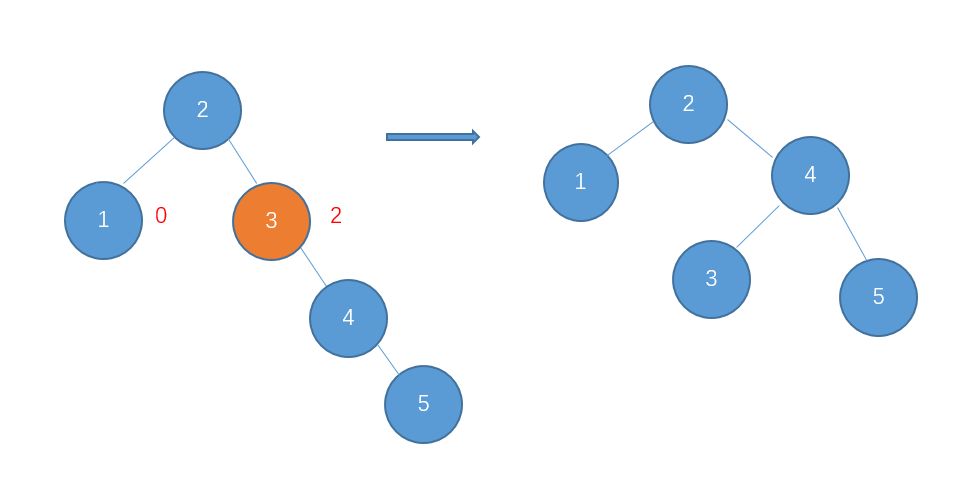
继续插入6

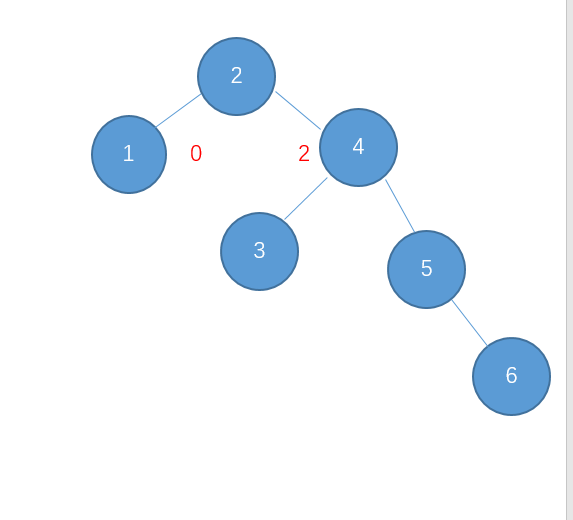
右-右型，需要进行左旋

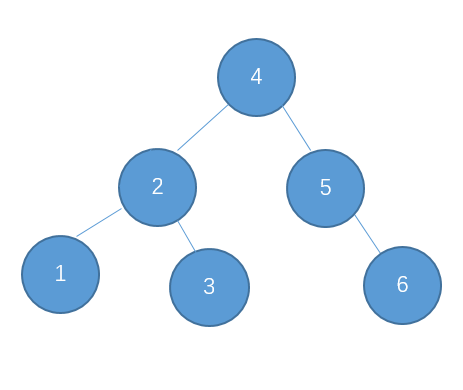
继续插入7

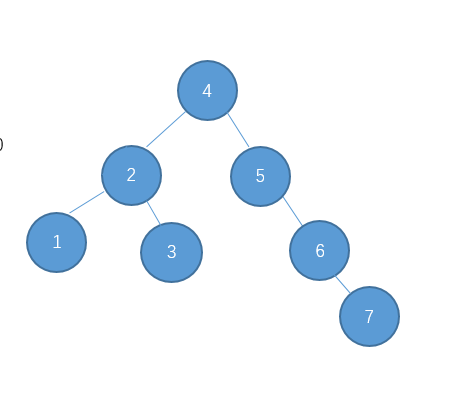
右-右型，需要进行左旋

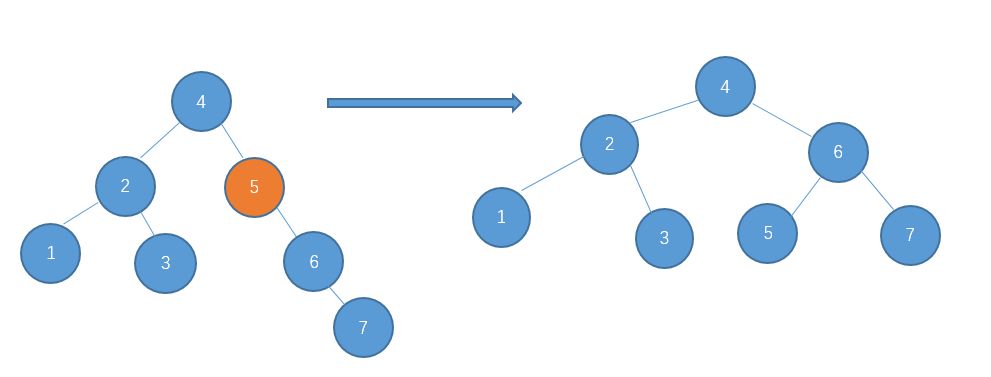
继续插入10

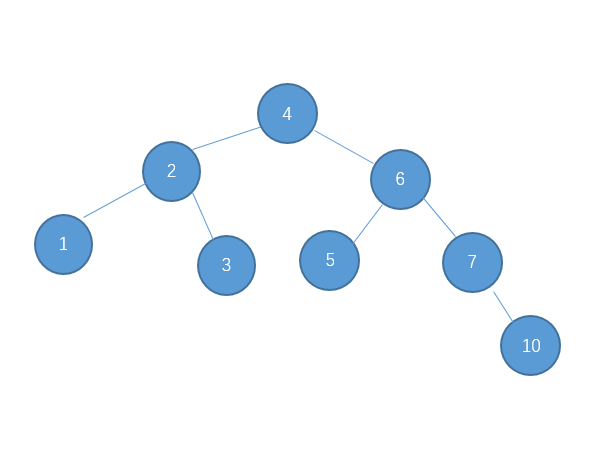
继续插入9

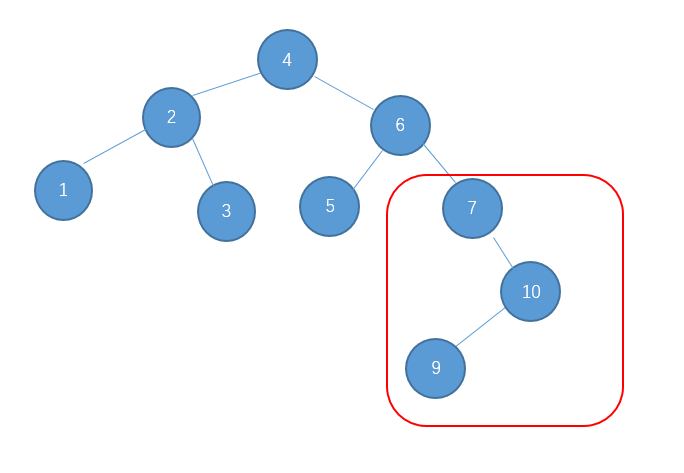
出现了这种情况怎么办呢?对于这种 右-左型的情况，单单一次左旋或右旋是不行的，下面我们先说说如何处理这种情况。

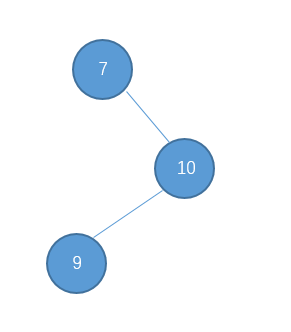
这种我们就把它称之为右-左 型吧。处理的方法是先对节点10进行右旋把它变成右-右型。

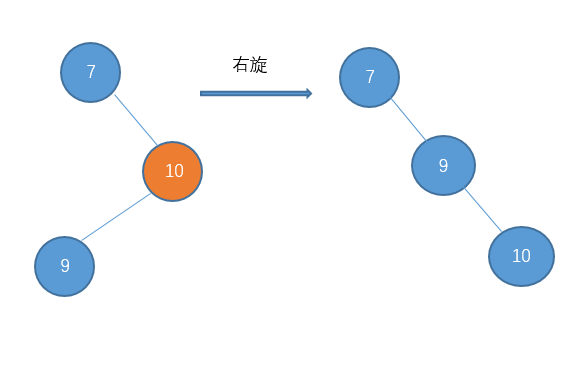
然后在进行左旋。

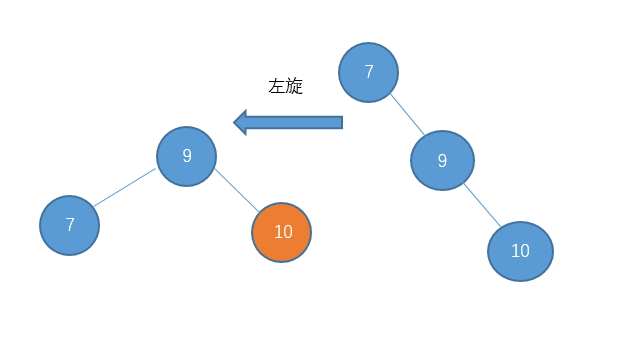
所以对于这种右-左型的，我们需要进行一次右旋再左旋。

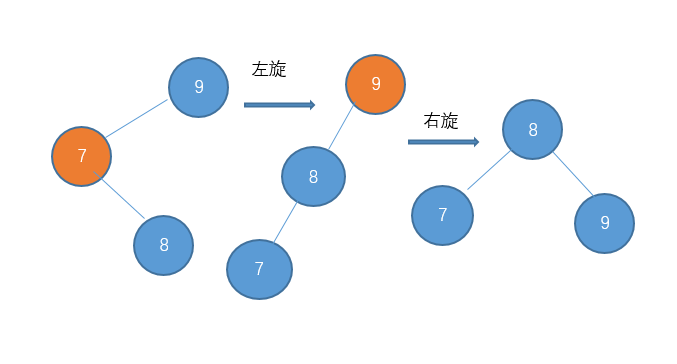
同理，也存在左-右型的，例如：

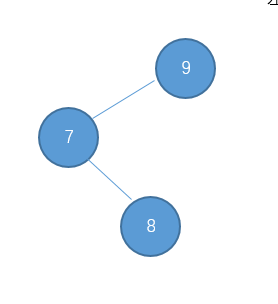
对于左-右型的情况和刚才的 右-左型相反，我们需要对它进行一次左旋，再右旋。

回到刚才那道题

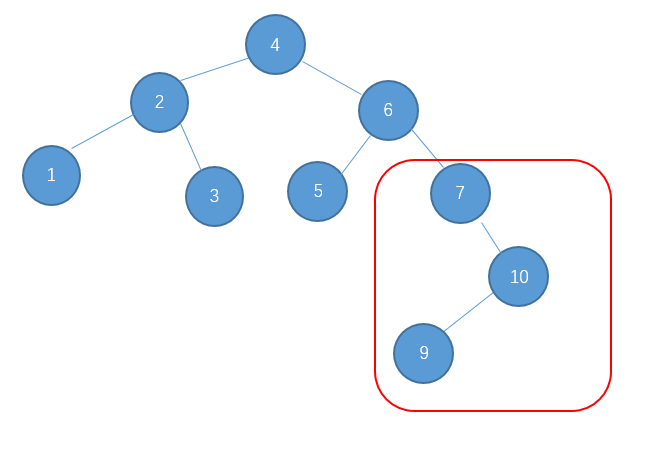
对它进行右旋再左旋。

到此，我们的插入就

总结一下

在插入的过程中，会出现一下四种情况破坏AVL树的特性，我们可采取如下相应的旋转。

1、左-左型：做右旋。

2、右-右型：做左旋转。

3、左-右型：先做左旋，后做右旋。

4、右-左型：先做右旋，再做左旋。

不知道大家发现规律没，这个规则还是挺好记。

代码实现

//定义节点

classAvlNode{

intdata;

AvlNode lchild; //左孩子

AvlNode rchild; //右孩子

intheight; //记录节点的高度

}

//在这里定义各种操作

publicclassAVLTree{

//计算节点的高度

staticintheight(AvlNode T) {

if(T == null) {

return-1;

} else{

returnT.height;

}

}

//左左型，右旋操作

staticAvlNode R_Rotate(AvlNode K2) {

AvlNode K1;

//进行旋转

K1 = K2.lchild;

K2.lchild = K1.rchild;

K1.rchild = K2;

//重新计算节点的高度

K2.height = Math.max(height(K2.lchild), height(K2.rchild)) + 1;

K1.height = Math.max(height(K1.lchild), height(K1.rchild)) + 1;

returnK1;

}

//进行左旋

staticAvlNode L_Rotate(AvlNode K2) {

AvlNode K1;

K1 = K2.rchild;

K2.rchild = K1.lchild;

K1.lchild = K2;

//重新计算高度

K2.height = Math.max(height(K2.lchild), height(K2.rchild)) + 1;

K1.height = Math.max(height(K1.lchild), height(K1.rchild)) + 1;

returnK1;

}

//左-右型，进行右旋，再左旋

staticAvlNode R_L_Rotate(AvlNode K3) {

//先对其孩子进行左旋

K3.lchild = R_Rotate(K3.lchild);

//再进行右旋

returnL_Rotate(K3);

}

//右-左型，先进行左旋，再右旋

staticAvlNode L_R_Rotate(AvlNode K3) {

//先对孩子进行左旋

K3.rchild = L_Rotate(K3.rchild);

//在右旋

returnR_Rotate(K3);

}

//插入数值操作

staticAvlNode insert(intdata, AvlNode T) {

if(T == null) {

T = newAvlNode();

T.data = data;

T.lchild = T.rchild = null;

} elseif(data < T.data) {

//向左孩子递归插入

T.lchild = insert(data, T.lchild);

//进行调整操作

//如果左孩子的高度比右孩子大2

if(height(T.lchild) - height(T.rchild) == 2) {

//左-左型

if(data < T.lchild.data) {

T = R_Rotate(T);

} else{

//左-右型

T = R_L_Rotate(T);

}

}

} elseif(data > T.data) {

T.rchild = insert(data, T.rchild);

//进行调整

//右孩子比左孩子高度大2

if(height(T.rchild) - height(T.lchild) == 2)

//右-右型

if(data > T.rchild.data) {

T = L_Rotate(T);

} else{

T = L_R_Rotate(T);

}

}

//否则，这个节点已经在书上存在了，我们什么也不做

//重新计算T的高度

T.height = Math.max(height(T.lchild), height(T.rchild)) + 1;

returnT;

}

}