核密度估计 Kernel Density Estimation (KDE) MATLAB

对于已经得到的样本集，核密度估计是一种可以求得样本的分布的概率密度函数的方法：

通过选取核函数和合适的带宽，可以得到样本的distribution probability，在这里核函数选取标准正态分布函数，bandwidth通过AMISE规则选取

具体原理及定义：传送门 https://en.wikipedia.org/wiki/Density_estimation

MATLAB 代码实现如下：

 % Kernel Density Estimation
 % 只能处理正半轴密度
 function [t, y_true, tt, y_KDE] = KernelDensityEstimation(x)
 % clear

 % x = px_last;
 % x = px_last_tu;
 %%
 %参数初始化
 Max = round(max(x));           %数据中最大值
 Min = round(min(x));           %数据中最小值
 Ntotal = length(x);     %数据个数
 tt =  : 0.1 : Max;     %精确x轴
 t =  : Max;            %粗略x轴

 y_KDE = zeros( * Max+, );   %核密度估计值
 sum1 = ;                       %求和的中间变量
 %%
 %计算带宽h
 R = /(*sqrt(pi));
 m2 = ;
 h = ;
 % h = (R)^(/) / (m2^(/) * R^(/) * Ntotal^(/));

 %%
 %计算核密度估计
 for i =  : 0.1 : Max
     for j =  : Ntotal
         sum1 = sum1 + normpdf(i-x(j));
     end
     y_KDE(round(i*+)) = sum1 / (h * Ntotal);
     sum1 = ;
 end

 sum2 = sum(y_KDE)*0.1;  %归一化KDE密度
 for i =  : 0.1 : Max
     y_KDE(round(i*+)) = y_KDE(round(i*+))/sum2;
 end

 %%
 %计算真实密度的分布
 y_true = zeros(Max+,);
 for i =  : Max
     for j =  : Ntotal
         if (x(j) < i+)&&(x(j) >= i)
             y_true(i+) = y_true(i+) + ;
         end
     end
     y_true(i+) = y_true(i+) / Ntotal;
 end

 %%
 %绘图

 % figure()           %真实密度的分布图象
 % bar(t, y_true);
 % axis([Min Max+  max(y_true)*1.1]);
 %
 % figure()           %核密度估计的密度分布图象
 % plot(tt, y_KDE);
 % axis([Min Max  max(y_true)*1.1]);

给定测试数据：

data = [1,2,3,4,5,2,1,2,4,2,1,4,7,4,1,2,4,9,8,7,10,1,2,3,1,0,0,3,6,7,8,9,4]

样本的条形统计图和KDE密度分布图分别如下，可以看到KDE可以较好的还原样本的分布情况：

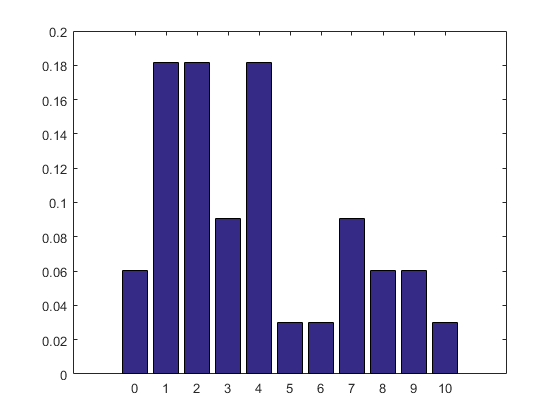
真实概率分布图

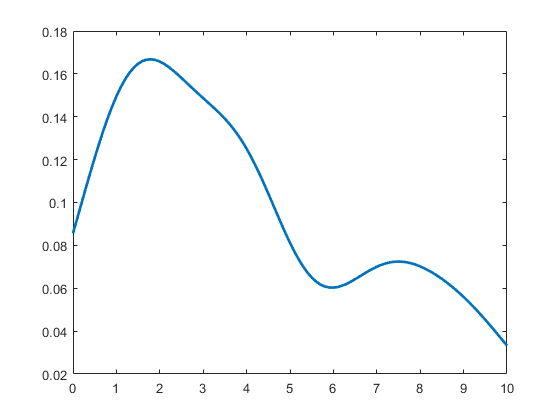
KDE密度分布图