机器学习：SVM（SVM 思想解决回归问题）

一、SVM 思想在解决回归问题上的体现

• 回归问题的本质：找到一条直线或者曲线，最大程度的拟合数据点；
• 怎么定义拟合，是不同回归算法的关键差异；

1. 线性回归定义拟合方式：让所有数据点到直线的 MSE 的值最小；
2. SVM 算法定义拟合的方式：在距离 Margin 的区域内，尽量多的包含样本点；

• SVM 的思路解决回归问题：

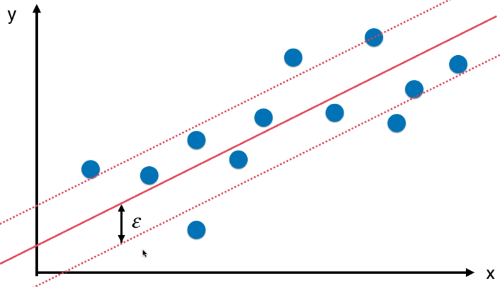
1. 在 Margin 区域内的样本点越多，则 Margin 区域越能够较好的表达样本数据点，此时，取 Margin 区域内中间的那条直线作为最终的模型；用该模型预测相应的样本点的 y 值；
2. 在具体训练 SVM 算法模型解决回归问题时，提前指定 Margin 的大小，算法引入的超参数：ε，表示 Margin 区域的两条直线到区域中间的直线的距离，如图：

• 

• SVM 解决回归问题的思路与解决分类问题的思路相反，解决分类问题时，希望 Margin 区域内没有样本点或者样本点尽可能的少；

• LinearSVC、SVC、LinearSVR、SVR ：

1. LinearSVC：使用线性 SVM 的思路解决分类问题；
2. SVC：使用非线性 SVM 的思路解决分类问题；（多项式核、高斯核）
3. LinearSVR：使用线性 SVM 的思路解决回归问题；
4. SVR：使用非线性 SVM 的思路解决回归问题；（使用不同的核函数）

二、scikit-learn 中的 SVM 算法：LinearSVR、SVR 解决回归问题

• LinearSVR、SVR 的使用方式与 LinearSVC、SVC 一样

• import numpy as np
  import matplotlib.pyplot as plt
  from sklearn import datasets
  
  boston = datasets.load_boston()
  X = boston.data
  y = boston.target
  
  from sklearn.model_selection import train_test_split
  X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
  
  from sklearn.svm import LinearSVR
  from sklearn.svm import SVR
  from sklearn.preprocessing import StandardScaler
  from sklearn.pipeline import Pipeline
  
  def StandardLinearSVR(epsilon=0.1):
      return Pipeline([
          ('std_scaler', StandardScaler()),
          ('linearSVR', LinearSVR(epsilon=epsilon))
          # 此处使用超参数 C 的默认值;
          # 如果使用 SVR()，还需要调节参数 kernel；
      ])
  
  svr = StandardLinearSVR()
  svr.fit(X_train, y_train)
  svr.score(X_test, y_test)
  # 准确率：0.6353520110647206