POJ3352 Road Construction (双连通分量)

Road Construction

Time Limit:2000MS    Memory Limit:65536KB    64bit IO Format:%I64d
& %I64u

SubmitStatus

Description

It's almost summer time, and that means that it's almost summer construction time! This year, the good people who are in charge of the roads on the tropical island paradise of Remote Island would like to repair and upgrade the various roads that lead between
the various tourist attractions on the island.

The roads themselves are also rather interesting. Due to the strange customs of the island, the roads are arranged so that they never meet at intersections, but rather pass over or under each other using bridges and tunnels. In this way, each road runs between
two specific tourist attractions, so that the tourists do not become irreparably lost.

Unfortunately, given the nature of the repairs and upgrades needed on each road, when the construction company works on a particular road, it is unusable in either direction. This could cause a problem if it becomes impossible to travel between two tourist
attractions, even if the construction company works on only one road at any particular time.

So, the Road Department of Remote Island has decided to call upon your consulting services to help remedy this problem. It has been decided that new roads will have to be built between the various attractions in such a way that in the final configuration,
if any one road is undergoing construction, it would still be possible to travel between any two tourist attractions using the remaining roads. Your task is to find the minimum number of new roads necessary.

Input

The first line of input will consist of positive integers n and r, separated by a space, where 3 ≤n ≤ 1000 is the number of tourist attractions on the island, and 2 ≤r ≤ 1000 is the number of roads. The tourist attractions
are conveniently labelled from 1 ton. Each of the followingr lines will consist of two integers,v andw, separated by a space, indicating that a road exists between the attractions labelledv andw. Note that
you may travel in either direction down each road, and any pair of tourist attractions will have at most one road directly between them. Also, you are assured that in the current configuration, it is possible to travel between any two tourist attractions.

Output

One line, consisting of an integer, which gives the minimum number of roads that we need to add.

Sample Input

Sample Input 1
10 12
1 2
1 3
1 4
2 5
2 6
5 6
3 7
3 8
7 8
4 9
4 10
9 10

Sample Input 2
3 3
1 2
2 3
1 3

Sample Output

Output for Sample Input 1
2

Output for Sample Input 2
0

解题链接：http://blog.csdn.net/lyy289065406/article/details/6762370

大致题意：

某个企业想把一个热带天堂岛变成旅游胜地，岛上有N个旅游景点，任意2个旅游景点之间有路径连通（注意不一定是直接连通）。而为了给游客提供更方便的服务，该企业要求道路部门在某些道路增加一些设施。

道路部门每次只会选择一条道路施工，在该条道路施工完毕前，其他道路依然可以通行。然而有道路部门正在施工的道路，在施工完毕前是禁止游客通行的。这就导致了在施工期间游客可能无法到达一些景点。

为了在施工期间所有旅游景点依然能够正常对游客开放，该企业决定搭建一些临时桥梁，使得不管道路部门选在哪条路进行施工，游客都能够到达所有旅游景点。给出当下允许通行的R条道路，问该企业至少再搭建几条临时桥梁，才能使得游客无视道路部门的存在到达所有旅游景点？

解题思路：

做过POJ2942后，这题根本就是水题嘛= =

首先建立模型：

给定一个连通的无向图G，至少要添加几条边，才能使其变为双连通图。

模型很简单，正在施工的道路我们可以认为那条边被删除了。那么一个图G能够在删除任意一条边后，仍然是连通的，当且仅当图G至少为双连通的。

PS：不要问我为什么不是3-连通、4-连通...人家题目问“至少添加几条边”好不...

显然，当图G存在桥（割边）的时候，它必定不是双连通的。桥的两个端点必定分别属于图G的两个【边双连通分量】（注意不是点双连通分量），一旦删除了桥，这两个【边双连通分量】必定断开，图G就不连通了。但是如果在两个【边双连通分量】之间再添加一条边，桥就不再是桥了，这两个【边双连通分量】之间也就是双连通了。

那么如果图G有多个【边双连通分量】呢？至少应该添加多少条边，才能使得任意两个【边双连通分量】之间都是双连通（也就是图G是双连通的）？

这个问题就是本题的问题。要解决这个问题：

1、  首先要找出图G的所有【边双连通分量】。

Tarjan算法用来寻找图G的所有【边双连通分量】是最简单有效的方法，因为Tarjan算法在DFS过程中会对图G所有的结点都生成一个Low值，而由于题目已表明任意两个结点之间不会出现重边，因此Low值相同的两个结点必定在同一个【边双连通分量】中！  （如果是有重边的话，那么不同的low值是可能是属于同一个边双连通分量的，这个时候就要通过其他方法去求解边双连通分量。不过这不是本题要讨论的）

2、  把每一个【边双连通分量】都看做一个点（即【缩点】）

也有人称【缩点】为【块】，都是一样的。其实缩点不是真的缩点，只要利用Low值对图G的点分类处理，就已经缩点了。

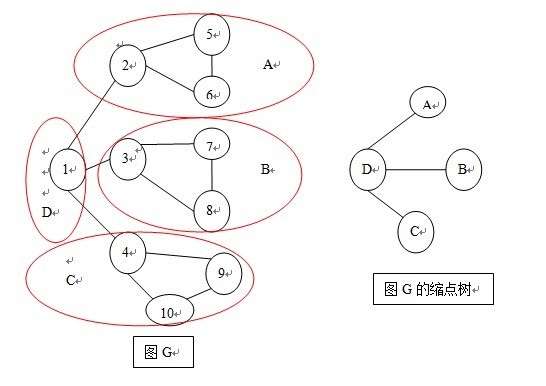
以样例1为例，样例1得到的图G为上左图，

其中Low[4]=Low[9]=Low[10]

Low[3]=Low[7]=Low[8]

Low[2]=Low[5]=Low[6]

Low[1]独自为政....

把Low值相同的点划分为一类，每一类就是一个【边双连通分量】，也就是【缩点】了，不难发现，连接【缩点】之间的边，都是图G的桥，那么我们就得到了上右图以缩点为结点，已桥为树边所构造成的树。

3、  问题再次被转化为“至少在缩点树上增加多少条树边，使得这棵树变为一个双连通图”。

首先知道一条等式：

若要使得任意一棵树，在增加若干条边后，变成一个双连通图，那么

至少增加的边数 =（ 这棵树总度数为1的结点数 + 1 ）/ 2

（证明就不证明了，自己画几棵树比划一下就知道了）

那么我们只需求缩点树中总度数为1的结点数（即叶子数）有多少就可以了。换而言之，我们只需求出所有缩点的度数，然后判断度数为1的缩点有几个，问题就解决了。

4、  求出所有缩点的度数的方法

两两枚举图G的直接连通的点，只要这两个点不在同一个【缩点】中，那么它们各自所在的【缩点】的度数都+1。注意由于图G时无向图，这样做会使得所有【缩点】的度数都是真实度数的2倍，必须除2后再判断叶子。

图论基本概念：http://blog.csdn.net/u014665013/article/details/50009399

相似题目：POJ 3177

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define MOD 100000
#define inf 1<<29
#define LL long long
#define MAXN 20010
#define MAXM = 50010
using namespace std;
struct Edge
{
    int to,next;
    bool cut;
} edge[MAXN];
int head[MAXN],tot;
int low[MAXN],DFN[MAXN],belong[MAXN];///belong 的值为1-block
int index,top;
int block ;  ///强连通分量
bool inStack[MAXN];
int bridgeNum;  ///桥的数目
int stack[MAXN]; 

void addedge(int u,int v)
{
    edge[tot].to = v;
    edge[tot].next = head[u];
    edge[tot].cut = false;
    head[u] = tot++ ;
}

void Tarjan(int u,int pre)
{
    int v;
    low[u] = DFN[u] = ++index;
    stack[top++] = u;
    inStack[u] = true;
    for(int i=head[u] ; i!=-1 ; i=edge[i].next)
    {
        v = edge[i].to;
        if( v == pre ) continue;    ///因为是无向图，所以两条是双向的，所以只遍历一条就够了
        if( !DFN[v] )
        {
            Tarjan(v,u);
            if(low[u]>low[v])
                low[u] = low[v];
            if(low[v] > DFN[u] ){  ///尽量不要这么用
                bridgeNum++;
                edge[i].cut = true;
                edge[i^1].cut = true;  ///将两条双向边都设置为桥
            }
        }
        else if( inStack[v] && low[u] > DFN[v])
            low[u] = DFN[v];
    }
    if(low[u] == DFN[u])
    {
        block++;
        do
        {
            v=stack[--top];  ///清空当前强连通分量栈 必须清空
            inStack[v] = false;
            belong[v]=block;   ///v节点都编号为block  也就是这是一个块
        }
        while(v!=u);

    }
}
int du[MAXN] ;

void solve(int N)
{
    memset(DFN,0,sizeof(DFN));
    memset(inStack,false,sizeof(inStack));
    index = block = top =0;
    Tarjan(1,0);
    int ans = 0;
    memset(du,0,sizeof(du));
    for(int i=1; i<=N ; i++)  ///缩点
        for(int j=head[i] ; j!=-1 ; j=edge[j].next)
          if( edge[j].cut )
              du[ belong[i] ]++;
    for(int i=1;i<block ;i++)
        if(du[i] == 1)  ///叶子节点
           ans++;
    printf("%d\n",(ans+1)/2 );
}
void init()
{
    tot =  0;
    memset(head,-1,sizeof(head));
}

int main ()
{
    int n,m;
    while(~scanf("%d%d",&n,&m))
    {
        int u,v;
        init();
        for(int i=0; i<m; i++)
        {
            scanf("%d%d",&u,&v);
            addedge(u,v);
            addedge(v,u);
        }
        solve(n);
    }
    return 0;
}

这个代码比较简洁。。。没有求桥，没用辅助数组belong

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<queue>
#define M 1007
using namespace std;
int dfn[M],low[M],head[M],vis[M],stack[M],belong[M];
int n,m,cnt,scnt,begin,num;
int g[M][M],in[M];
struct E
{
    int v,to;
}edg[M*M];
void init()
{
    memset(head,-1,sizeof(head));
    memset(dfn,0,sizeof(dfn));
    memset(low,0,sizeof(low));
    memset(in,0,sizeof(in));
    cnt=scnt=num=begin=0;
}
void addedge(int u,int v)
{
    edg[num].v=v;edg[num].to=head[u];
    head[u]=num++;
}
void tarjan(int x,int y)
{
    int v;
    dfn[x]=low[x]=++cnt;
    for(int i=head[x];i!=-1;i=edg[i].to)
    {
        v=edg[i].v;
        if(v==y)continue;
        if(!dfn[v])
            tarjan(v,x);
        low[x]=min(low[x],low[v]);
    }
}
int main()
{
        init();
        scanf("%d%d",&n,&m);
        int a,b;
        for(int i=0;i<m;i++)
        {
            scanf("%d%d",&a,&b);
            addedge(a,b);
            addedge(b,a);
        }
        tarjan(1,1);
        for(int u=1;u<=n;u++)
            for(int j=head[u];j!=-1;j=edg[j].to)
            {
                int v=edg[j].v;
                if(low[u]!=low[v])
                    in[low[u]]++;
            }
        int ans=1;
        for(int i=1;i<=n;i++)
            if(in[i]==1)ans++;
        printf("%d\n",ans/2);
    return 0;
}