[HNOI2009]双递增序列(洛谷P4728)+小烈送菜(内部训练题)——奇妙的dp
博主学习本题的经过嘤嘤嘤:
7.22 : 听学长讲(一知半解)——自己推(推不出来)——网上看题解——以为自己会了(网上题解是错的)——发现错误以后又自己推(没推出来)——给学长发邮件——得到正确解法——按着学长思路又推一遍——最后理解
(前后的“学长”不是同一个人)
7.23 : 写出代码,完善细节。
(建议改成:西 天 取 经)
首先,网上对于这道题的题解绝大部分是错误的!(比如洛谷上的部分题解)
用LIS做是不行的
玄学贪心是不行的
dp转移方程不能自圆其说是不行的
即使是AC代码也不一定是正确的(2009年的省选,数据太太太太太太太太太太太太太太水了嘤嘤嘤)
废话说完了
~~~~~~~~~~~~~~~嘤嘤嘤来自蒟蒻OIerOrzer的分割线啦嘤嘤嘤~~~~~~~~~~~~~~~~
以下为正文部分嘤嘤嘤:
考虑把一个数列分成两个集合,有a[i]的为一个集合,没有a[i]的为一个集合~
我们定义状态转移方程dp[i][j]表示对于前i个数,有a[i]的集合的长度为j,没有a[i]的集合的最后一个数的最小值为dp[i][j](神仙定义)
也就是说,现在有两个集合,其中一个有a[i],另一个没有a[i]。尝试把a[i+1]放到其中一个集合中。
1.尝试把a[i+1]放到有a[i]的集合当中。那么需要满足的先决条件就是:a[i+1]>a[i].
此时更新dp[i+1][j+1](因为把a[i]放到长度为j的集合中,于是长度++)此时没有a[i+1]的集合同时也是没有a[i]的集合,换句话来说,这个转移对没有a[i]的集合是没有改变的,所以,dp[i+1][j+1]可以直接由dp[i][j]继承过来。
2.尝试把a[i+1]放到没有a[i]的集合当中。那么需要满足的先决条件就是:a[i+1]>dp[i][j].
此时更新dp[i+1][i-j+1](原来没有a[i]的集合的长度为(i-j),把a[i+1]放进去,长度++)既然把a[i+1]放到了没有a[i]的集合中,那么,没有a[i+1]的集合的最后一个数就是a[i],于是,用a[i]去更新dp[i+1][i-j+1];
(真绕啊嘤嘤嘤)
上代码嘤嘤嘤:
1 #include <bits/stdc++.h>
2 using namespace std;
3 const int maxn=2000+10;
4 int dp[maxn][maxn],a[maxn];
5 int n,m;
6 void Solve(){
7 scanf("%d",&m);
8 while(m--){
9 scanf("%d",&n);
10 memset(dp,0x3f,sizeof(dp));
11 memset(a,0x3f,sizeof(a));
12 for(int i=1;i<=n;++i) scanf("%d",&a[i]);
13 dp[1][1]=-1;//因为数据中可能有0,因此不能初始化为0;
14 for(int i=1;i<=n;++i){
15 for(int j=1;j<=i;++j){
16 if(a[i+1]>a[i]) dp[i+1][j+1]=min(dp[i+1][j+1],dp[i][j]);
17 if(a[i+1]>dp[i][j]) dp[i+1][i-j+1]=min(dp[i+1][i-j+1],a[i]);
18 }
19 }
20 if(dp[n][n/2]>1e8) printf("No!\n");
21 //没有更新,说明不能将原序列合法地平分成两部分,就输出No;
22 else printf("Yes!\n");
23 }
24 }
25 int main(){
26 Solve();
27 return 0;
28 }
完结撒花嘤嘤嘤~(然而并没有)

上辈子的题了(大雾)(所以这就是火星水吗)
但是在解决上一道题后会发现对于这道题会有不一样的理解~~~
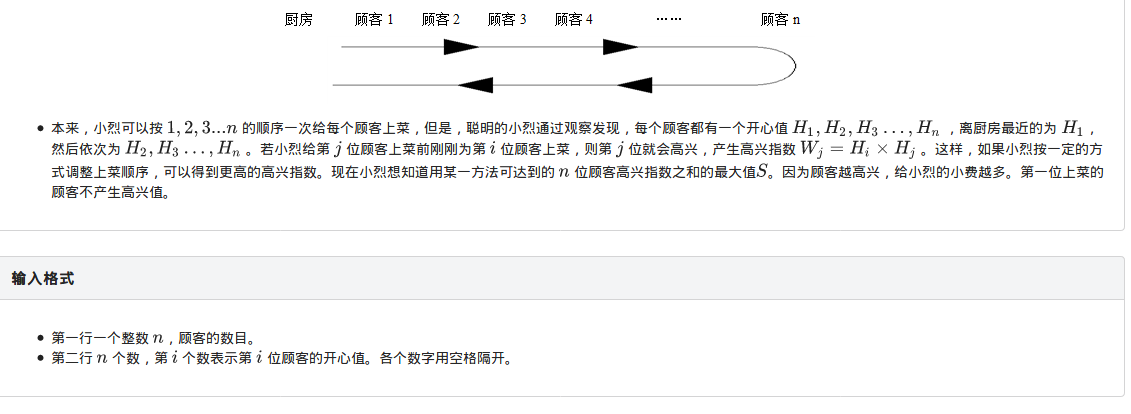
我们先定义dp[i][j]表示小烈1走到i,小烈2走到j时的最大收益。且默认小烈1始终在小烈2前面,且前j个已经被送完。
换句话来说,其实根本没有小烈1和小烈2(只是我们yy出来的)或者说,并不是划分了“小烈1”和“小烈2”这两个抽象的概念,划分的应该是“送了a[i]的小烈”和“没有送a[i]的小烈”!
(woc这不就是上一道题吗,太像了好叭)
现在我们换一种表达方式来定义dp[i][j]:
dp[i][j]表示前i个客人,没有送过a[i]的小烈最后一个送的是a[j]时的最大收益。
默认j小于i,且前j个一定已经送过了(如果前j个有没有送过的,那就不合法了,因为两个小烈不能回头)
现在考虑a[i+1]由谁送。
1.由送了a[i]的小烈送。所以,没有送a[i]的小烈同样没有送a[i+1]。也就是说,这个转移完成后,没有送a[i]的小烈原来在j,现在还是在j,没有变化。
所以用(dp[i][j]+a[i]*a[i+1])更新(dp[i+1][j])。
2.由没有送a[i]的小烈送。所以,送了a[i]的小烈没有送a[i+1]。也就是说,没有送a[i+1]的小烈最后一个送的是a[i]!
所以用(dp[i][j]+a[j]*a[i+1])更新(dp[i+1][i]).
(和刚才那个一样绕嘤嘤嘤)
上代码:


1 #include <bits/stdc++.h>
2 using namespace std;
3 const int maxn=2500+10;
4 int dp[maxn][maxn],a[maxn],ans;
5 void Solve(){
6 int n;scanf("%d",&n);
7 for(int i=1;i<=n;++i) scanf("%d",&a[i]);
8 for(int i=1;i<=n;++i){
9 for(int j=0;j<i;++j){//j的范围要搞清楚哦;
10 dp[i+1][j]=max(dp[i+1][j],dp[i][j]+a[i]*a[i+1]);
11 dp[i+1][i]=max(dp[i+1][i],dp[i][j]+a[j]*a[i+1]);
12 }
13 }
14 for(int i=0;i<n;++i) ans=max(ans,dp[n][i]+a[i]*a[n]);
15 /*现实中的小烈是从1走到n,又从n回去,在dp方程里面我们把一个小烈拆成了两个,
16 其中一个表示现实中正向走的部分,另一个表示现实中反向走的部分(但是令这一个
17 反向走的小烈反过来走,就是正着走)也就是说,当现实中小烈走到n,开始返回的
18 时候,a[n]与dp方程中定义的小烈2经过的最后一个a[i](也就是反着走的第一个
19 a[i])是要产生一个值的,而这个值要加到答案里面才能得到最终结果*/
20 printf("%d",ans);
21 }
22 int main(){
23 Solve();
24 return 0;
25 }
嘤嘤嘤
完结撒花花!!!
[HNOI2009]双递增序列(洛谷P4728)+小烈送菜(内部训练题)——奇妙的dp的更多相关文章
- 【BZOJ1489】[HNOI2009]双递增序列(动态规划)
[BZOJ1489][HNOI2009]双递增序列(动态规划) 题面 BZOJ 洛谷 题解 这\(dp\)奇奇怪怪的,设\(f[i][j]\)表示前\(i\)个数中,第一个数列选了\(j\)个数,第二 ...
- 小烈送菜——奇怪的dp
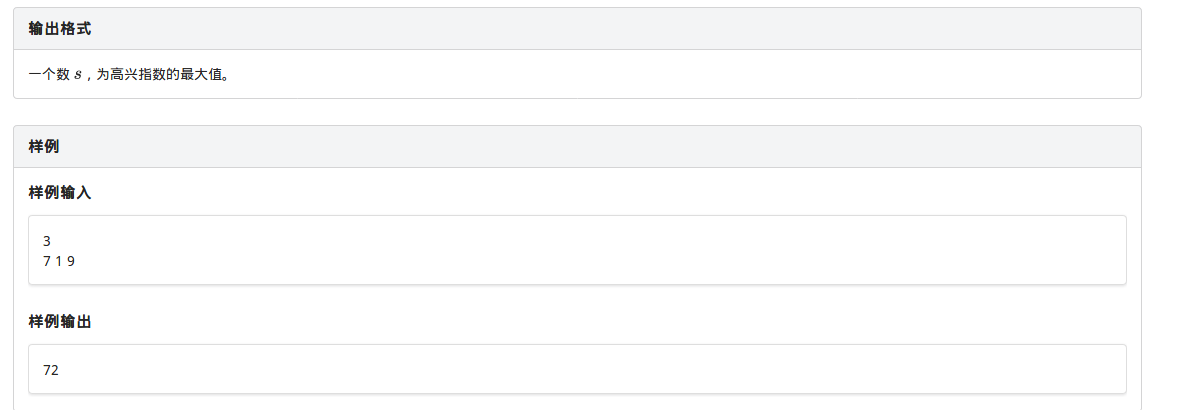
小烈送菜 题目描述 小烈一下碰碰车就被乐满地的工作人员抓住了.作为扰乱秩序的惩罚,小烈必须去乐满地里的"漓江村"饭店端盘子. 服务员的工作很繁忙.他们要上菜,同时要使顾客们尽量高兴 ...
- 线性DP之小烈送菜
小烈送菜 小烈一下碰碰车就被乐满地的工作人员抓住了.作为扰乱秩序的惩罚,小烈必须去乐满地里的"漓江村"饭店端盘子. 服务员的工作很繁忙.他们要上菜,同时要使顾客们尽量高兴.一位服务 ...
- 方格取数(简单版)+小烈送菜(不知道哪来的题)-----------奇怪的dp增加了!
一.方格取数: 设有N*N的方格图(N<=20),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字0. 某人从图的左上角的A(1,1) 点出发,可以向下行走,也可以向右走,直到到达右下 ...
- 【题解】洛谷P1373 小a和uim之大逃离(坐标DP)
次元传送门:洛谷P1373 思路 设f[i][j][t][1/0]表示走到(i,j)时 小a减去uim的差值为t 当前是小a取(0) uim取(1) 那么转移就很明显了 f[i][j][t][]=(f ...
- P4728 [HNOI2009]双递增序列
题意 这个DP状态有点神. 首先考虑一个最暴力的状态:\(f_{i,j,k,u}\)表示第一个选了\(i\)个,第二个选了\(j\)个,第一个结尾为\(k\),第二个结尾为\(u\)是否可行. 现在考 ...
- [luogu4728 HNOI2009] 双递增序列 (dp)
传送门 Solution 前几天刚做了类似题,这种将一个序列拆分为两个单调序列的题一般都是设\(dp[i]\)表示i为一个单调序列的末尾时,另一个序列的末尾是多少 然后应用贪心的思想,在这道题中就是让 ...
- [HNOI2009]双递增序列(动态规划,序列dp)
感觉这个题还蛮难想的. 首先状态特别难想.设\(dp[i][j]\)表示前i个数,2序列的长度为j的情况下,2序列的最后一个数的最小值. 其中1序列为上一个数所在的序列,2序列为另外一个序列. 这样设 ...
- [HNOI2009]双递增序列
不难发现本题贪心是不好做的,可以考虑 \(dp\). 首先的一个想法就是令 \(dp_{i, j, k, l}\) 表示当前选到第 \(i\) 个位置,当前第一个序列选了 \(j\) 个数,当前第一个 ...
随机推荐
- JS009. 数组去重的多种方法总结与一步步优化
两层for循环 这种函数的优点是兼容性好比较通用,缺点是时空复杂度都很直观的为O(n2),不利于维护和性能. var array = [1,1,'1','1'] function unique(arr ...
- Object类、Date类、Calendar类、System类、StringBuilder类和基本类型包装类
一.Object类--toString方法 1.普通类重写toString方法,不然打印出来是存在栈内存的对象引用名称的堆内存中该对象的地址值: 2.equals方法: String比较equals是 ...
- 使用Redis Stream来做消息队列和在Asp.Net Core中的实现
写在前面 我一直以来使用redis的时候,很多低烈度需求(并发要求不是很高)需要用到消息队列的时候,在项目本身已经使用了Redis的情况下都想直接用Redis来做消息队列,而不想引入新的服务,kafk ...
- Shell系列(37)- while和until循环
while循环 只要条件判断式成立则进行循环,并执行循环程序:一旦循环条件不成立,则终止循环 格式 while [ 条件判断式 ] do 程序 done 例子 需求:计算工具,1+2+--100的和 ...
- python学习笔记(六)-集合
集合是一个无序不重复元素的集.基本功能包括关系测试和消除重复元素.集合对象还支持union(联合),intersection(交),difference(差)和sysmmetric differenc ...
- Css3 3D 旋转动画效果
需求: 1.一个列表滑动效果为360 旋转 准备: 1.css 基础 2.Css 动画基础animation 3.transform-style概念 4 transform 概念 5 JavaScri ...
- 完美解决JavaIO流报错 java.io.FileNotFoundException: F:\ (系统找不到指定的路径。)
完美解决JavaIO流报错 java.io.FileNotFoundException: F:\ (系统找不到指定的路径.) 错误原因 读出文件的路径需要有被拷贝的文件名,否则无法解析地址 源代码(用 ...
- 鸿蒙内核源码分析(信号消费篇) | 谁让CPU连续四次换栈运行 | 百篇博客分析OpenHarmony源码 | v49.04
百篇博客系列篇.本篇为: v49.xx 鸿蒙内核源码分析(信号消费篇) | 谁让CPU连续四次换栈运行 | 51.c.h .o 进程管理相关篇为: v02.xx 鸿蒙内核源码分析(进程管理篇) | 谁 ...
- Winfrom 中完美设置webbrowser控件内核版本
前言 .NET 版本更新了一代又一代,winform中的webbrowser控件的IE内核版本却始终用的IE7,好多网站都对IE7已经不支持.webbrowser这个控件就显得有些鸡肋,经过查找大佬门 ...
- 图神经网络(GNN)--slide
课件是学习小组汇报时用的,许多资料是从大佬哪里搬运的.Tex文档也在里面. GNN课件,下载不了,可以点击 带你入门图神经网络(GNN) 图神经网络(GNN)学习推荐网址 傅里叶分析之掐死教程(完整版 ...
