hdu3313 最大流找关键点,或者最短路找关键点.

题意:

     给你一个有向图,然后给你起点和终点,问你从起点到终点有多少个关键点,如果当前的这个点删除了就无法从起点到终点,那么这个点就是一个关键点..

思路:

     (1)有两种做法,我用的是最大流的,另一种是先跑最短路然后搜索,先说最大流,最大流的很容易理解,首先我们拆点建图,每个点拆成两个点,限流是1,然后起点和终点的限流是2,点于点之间是INF,跑一遍最大流,如果流量是0,说明不连接,那么所有的点都是关键点,输出n,如果流量是2那么说明最小割是2,也就是说无论你把那个点删除都不影响连通性,所以只有起点和终点是关键点,如果流量是1,那也就是说在路途中可能存在关键点,那么我们就

用暴力搜索的方式去找这些关键点,对于搜索这块我自己卡了两天了,今天才弄明白,首先我们定义跑完最大流后流量为0的边为关键边,首先第一个点一定是关键点,我们一个一个找,我的理解是 从当前的这个关键点出发,通过非关键边搜索,第一个搜索不到的点一定是关键点,这里的搜索不到的点指的是我们比如当前边u,v,他沿着非关键边无法从u走到v,但是沿着关键边可以走到,那么v就是第一个搜不到的点,v一定是关键点,跑完最大流后,流量0(正向)的是关键路径上的点,非0的是非关键路径上的点,我们每次从当前的关键点出发,沿着流量非0的跑,把这次跑到的点全记录下来,mark上,然后枚举每一个搜到的点相邻的点,如果是流量0,那么这个就是第一个到达不了的点,那么他一定是关键点,这届break,以这个点为起点在接着搜索,就这样一直找到T为止.还有为什么上面有两条边是2而不是别的,是为了缩短时间,2最多两次,我们是为了找到答案是0,1,还是其他,2.3.4..都是其他,都是只存在两个关键点的,所以我们要节省时间,流量2,如果弄大了答案肯定对,但会TLE...

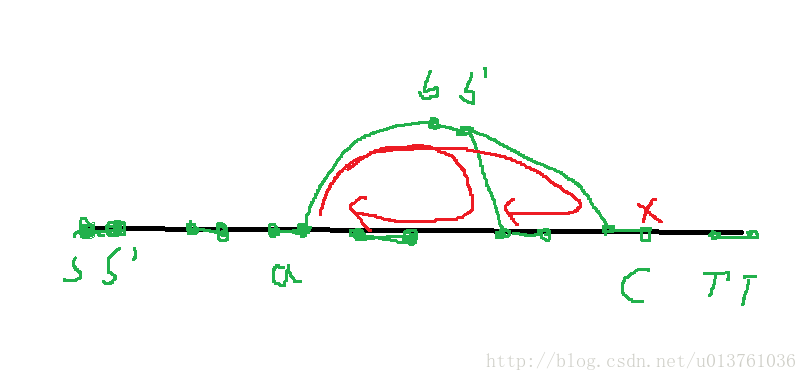
最大流已知当前点找下一个关键点的搜索过程,红色是搜索路径,当前点a,下一个关键点是c,

则如图:

#pragma comment(linker, "/STACK:1024000000,1024000000")

#include<stdio.h>
#include<string.h>
#include<queue>

#define N_node 200000 + 20
#define N_edge 600000 + 60
#define INF 1000000000

using namespace std;

typedef struct
{
   int to ,cost ,next;
}STAR;

typedef struct
{
   int x ,t;
}DEP;

STAR E[N_edge];
DEP xin ,tou;
int list[N_node] ,tot;
int deep[N_node] ,list2[N_node];
int mark[N_node] ,num[N_node] ,tt;

void add(int a, int b ,int c)
{
   E[++tot].to = b;
   E[tot].cost = c;
   E[tot].next = list[a];
   list[a] = tot;

   E[++tot].to = a;
   E[tot].cost = 0;
   E[tot].next = list[b];
   list[b] = tot;
}

int minn(int x ,int y)
{
   return x < y ? x : y;
}

bool BFS(int s ,int t ,int n)
{
   memset(deep ,255 ,sizeof(deep));
   deep[s] = 0;
   xin.x = s;
   xin.t = 0;
   queue<DEP>q;
   q.push(xin);
   while(!q.empty())
   {
      tou = q.front();
      q.pop();
      for(int k = list[tou.x] ;k ;k = E[k].next)
      {
         xin.x = E[k].to;
         xin.t = tou.t + 1;
         if(deep[xin.x] != -1 || !E[k].cost)
         continue;
         deep[xin.x] = xin.t;
         q.push(xin);
      }
   }
   for(int i = 0 ;i <= n ;i ++)
   list2[i] = list[i];
   return deep[t] != -1;
}

int DFS_FLOW(int s ,int t ,int flow)
{
   if(s == t) return flow;
   int nowflow = 0;
   for(int k = list2[s] ;k; k = E[k].next)
   {
      list2[s] = k;
      int to = E[k].to;
      int cost = E[k].cost;
      if(deep[to] != deep[s] + 1 || !cost) continue;
      int tmp = DFS_FLOW(to ,t ,minn(cost ,flow - nowflow));
      nowflow += tmp;
      E[k].cost -= tmp;
      E[k^1].cost += tmp;
      if(flow == nowflow)
      break;
   }
   if(!nowflow) list2[s] = 0;
   return nowflow;
}

int DINIC(int s ,int t ,int n)
{
   int sum = 0;
   while(BFS(s ,t ,n))
   {
      sum += DFS_FLOW(s ,t ,INF);
   }
   return sum;
}

void dfs(int s)
{
   mark[s] = 1;
   num[++tt] = s;
   for(int k = list[s] ;k ;k = E[k].next)
   {
      int to = E[k].to;
      if(E[k].cost && !mark[to])
      dfs(to);
   }
}

int find(int n ,int S ,int T)
{
   E[list[S]].cost = 0;
   E[list[T - n]].cost= 0;
   int cout = 0;
   memset(mark ,0 ,sizeof(mark));

   while(1)
   {
      tt = 0;
      dfs(S);
      int ok = 1;
      for(int i = 1 ;i <= tt && ok ;i ++)
      {
         for(int k = list[num[i]] ;k && ok ;k = E[k].next)
         if(k % 2 == 0 && !mark[E[k].to] && !E[k].cost)
         {
            ok = 0;
            S = E[k].to;
            cout ++;
            if(E[k].to == T)
            return cout;
         }
      }
   }
}

int main ()
{
   int n ,m ,S ,T ,i ,j ,a ,b ,c;
   while(~scanf("%d %d" ,&n ,&m))
   {
      memset(list ,0 ,sizeof(list));
      tot = 1;
      for(i = 1 ;i <= m ;i ++)
      {
         scanf("%d %d" ,&a ,&b);
         add(a + n + 1,b + 1, INF);
      }
      scanf("%d %d" ,&S ,&T);
      S ++ ,T ++;
      for(i = 1 ;i <= n ;i ++)
      {
         if(i != S && i != T)
         add(i ,i + n ,1);
         else add(i ,i + n ,2);
      }
      T += n;
      int flow = DINIC(S ,T ,n + n);
      if(flow == 0) printf("%d\n" ,n);
      else if(flow == 2) puts("2");
      else printf("%d\n" ,find(n ,S ,T));
   }
   return 0;
}

思路:
   (2)最短路,先跑一个最短路,记录路径,如果到不了T,那么就输出n,如果能的话,来一个深搜,看看只跑非最短路上的点能不能到达T,如果能,那么就说明至少存在两条不相交的路,那么直接输出2,否则就是存在关键点的情况了,枚举每一个关键点,通过非最短路上的点找到里关键点最远的那个最短路上的点,那么这个点一定是关键点,然后在吧当前的这个点当下一步的关键点,就这样一直找到T就行了..比最大流的那个好写,思路都差不多..
当前点a的下一个关键路径是c,是最远的那一个,如图.

#include<stdio.h>
#include<string.h>
#include<queue>

#define N_node 110000
#define N_edge 330000
#define INF 1000000000

using namespace std;

typedef struct
{
   int to ,next ,cost;
}STAR;

STAR E[N_edge];
int list[N_node] ,tot;
int mer[N_node] ,S ,T;
int s_x[N_node] ,mk_sx[N_node];
int mark[N_node];

void add(int a ,int b ,int c)
{
   E[++tot].to = b;
   E[tot].cost = c;
   E[tot].next = list[a];
   list[a] = tot;
}

bool SPFA(int s ,int t ,int n)
{
   memset(mark ,0 ,sizeof(mark));
   for(int i = 0 ;i <= n ;i ++)
   {
      s_x[i] = INF;
      mer[i] = i;
   }
   s_x[s] = 0;
   mark[s] = 1;
   queue<int>q;
   q.push(s);
   while(!q.empty())
   {
      int xin ,tou;
      tou = q.front();
      q.pop();
      mark[tou] = 0;
      for(int k = list[tou] ;k ;k = E[k].next)
      {
         xin = E[k].to;
         if(s_x[xin] > s_x[tou] + E[k].cost)
         {
            s_x[xin] = s_x[tou] + E[k].cost;
            mer[xin] = tou;
            if(!mark[xin])
            {
               mark[xin] = 1;
               q.push(xin);
            }
         }
      }
   }
   return s_x[t] != INF;
}

int ok;
void DFS_1(int s)
{
   for(int k = list[s] ;k ;k = E[k].next)
   {
      int to = E[k].to;
      if(mark[to]|| ok) continue;
      if(to == T) ok = 1;
      if(mk_sx[to] || ok) continue;
      mark[to] = 1;
      DFS_1(to);
   }
}

int mk_id ,maxx;
void DFS_2(int s)
{
   for(int k = list[s] ;k ;k = E[k].next)
   {
      int to = E[k].to;
      if(mark[to]) continue;
      if(mk_sx[to])
      {
         if(maxx < s_x[to])
         {
            maxx = s_x[to];
            mk_id = to;
         }
        continue ;
      }
      mark[to] = 1;
      DFS_2(to);
   }
}

int main ()
{
   int n ,m ,i ,j;
   int a ,b;
   while(~scanf("%d %d" ,&n ,&m))
   {
      memset(list ,0 ,sizeof(list));
      tot = 1;
      for(i = 1 ;i <= m ;i ++)
      {
         scanf("%d %d" ,&a ,&b);
         add(a + 1 ,b + 1 ,1);
      }
      scanf("%d %d" ,&S ,&T);
      S ++ ,T ++;
      if(!SPFA(S ,T ,n))
      {
         printf("%d\n" ,n);
         continue;
      }
      memset(mk_sx ,0 ,sizeof(mk_sx));
      int now = T;
      while(mer[now] != now)
      {
         mk_sx[now] = 1;
         now = mer[now];
      }
      mk_sx[now] = 1;
      ok = 0;
      memset(mark ,0 ,sizeof(mark));
      mark[S] = 1;
      DFS_1(S);
      if(ok)
      {
         puts("2");
         continue;
      }
      int sum = 1;
      memset(mark ,0 ,sizeof(mark));
      while(1)
      {
         //mk_id ,maxx
         maxx = 0;
         mark[S] = 1;
         DFS_2(S);
         sum ++;
         S = mk_id;
         //printf("%d***\n" ,S);
         if(S == T)  break;
      }
      printf("%d\n" ,sum);
   }
   return 0;
}