删除列Table.RemoveColumns（Power Query 之 M 语言）

数据源：

　　“姓名”“基数”“个人比例”“个人缴纳”“公司比例”“公司缴纳”“总计”，共七列

目标：

　　将其中的“基数”“个人比例” “公司比例”三列删除

操作过程：

　　选取指定列》【主页】》【删除列】

　　

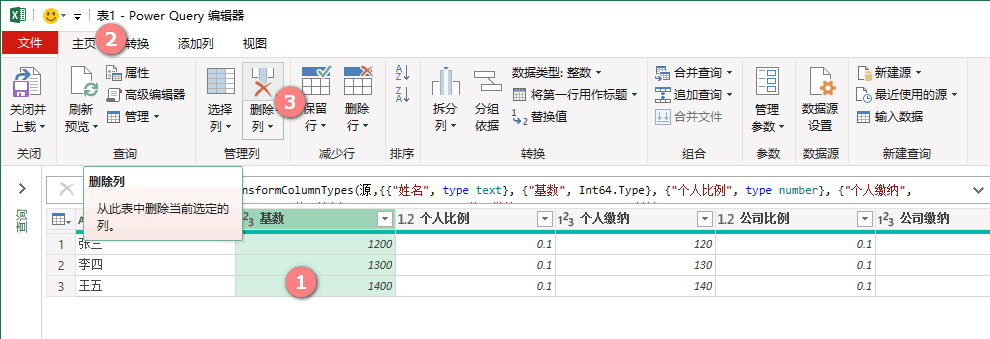
M公式：

　　= Table.RemoveColumns( 表, {"待删除列名1", "待删除列名2", ...,"待删除列名n" }, 处理不存在列)

说明：

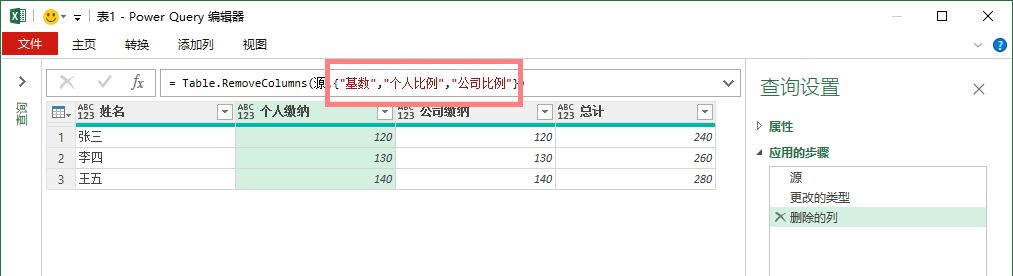
　　表可以在公式中列出，也可以是步骤名，一般默认为上一步步骤，即将由上一步操作完成后所生成的查询表，现实中可以根据实际需求指定步骤。如下图所示，步骤名是“源”步骤，即对由“源”步骤所生成的查询表中“基数”列的删除（现实中尽量使用上一步步骤名）。

　　

　　列名外需要加一对半角的双引号。

　　待删除的列如果不止一列时，可以添加多列，用一对半角的大括号将多列的列名一一列出，并以半角逗号分隔。大括号用于1-N列。

　　

　　当第二参数中的列名不存在时，会出错，这时可以添加上第三参数：

　　　　0：代表MissingField.Error

　　　　1：代表 MissingField.Ignore

　　　　2：代表 MissingField.UseNull

 最终效果：

　　查询表只剩4列了……

扩展：

删除…Remove…