源码解析C#中PriorityQueue(优先级队列)的实现

前言

前段时间看到有大佬对.net 6.0新出的PriorityQueue(优先级队列)数据结构做了解析，但是没有源码分析，所以本着探究源码的心态，看了看并分享出来。它不像普通队列先进先出(FIFO)，而是根据优先级出队。

ps:读者多注意代码的注释。

D叉树的认识(d-ary heap)

首先我们在表示一个堆(大顶堆或小顶堆)的时候，实际上是通过一个一维数组来维护一个二叉树(d=2,d表示每个父节点最多有几个子节点)，首先看下图的二叉树，数字代表索引：

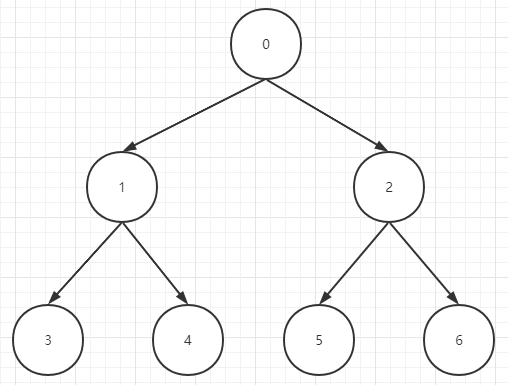
• 任意一个节点的父节点的索引为：(index - 1) / d
• 任意一个节点的左子节点的索引为：(index * d) + 1
• 任意一个节点的右子节点的索引为：(index * d) + 2
• 它的时间复杂度为O(logndn)
  
  通过以上公式，我们就可以轻松通过一个数组来表达一个堆，只需保证能拿到正确的索引即可进行快速的插入和删除。

源码解析

构造初始化

关于这部分主要介绍关键的字段和方法，比较器的初始化以及堆的初始化，请看如下代码：

public class PriorityQueue<TElement, TPriority>
{
    /// <summary>
    /// 保存所有节点的一维数组且每一项是个元组
    /// </summary>
    private (TElement Element, TPriority Priority)[] _nodes;

    /// <summary>
    /// 优先级比较器，这里用的泛型，比较器可以自己实现
    /// </summary>
    private readonly IComparer<TPriority>? _comparer;

    /// <summary>
    /// 当前堆的大小
    /// </summary>
    private int _size;

    /// <summary>
    /// 版本号
    /// </summary>
    private int _version;

    /// <summary>
    /// 代表父节点最多有4个子节点，也就是d=4(d=4时好像效率最高)
    /// </summary>
    private const int Arity = 4;

    /// <summary>
    /// 使用位运算符，表示左移2或右移2(效率更高)，即相当于除以4，
    /// </summary>
    private const int Log2Arity = 2;

    /// <summary>
    ///  构造函数初始化堆和比较器
    /// </summary>
    public PriorityQueue()
    {
        _nodes = Array.Empty<(TElement, TPriority)>();
        _comparer = InitializeComparer(null);
    }

    /// <summary>
    ///  重载构造函数，来定义比较器否则使用默认的比较器
    /// </param>
    public PriorityQueue(IComparer<TPriority>? comparer)
    {
        _nodes = Array.Empty<(TElement, TPriority)>();
        _comparer = InitializeComparer(comparer);
    }
    private static IComparer<TPriority>? InitializeComparer(IComparer<TPriority>? comparer)
    {
        //如果是值类型，如果是默认比较器则返回null
        if (typeof(TPriority).IsValueType)
        {
            if (comparer == Comparer<TPriority>.Default)
            {
                return null;
            }

            return comparer;
        }
        //否则就使用自定义的比较器
        else
        {
            return comparer ?? Comparer<TPriority>.Default;
        }
    }

    /// <summary>
    /// 获取索引的父节点
    /// </summary>
    private int GetParentIndex(int index) => (index - 1) >> Log2Arity;

    /// <summary>
    /// 获取索引的左子节点
    /// </summary>
    private int GetFirstChildIndex(int index) => (index << Log2Arity) + 1;
}

单元总结：

1. 实际所有元素使用一维数组来维护这个堆。
2. 调用方可以自定义比较器，但是类型得一致。 如果没有比较器，则使用默认的比较器。
3. 默认一个父节点最多有4个子节点，D=4时效率好像是最好的。
4. 获取父节点索引位置和子节点索引位置使用位运算符，效率更高。

入队操作

入队操作操作相对简单，主要是做扩容和插入处理，请看如下代码：

public void Enqueue(TElement element, TPriority priority)
{
    //拿到最大位置的索引，然后再将数组长度+1
    int currentSize = _size++;
    _version++;
    //如果长度相等，说明已经到达最大位置，数组需要扩容了才能容下更多的元素
    if (_nodes.Length == currentSize)
    {
        //扩容,参数是代表数组最小容量
        Grow(currentSize + 1);
    }

    if (_comparer == null)
    {

        MoveUpDefaultComparer((element, priority), currentSize);
    }
    else
    {
        MoveUpCustomComparer((element, priority), currentSize);
    }
}
private void Grow(int minCapacity)
{
    //增长倍数
    const int GrowFactor = 2;
    //每次扩容的最小值
    const int MinimumGrow = 4;
    //每次扩容都2倍扩容
    int newcapacity = GrowFactor * _nodes.Length;

    //数组不能大于最大长度
    if ((uint)newcapacity > Array.MaxLength) newcapacity = Array.MaxLength;

    //使用他们两个的最大值
    newcapacity = Math.Max(newcapacity, _nodes.Length + MinimumGrow);

    //如果比参数小，则使用参数的最小值
    if (newcapacity < minCapacity) newcapacity = minCapacity;
    //重新分配内存，设置大小，因为数组的保存在内存中是连续的
    Array.Resize(ref _nodes, newcapacity);
}
private void MoveUpDefaultComparer((TElement Element, TPriority Priority) node, int nodeIndex)
{
    //nodes保存副本
    (TElement Element, TPriority Priority)[] nodes = _nodes;
    //这里入队操作是从空闲索引第一个位置开始插入
    while (nodeIndex > 0)
    {
        //找父节点索引位置
        int parentIndex = GetParentIndex(nodeIndex);
        (TElement Element, TPriority Priority) parent = nodes[parentIndex];
        //插入节点和父节点比较，如果小于0(默认比较器情况下构建的小顶堆)，则交换位置
        if (Comparer<TPriority>.Default.Compare(node.Priority, parent.Priority) < 0)
        {
            nodes[nodeIndex] = parent;
            nodeIndex = parentIndex;
        }
        //算是性能优化吧，不必检查所有节点，当发现大于时，就直接退出就可以了
        else
        {
            break;
        }
    }
    //将插入节点放到它应该的位置
    nodes[nodeIndex] = node;
}

单元总结：

1. 首先记录当前元素最大的索引位置，根据适当的情况来扩容。
2. 扩容正常情况下是以2倍的增长速度扩容。
3. 插入数据时，从最后一个节点的父节点向上还是找，比较元素的Priority，交换位置，默认情况下是构建小顶堆。

出队操作

出队操作简单来说就是将根元素返回并移除(也就是数组的第一个元素)，然后根据比较器将最小或最大的元素放到堆顶，请看如下代码：

public TElement Dequeue()
{
    if (_size == 0)
    {
        throw new InvalidOperationException(SR.InvalidOperation_EmptyQueue);
    }
    //将堆顶元素返回
    TElement element = _nodes[0].Element;
    //然后调整堆
    RemoveRootNode();
    return element;
}
private void RemoveRootNode()
{
    //记录最后一个元素的索引位置，并且将堆的大小-1
    int lastNodeIndex = --_size;
    _version++;

    if (lastNodeIndex > 0)
    {
        //堆的大小已经被减1，所以将最后一个元素作为副本，开始从堆顶重新整理堆
        (TElement Element, TPriority Priority) lastNode = _nodes[lastNodeIndex];
        if (_comparer == null)
        {
            MoveDownDefaultComparer(lastNode, 0);
        }
        else
        {
            MoveDownCustomComparer(lastNode, 0);
        }
    }

    if (RuntimeHelpers.IsReferenceOrContainsReferences<(TElement, TPriority)>())
    {
        //将最后一个位置的元素设置为默认值
        _nodes[lastNodeIndex] = default;
    }
}
private void MoveDownDefaultComparer((TElement Element, TPriority Priority) node, int nodeIndex)
{
    (TElement Element, TPriority Priority)[] nodes = _nodes;
    //堆的实际大小
    int size = _size;

    int i;
    //当左子节点的索引小于堆的实际大小时
    while ((i = GetFirstChildIndex(nodeIndex)) < size)
    {
        //左子节点元素
        (TElement Element, TPriority Priority) minChild = nodes[i];
        //当前左子节点的索引
        int minChildIndex = i;
        //这里即找到所有同一个父节点的相邻子节点，但是要判断是否超出了总的大小
        int childIndexUpperBound = Math.Min(i + Arity, size);
        //按照索引区间顺序查找，并根据比较器找到最小的子元素位置
        while (++i < childIndexUpperBound)
        {
            (TElement Element, TPriority Priority) nextChild = nodes[i];
            if (Comparer<TPriority>.Default.Compare(nextChild.Priority, minChild.Priority) < 0)
            {
                minChild = nextChild;
                minChildIndex = i;
            }
        }
        //如果最后一个节点的元素，比这个最小的元素还小，那么直接放到父节点即可
        if (Comparer<TPriority>.Default.Compare(node.Priority, minChild.Priority) <= 0)
        {
            break;
        }
        //将最小的子元素赋值给父节点
        nodes[nodeIndex] = minChild;
        nodeIndex = minChildIndex;
    }
    //将最后一个节点放到空闲出来的索引位置
    nodes[nodeIndex] = node;
}

单元总结：

1. 返回根节点元素，然后移除根节点元素，调整堆。
2. 从根节点开始，依次查找对应父节点的所有子节点，放到堆顶，也就是数组索引0的位置，然后如果树还有层数，继续循环查找。
3. 将最后一个元素放到堆适当的位置，然后再将最后一个位置的元素置为默认值。

总结

通过源码的解读，除了了解类的设计之外，更对对优先级队列数据结构的实现有了更加深刻和清晰的认识。

这里也只是粘贴出主要的代码，需要看详细代码的请点击这里，笔者可能有一些解读错误的地方，欢迎评论指正。