[Luogu] 次小生成树

https://www.luogu.org/problemnew/show/P4180#sub

严格次小生成树，即不等于最小生成树中的边权之和最小的生成树

首先求出最小生成树，然后枚举所有不在最小生成树里的边，找出最小增量，

如果将一条不在最小生成树里的边加入生成树，那么就会形成环

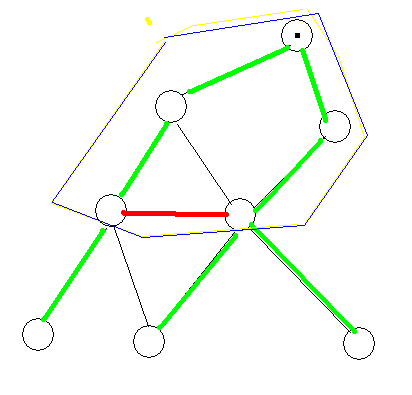
如图，绿色为最小生成树，如果将红色边加入，就在紫色区域构成了环

那么现在增量就是用红色边的边权 - 紫色区域内最大的绿色边的边权
这里红色边的边权一定大于等于紫色区域内最大的绿色边的边权（由最小生

成树的构成可知），如果红色边的边权 = 紫色区域内最大的绿色边的边权

那么紫色区域就要取次大值（因为要求严格次小）

套路：将这个环分成 lca (红色边的u，v的lca) 到 u 和 lca 到 v 两条路径

倍增最大值和次大值即可

Answer = 最小生成树 + 最小增量

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>

using namespace std;
const int N = 1e5 + ;

#define gc getchar()

int n, m, now = ;
struct Node {
    int u, v, w, is_in;
    bool operator <(const Node a)const {
        return w < a.w;
    }
} E[N * ];
struct Node_2{int u, v, w, nxt;} G[(N * ) << ];
int fa[N][], Max[N][], Tmax[N][], deep[N], head[N], father[N];
int Mi[];

#define LL long long
LL Answer; int Min = 1e9;

inline int read() {
    int x = ; char c = gc;
    while(c < '' || c > '') c = gc;
    while(c >= '' || c >= '') x = x *  + c - '', c = gc;
    return x;
}

void Add(int u, int v, int w) {G[now].v = v; G[now].w = w; G[now].nxt = head[u]; head[u] = now ++;}
int Getfa(int x) {return father[x] == x ? x : father[x] = Getfa(father[x]);}

void Mst() {
    int js();
    for(int i = ; js != n - ; i ++) {
        int u = E[i].u, v = E[i].v, fu = Getfa(u), fv = Getfa(v);
        if(fu != fv) {
            father[fu] = fv;
            js ++;
            E[i].is_in = ;
            Answer += (LL)E[i].w;
            Add(E[i].u, E[i].v, E[i].w);
            Add(E[i].v, E[i].u, E[i].w);
        }
    }
}

void Dfs(int x, int f_, int dep) {
    deep[x] = dep;
    for(int i = ; ; i ++) {
        if(deep[x] - Mi[i] < ) break;
        fa[x][i] = fa[fa[x][i - ]][i - ];
        Max[x][i] = max(Max[x][i - ], Max[fa[x][i - ]][i - ]);
        if(Max[x][i - ] == Max[fa[x][i - ]][i - ])
            Tmax[x][i] = max(Tmax[x][i - ], Tmax[fa[x][i - ]][i - ]);
        else
            Tmax[x][i] = max(min(Max[x][i - ], Max[fa[x][i - ]][i - ]),
                         max(Tmax[x][i - ], Tmax[fa[x][i - ]][i - ]));
    }
    for(int i = head[x]; ~ i; i = G[i].nxt) {
        int v = G[i].v;
        if(v != f_) {fa[v][] = x; Max[v][] = G[i].w; Tmax[v][] = -; Dfs(v, x, dep + );}
    }
}

int Lca(int x, int y) {
    if(deep[x] < deep[y]) swap(x, y);
    int k = deep[x] - deep[y];
    for(int i = ; i <=  ; i ++)
        if(k >> i & ) x = fa[x][i];
    if(x == y) return x;
    for(int i = ; i >= ; i --)
        if(fa[x][i] != fa[y][i]) x = fa[x][i], y = fa[y][i];
    return fa[x][];
}

void Work(int s, int t, int w_) {
    int m1 = , m2 = , k = deep[s] - deep[t];
    for(int i = ; i <= ; i ++) {
        if(k >> i & ) {
            m2 = max(m2, Tmax[s][i]);
            if(Max[s][i] > m1) {m2 = max(m2, m1); m1 = Max[s][i];}
        }
    }
    if(m1 == w_) Min = min(Min, w_ - m2);
    else Min = min(Min, w_ - m1);
}

int main() {
    n = read(); m = read();
    for(int i = ; i <= n; i ++) head[i] = -, father[i] = i;
    Mi[] = ;
    for(int i = ; i <= ; i ++) Mi[i] = Mi[i - ] * ;
    for(int i = ; i <= m; i ++) {E[i].u = read(), E[i].v = read(), E[i].w = read();}
    sort(E + , E + m + );
    Mst();
    Dfs(, , );
    for(int i = ; i <= m; i ++) {
        if(!E[i].is_in) {
            int u = E[i].u, v = E[i].v;
            int L = Lca(u, v);
            Work(u, L, E[i].w);
            Work(v, L, E[i].w);
        }
    }
    cout << Answer + Min;
    return ;
}

树剖版，cogs AC，luogu 80

线段树维护区间最大和严格次大

/*
    次小生成树的链剖实现
*/
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>

using namespace std;
const int N = 1e5 + ;

#define gc getchar()
#define LL long long

int n, m, now = , Tim, Min = (int)1e9, Max1, Max2;
int head[N], deep[N], top[N], fa[N], tree[N], bef[N], size[N], son[N], dad[N], data[N];
int Max[N << ], Tmax[N << ];
struct Node {
    int u, v, w, is_in;
    bool operator <(const Node a) const {return w < a.w;}
}E[N << ];
struct Node_2{int u, v, w, nxt;} G[N << ];
LL Answer;

inline int read() {
    int x = ; char c = gc;
    while(c < '' || c > '') c = gc;
    while(c >= '' || c >= '') x = x *  + c - '', c = gc;
    return x;
}

void Add(int u, int v, int w) {G[now].u = u; G[now].v = v; G[now].w = w; G[now].nxt = head[u]; head[u] = now ++;}
int Getfa(int x) {return dad[x] == x ? x : dad[x] = Getfa(dad[x]);}

void Dfs_find_son(int u, int f_, int dep) {
    fa[u] = f_;
    deep[u] = dep;
    size[u] = ;
    for(int i = head[u]; ~ i; i = G[i].nxt) {
        int v = G[i].v;
        if(v != f_) {
            data[v] = G[i].w;
            Dfs_find_son(v, u, dep + );
            size[u] += size[v];
            if(size[v] > size[son[u]]) son[u] = v;
        }
    }
}

void Dfs_un(int u, int tp) {
    top[u] = tp;
    tree[u] = ++ Tim;
    bef[Tim] = u;
    if(!son[u]) return ;
    Dfs_un(son[u], tp);
    for(int i = head[u]; ~ i; i = G[i].nxt) {
        int v = G[i].v;
        if(v != fa[u] && v != son[u]) Dfs_un(v, v);
    }
}

void Mst() {
    int js();
    for(int i = ; js != n - ; i ++) {
        int u = E[i].u, v = E[i].v, fu = Getfa(u), fv = Getfa(v);
        if(fu != fv) {
            dad[fu] = fv; js ++; E[i].is_in = ; Answer += (LL)E[i].w;
            Add(E[i].u, E[i].v, E[i].w); Add(E[i].v, E[i].u, E[i].w);
        }
    }
}

#define lson jd << 1
#define rson jd << 1 | 1 

void Push_up(int jd) {
    if(Max[lson] == Max[rson]) {
        Max[jd] = Max[lson];
        Tmax[jd] = max(Tmax[lson], Tmax[rson]);
    } else {
        Max[jd] = max(Max[lson], Max[rson]);
        Tmax[jd] = max(min(Max[lson], Max[rson]), max(Tmax[lson], Tmax[rson]));
    }
}

void Build_tree(int l, int r, int jd) {
    if(l == r) {
        Max[jd] = data[bef[l]];
        Tmax[jd] = -;
        return ;
    }
    int mid = (l + r) >> ;
    Build_tree(l, mid, lson);
    Build_tree(mid + , r, rson);
    Push_up(jd);
}

int Lca(int x, int y) {
    int tp1 = top[x], tp2 = top[y];
    while(tp1 != tp2) {
        if(deep[tp1] < deep[tp2]) swap(x, y), swap(tp1, tp2);
        x = fa[tp1];
        tp1 = top[x];
    }
    return deep[x] < deep[y] ? x : y;
}

void Sec_G(int l, int r, int jd, int x, int y) {
    if(x <= l && r <= y) {
        if(Max[jd] > Max1) {Max2 = max(Max1, Tmax[jd]); Max1 = Max[jd];}
        else if(Max[jd] == Max1) Max2 = max(Max2, Tmax[jd]);
        else Max2 = max(Max2, Max[jd]);
        return ;
    }
    int mid = (l + r) >> ;
    if(x <= mid) Sec_G(l, mid, lson, x, y);
    if(y > mid)  Sec_G(mid + , r, rson, x, y);
}

void Sec_G_imp(int x, int y, int w_) {
    int tp1 = top[x], tp2 = top[y], M1 = , M2 = ;
    while(tp1 != tp2) {
        if(deep[tp1] < deep[tp2]) swap(x, y), swap(tp1, tp2);
        Max1 = , Max2 = ;
        Sec_G(, n, , tree[tp1], tree[x]);
        if(Max1 > M1) {M2 = max(M1, Max2), M1 = Max1;}
        else if(Max1 == M1) M2 = max(M2, Max2);
        else M2 = max(M2, Max1);
        x = fa[tp1]; tp1 = top[x];
    }
    if(x == y) return ;
    if(deep[x] < deep[y]) swap(x, y);
    Max1 = , Max2 = ;
    Sec_G(, n, , tree[y] + , tree[x]);
    if(Max1 > M1) {M2 = max(M1, Max2), M1 = Max1;}
    else if(Max1 == M1) M2 = max(M2, Max2);
    else M2 = max(M2, Max1);
    if(M1 == w_) Min = min(Min, w_ - M2);
    else Min = min(Min, w_ - M1);
}

int main() {
    n = read(), m = read();
    for(int i = ; i <= n; i ++) dad[i] = i, head[i] = -;
    for(int i = ; i <= m; i ++) {E[i].u = read(), E[i].v = read(), E[i].w = read();}
    sort(E + , E + m + );
    Mst();
    Dfs_find_son(, , );
    Dfs_un(, );
    Build_tree(, n, );
    for(int i = ; i <= m; i ++){
        if(!E[i].is_in) {
            int u = E[i].u, v = E[i].v;
            Sec_G_imp(u, v, E[i].w);
        }
    }
    std:: cout << Answer + Min;
    return ;
}