页面某些特定图标的权限，比如导入导出表格，下载等等，这个权限必须在有某个页面查看的权利的基础上（细粒度）（shiro项目中来的四）

一，查找按钮权限的设置

第一步：会根据用户的相关信息去查到它的角色表；

SELECT * FROM SYS_USER WHERE user_id='eded77bdf35347249b2bacfa181c869d'

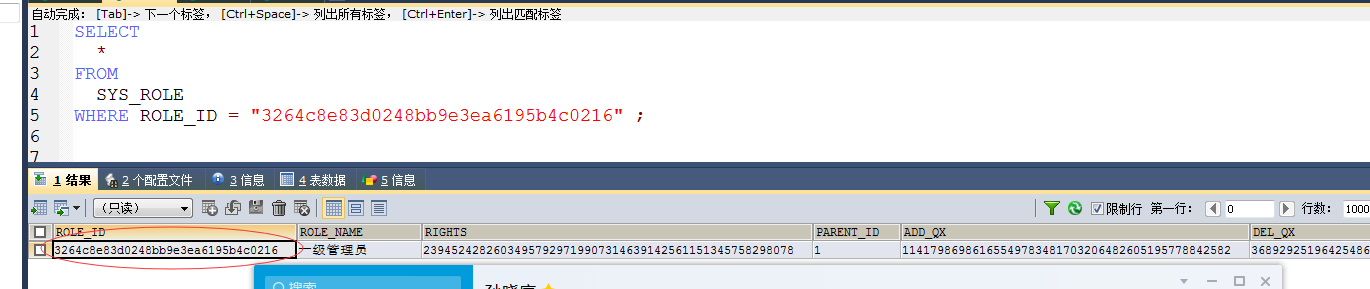
第二步：有了角色表之后再根据角色与权限的中间表查到权限表相关的信息；
buttonQXnamelist = buttonrightsService.listAllBrAndQxname(ROLE_ID); //此角色拥有的按钮权限标识列表
SELECT
*
FROM
SYS_ROLE_FHBUTTON a
LEFT JOIN SYS_FHBUTTON b
ON a.BUTTON_ID = b.FHBUTTON_ID
WHERE a.ROLE_ID = '68f8e4a39efe47c7bb869e9d15ab925d'

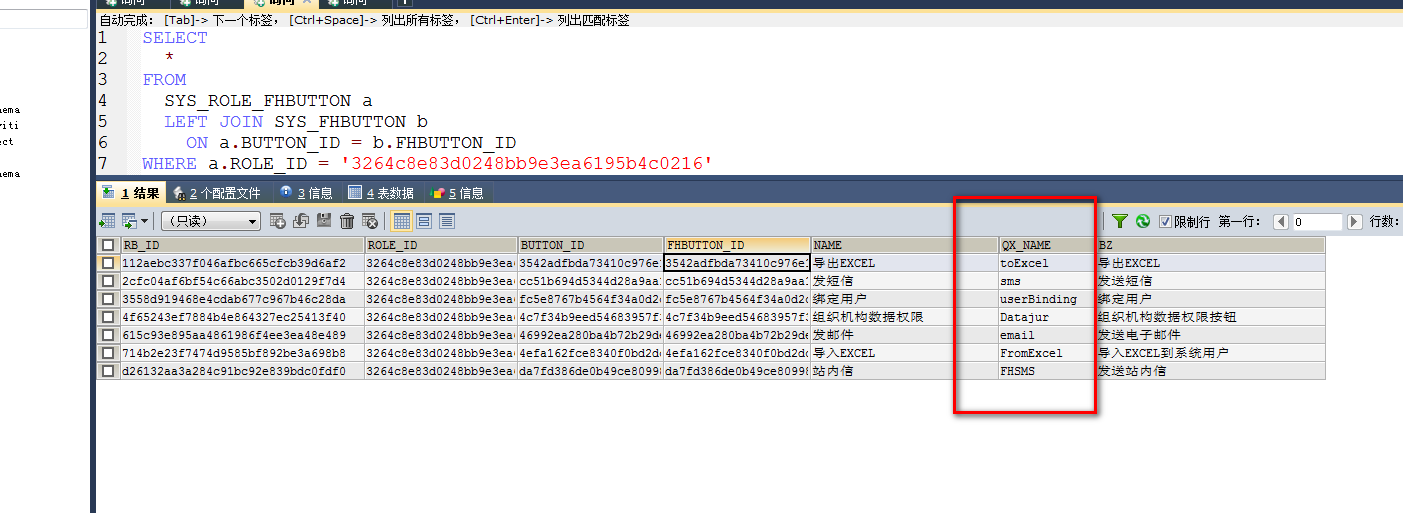
第三步，假如权限表中有这个权限则取它的名字，并把它的值设置成1；
map.put(buttonQXnamelist.get(i).getString("QX_NAME"),"1"); //按钮权限
{Datajur=1, email=1, FromExcel=1, toExcel=1, userBinding=1, sms=1, FHSMS=1}
第四步：假如以后有权限的修改直接来增加或者删除角色与权限的中间表就行了，其它的不用动。

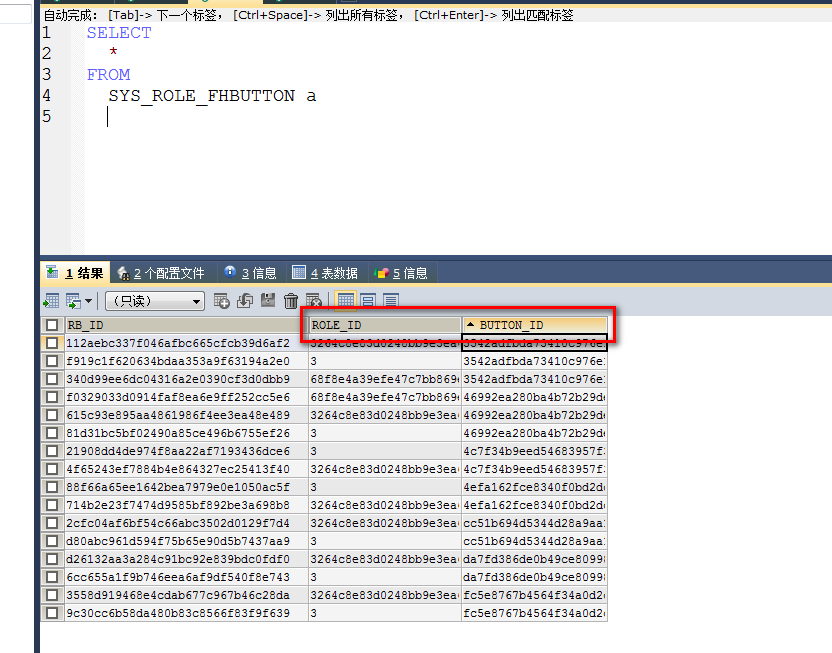
二，当跳出页面的逻辑

onclick=siMenu('m37','z2','按钮权限','buttonrights/list.do')主要就是把角色表的信息，角色与权限的中间表的信息，和权限表的信息传到前台就行了。
SYS_ROLE张表中有所有的角色
SYS_ROLE_FHBUTTON 是角色与权限的中间表
SYS_FHBUTTON 权限表
SYS_ROLE.ROLE_ID=SYS_ROLE_FHBUTTON.ROLE_ID&&SYS_FHBUTTON.FHBUTTON_ID=SYS_ROLE_FHBUTTON.BUTTON_ID

SELECT t.*,h.* FROM SYS_ROLE t,SYS_ROLE_FHBUTTON h WHERE t.ROLE_ID=h.ROLE_ID

SELECT t.*,h.* FROM SYS_FHBUTTON t,SYS_ROLE_FHBUTTON h WHERE SYS_FHBUTTON.FHBUTTON_ID=SYS_ROLE_FHBUTTON.BUTTON_ID;

三，点击按钮时候时候的逻辑

这时候如果去除某个角色的某个权限，只需要把中间表的ROLE_ID ，和中间表的BUTTON_ID删除就行了，这就断掉了两者之间的联系就没有这个权限了。
url: "http://localhost:8088/MVNFHM/buttonrights/upRb.do?ROLE_ID="+ROLE_ID+"&BUTTON_ID="+FHBUTTON_ID+"&guid="+new Date().getTime(),
如果没有就添加，如果有就删除
这个表：SYS_ROLE_FHBUTTON
BUTTON_ID ROLE_ID 主要是这两个字段
if(null != buttonrightsService.findById(pd)){ //判断关联表是否有数据 是:删除/否:新增
buttonrightsService.delete(pd); //删除
FHLOG.save(Jurisdiction.getUsername(), "删除按钮权限"+pd);
}else{
pd.put("RB_ID", this.get32UUID()); //主键
buttonrightsService.save(pd); //新增