逻辑回归&线性支持向量机

代码：

 # -*- coding: utf-8 -*-
 """
 Created on Tue Jul 17 10:13:20 2018

 @author: zhen
 """

 from sklearn.linear_model import LogisticRegression
 from sklearn.svm import LinearSVC
 import mglearn
 import matplotlib.pyplot as plt

 x, y = mglearn.datasets.make_forge()

 fig, axes = plt.subplots(1, 2, figsize=(10,3))
 # 线性支持向量机与逻辑回归进行比较
 for model, ax in zip([LinearSVC(), LogisticRegression()], axes):
     clf = model.fit(x, y)
     mglearn.plots.plot_2d_separator(clf, x, fill=False, eps=0.5, ax=ax, alpha=0.7)
     mglearn.discrete_scatter(x[:, 0], x[:, 1], y, ax=ax)
     ax.set_title("{}".format(clf.__class__.__name__))
     ax.set_xlabel("Feature 0")
     ax.set_ylabel("Feature 1")
 axes[0].legend()

 #
 from sklearn.datasets import load_breast_cancer
 from sklearn.model_selection import train_test_split
 cancer = load_breast_cancer()

 x_train, x_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42)
 # 使用默认配置参数
 log_reg = LogisticRegression().fit(x_train, y_train)

 print("="*25+"逻辑回归（C=1）"+"="*25)
 print("Training set score：{:.3f}".format(log_reg.score(x_train, y_train)))
 print("Test set score：{:.3f}".format(log_reg.score(x_test, y_test)))

 # 使用配置参数C=100
 log_reg_100 = LogisticRegression(C=100).fit(x_train, y_train)

 print("="*25+"逻辑回归（C=100）"+"="*25)
 print("Training set score：{:.3f}".format(log_reg_100.score(x_train, y_train)))
 print("Test set score：{:.3f}".format(log_reg_100.score(x_test, y_test)))

 # 使用配置参数C=0.01
 log_reg_001 = LogisticRegression(C=0.01).fit(x_train, y_train)

 print("="*25+"逻辑回归（C=0.01）"+"="*25)
 print("Training set score：{:.3f}".format(log_reg_001.score(x_train, y_train)))
 print("Test set score：{:.3f}".format(log_reg_001.score(x_test, y_test)))
 print("="*25+"逻辑回归&线性支持向量机"+"="*25)
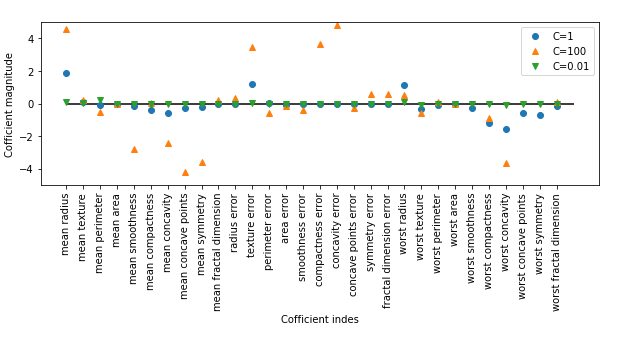
 # 可视化
 fig, axes = plt.subplots(1, 1, figsize=(10,3))
 plt.plot(log_reg.coef_.T, 'o', label="C=1")
 plt.plot(log_reg_100.coef_.T, '^', label="C=100")
 plt.plot(log_reg_001.coef_.T, 'v', label="C=0.01")
 plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)
 plt.hlines(0, 0, cancer.data.shape[1])

 plt.ylim(-5, 5)

 plt.xlabel("Cofficient indes")
 plt.ylabel("Cofficient magnitude")

 plt.legend()

结果：