[测试题]line

Description

Input

Output

Sample Input

10 4974
3636 3
6679 70
7182 93
10618 98
14768 23
15242 99
16077 35
23368 46
27723 15
32404 81

Sample Output

0.465308

Hint

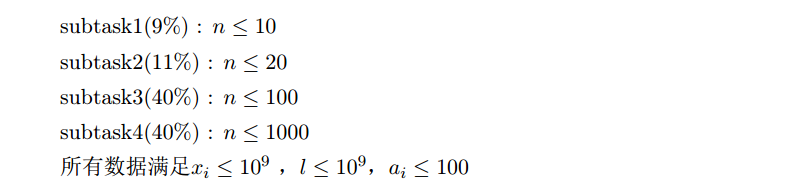
题解

典型的 $01$ 分数规划。

我们假设 $x[]$ 中和 $a[]$ 中只保存了选取的点。

依题，要求 $$ans={{\sum_i {\sqrt{|x[i]-x[i-1]-l|}}} \over {\sum_i a[i]}}$$

按照 $01$ 分数规划的套路，我们假设有对于当前值更优的解。

$$\begin{aligned}ans&\geq{{\sum_i {\sqrt{|x[i]-x[i-1]-l|}}} \over {\sum_i a[i]}}\\ans\times{\sum_i a[i]}&\geq{\sum_i {\sqrt{|x[i]-x[i-1]-l|}}}\\{\sum_i ({ans\times a[i]})}&\geq{\sum_i {\sqrt{|x[i]-x[i-1]-l|}}}\\0&\geq{\sum_i {\sqrt{|x[i]-x[i-1]-l|}}}-{\sum_i ({ans\times a[i]})}\\0&\geq{\sum_i ({\sqrt{|x[i]-x[i-1]-l|}-ans\times a[i]})}\end{aligned}$$

那么我们去二分这个 $ans$，每次做一次 $\text{DP}$ 判断有无更优解即可。

 //It is made by Awson on 2017.9.19
 #include <map>
 #include <set>
 #include <cmath>
 #include <ctime>
 #include <queue>
 #include <stack>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 #define LL long long
 #define Max(a, b) ((a) > (b) ? (a) : (b))
 #define Min(a, b) ((a) < (b) ? (a) : (b))
 #define Abs(a) ((a) < 0 ? (-(a)) : (a))
 #define lowbit(x) ((x)&(-(x)))
 using namespace std;
 const int INF = ~0u>>;
 const int N = ;
 const double eps = 1e-;
 
 int n, l;
 int x[N+], a[N+];
 
 bool judge(double r) {
     double f[N+];
     f[] = ;
     for (int i = ; i <= n; i++) {
         f[i] = INF;
         for (int j = ; j < i; j++)
             f[i] = min(f[i], f[j]+sqrt(Abs(x[i]-x[j]-l))-r*a[i]);
     }
     return f[n] < eps;
 }
 void work() {
     for (int i = ; i <= n; i++)
         scanf("%d%d", &x[i], &a[i]);
     double L = , R = 1e9;
     while (R - L > eps) {
         double mid = (L+R)/.;
         if (judge(mid)) R = mid;
         else L = mid;
     }
     printf("%.6lf\n", L);
 }
 
 int main() {
     freopen("line.in", "r", stdin);
     freopen("line.out", "w", stdout);
     while (~scanf("%d%d", &n, &l))
         work();
     return ;
 }